文章目录

1 概率分析与随机算法
2 堆排序

1 概率分析与随机算法

1.1 雇佣问题

假如现在要雇用一名新的办公助理。先前的雇用尝试都失败了，于是公司决定找一个雇用代理。雇用代理每天会推荐一个应聘者。公司面试这个人，然后决定是否雇用他。公司必须付给雇用代理一小笔费用，以便面试应聘者。然而要真的雇用一个应聘者需要花更多的钱，因为公司必须先辞掉目前的办公助理，还要付一大笔中介费给雇用代理。在任何时候，公司都希望找最适合的人来担任这项职务。因此，雇佣代理决定在面试完每个应聘者后，如果该应聘者比目前的办公助理更合适，就会辞掉当前的办公助理，然后聘用新的。公司愿意为该策略付费，但希望雇佣代理能够估算该费用会是多少。

假设应聘办公助理的候选人编号为1到n。该过程中假设雇佣代理能在面试完应聘者i后，决定应聘者i是否是自己目前见过的最佳人选，如果该面试者比前面所有面试者都好，就录用。初始化时，该过程创建一个虚拟的应聘者，编号为0，他比其他所有应聘者都差。下面给出的HireAsssistant的伪代码，以表示该雇用策略：

HireAssistant(n){
    
     //n个候选者
    best=0; //假设候选者0作为初始候选人
    for(i=1;i<=n;i++){
    
    
        interview(candidate i);
        if candidate i is better than candidate best:
            best=i;
            hire(candidate i);
    }
}

已知面试代价为C_i，录用代价为C_h，请问成本为多少?

设m为雇佣人数，则总成本为O(nC_i+mC_h)，最坏情况下是O(nC_i+nC_h)，即按面试者质量增序面试。

因此，需要知道面试者质量的分布。假定：

（1）根据面试者质量的随机序列参加面试；

（2）rank(i)是第i个面试者的质量等级。

下面是雇佣问题成本的概率分析：

设X为随机变量，其值等于雇佣新职员的次数，则期望E[X]为：
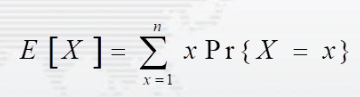
在这里插入图片描述
上图中，Pr{X=x}表示X=x时的概率，其中x=1,2,…,n。记X_i=Ⅰ{candidate i被雇用}，关于Ⅰ{candidate i被雇用}的值，有两种情况：i被雇用时值为1，否则为0。可知X=X₁+X₂+…+X_n，且E[X_i]=Pr{candidate i被雇用}=1/i，则有：
在这里插入图片描述
上图用到了调和级数，对于正整数n，第n个调和数是：

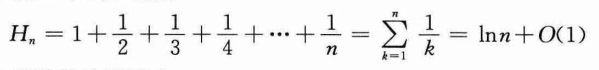
强调面试者质量的分布必须是均匀随机分布，因为特定面试者质量分布的实际成本与期望成本可能有很大差别，举3个例子：

（1）rank={1,2,3,…,10}，则雇佣人数m=n=10，即雇佣面试的所有应聘者；

（2）rank={10,9,…,1}，则雇佣人数m=1，即雇佣面试排名为10的应聘者；

（3）rank={5,2,1,8,4,7,10,9,3,6}，则雇佣人数m=3，即雇佣面试排名为5、8和10的3位应聘者。

给定输入实例，算法每次执行的结果一定相同；但是给定输入，算法多次运行的结果不一定相同。这里强调了输入与输入实例的区别：后者规定了输入的顺序，前者不管输入顺序。举个栗子，输入为{1,2,3,4,5}，输入实例可以为{5,4,3,2,1}或{1,4,2,5,3}或{2,4,1,5,3}等等，后面三个实例的输入均为{1,2,3,4,5}，因此只说输入时对应的输入实例有多种，因此给定输入，算法多次运行的结果不一定相同。而指定了输入顺序的输入实例，算法每次执行的结果一定相同。

1.2 随机算法

1.2.1 随机枚举数组

下面是随机枚举数组的伪代码：

Permute-By-Sorting(A){
    
     //A是一个数组
    n=length(A);
    for(i=1;i<=n;i++)
        P[i]=Random(1,n^3);
    Merge-Sort:sort A, using P as sort keys;
    return A;
}

上述代码中，A[i]是第i个元素，P[i]是第i个元素的优先级，其中每个元素的优先级是随机生成的。举个栗子，输入的数组A={1，2，3，4}，算法生成的优先级数组P={9，27，5，13}，则最后输出为A={3，1，4，2}。

随机枚举数组算法分析：

1）各优先数唯一的概率为1-1/n（我不知道是怎么算的）；

2）算法运行时间为Θ(n·lg n)，这是因为使用了归并排序。

引理：假定各优先数唯一，则Permute-By-Sorting算法产生的是输入的均匀随机排列。证明过程见《算法导论》第三版P71上方。

随机雇佣问题的伪代码如下：

Randomized-Hire-Assistant(n){
    
     //n个候选者
    randomly permute the list of candidates //随机排列候选人名单
    best=0; //假设候选者0作为初始候选人
    for(i=1;i<=n;i++){
    
    
        interview(candidate i);
        if candidate i is better than candidate best:
            best=i;
            hire(candidate i);
    }
}

上述第2行代码事先将候选人名单进行了随机排列。

1.2.2 就地枚举数组

一般就地算法指的是算法使用的辅助空间大小为常数c，与问题规模n无关。就地枚举数组的伪代码如下：

Randomized-In-Place(A){
    
     //A是一个数组
    n=length(A);
    for(i=1;i<=n;i++)
        swap(A[i],A[Random(i,n)]); //交换两个位置的元素
}

就地枚举数组算法的运行时间为Θ(n)，这是因为第3行的循环。上述算法产生的是输入的均匀随机排列。

1.3 在线雇佣问题

原则：面试每位申请者，立即决定去留。

寻找一个平衡点：既要使面试的人数最小化，同时还要使被录用者质量最优。

方法：打分score(i)，并且假定分数唯一，然后选择一个正整数k，对前k个人只记分不录用，此后出现的第一个高分者被录用。若后n-k个人的分数都低于前k个人的最高分数者，就录用第n个人。

在线雇佣问题的伪代码如下：

Online-Maximum(k,n){
    
    
    bestscore=-∞; //刚开始设为-∞
    for(i=1;i<=k;i++)
        if(score(i)>bestscore)
            bestscore=score(i);
    for(i=k+1;i<=n;i++)
        if(score(i)>bestscore)
            return i;
    return n;
}

对每个可能的k，希望确定能雇用最好应聘者的概率，然后选择最佳的k值，并用该值来实现上述雇佣策略。

暂时先假设k是固定的，设：
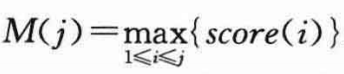
在这里插入图片描述
M(j)表示应聘者1~j中的最高分数。设S表示成功选择到最好应聘者的事件，S_i表示最好的应聘者是第i个面试者时成功的事件。既然不同的S_i不相交，则有：

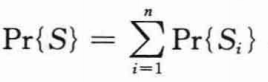
当最好应聘者是前k个应聘者中的某一个时，算法是不会成功的。于是对i=1,2,…,k，有Pr{S_i}=0。因而得到：
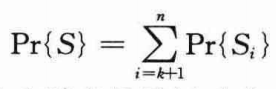
在这里插入图片描述
现在来计算Pr{S_i}。为了使——当第i个应聘者是最好时成功，两件事情必须发生：

（1）最好的应聘者必须在位置i上，用事件B_i表示；

（2）不能选择从位置k+1~i-1中任何一个应聘者，即当k+1<j<i-1时，有score(j)<bestcore。因为分数是唯一的，所以可以忽略score(j)=bestcore的可能性。换句话说，所有score(k+1)到score(i-1)的值都必须小于M(k)；如果其中有大于M(k)的数，则将返回第一个大于M(k)的数的下标。

用O_i表示从位置k+1到i-1中没有任何应聘者入选的事件。幸运的是，两个事件B_i和O_i是彼此独立的。事件O_i仅依赖于位置1到i-1中值的相对次序，而B仅依赖于位置i的值是否大于所有其他位置的值。从位置1到i-1的排序并不影响位置i的值是否大于上述所有值，并且位置i的值也不会影响从位置1到i-1值的次序。因而得到Pr{S_i)=Pr{B_i∩O_i)=Pr{B_i}Pr{O_i)。Pr(B_i}的概率显然是1/n，因为最大值等可能地是n个位置中的任一个。若事件O_i要发生，从位置1到i-1的最大值必须在前k个位置的一个，而最大值等可能地在这i-1个位置中的任一个。于是，Pr{O_i}=k/(i-1)，Pr{S_i}=k/(n(i-1))。利用公式：
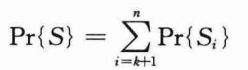
在这里插入图片描述
有：

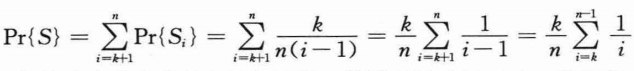
下面利用积分来近似约束这个求和数的上界和下界。根据不等式：

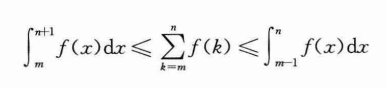
上式中f(k)必须是单调递减函数。则有：

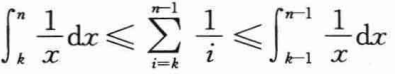
求解这些定积分可以得到：

上式提供了Pr{S}的一个相当紧确的界。因为希望最大化成功的概率，所以关注如何选取k值使Pr{S}的下界最大化。上式中下界表达式比上界表达式更容易最大化。以k为变量对表达式(k/n)(ln n-ln k)求导，得到：
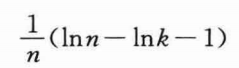
在这里插入图片描述
令上式=0，得到k=n/e，此时Pr{S}的概率下界最大化。因而，如果用k=n/e来实现策略，将以至少1/e的概率成功雇用到最好的应聘者。

2 堆排序

2.1 堆

堆是一种数据结构，使用数组存储堆中的元素，可以将堆看作是一棵完全二叉树。

代表堆的数组A是具有两个属性的对象：

（1）长度length[A]：数组A中元素的数量；

（2）堆的大小heap_size[A]：数组A中存储的堆的元素数量。

有：0≤heap_size[A]≤length[A]。

堆分为两种：

（1）最大堆：除了根之外的每个结点，其双亲结点的关键字均大于等于该结点的关键字，即A[PARENT(i)]≥A[i]。举个栗子：
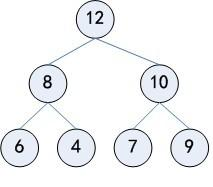
在这里插入图片描述
（2）最小堆：除了根之外的每个结点，其双亲结点的关键字均小于等于该结点的关键字，即A[PARENT(i)]≤A[i]。举个栗子：

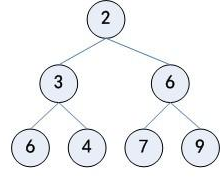
最大堆用于堆排序算法，最小堆用于构造优先队列。

堆的根结点存储在A[1]，即数组A的第一个位置A[0]不存储元素的话，给定堆中某个结点的索引下标i，则有：

（1）结点i的双亲结点的索引下标PARENT(i)=⌊i/2⌋；

（2）结点i的左孩子结点的索引下标LEFT(i)=2i；

（3）结点i的右孩子结点的索引下标RIGHT(i)=2i+1。

把堆看成是一棵完全二叉树后，定义堆中的结点的高度为该结点到叶子结点最长简单路径上边的数目，堆的高度定义为根结点的高度，有n个元素的堆的高度是⌊lgn⌋。只有一个根结点的堆的高度为0。

堆支持的一些操作：

（1）MAX-HEAPIFY：其时间复杂度为O(lgn)，该操作是维护最大堆性质的关键操作。

（2）BUILD-MAX-HEAP：具有线性时间复杂度O(n)，功能是从无序的数组中构造一个最大堆。

（3）HEAPSORT：其时间复杂度为O(n·lgn)，功能是对一个数组进行堆排序，属于就地排序，即任何时候都只需要常数个额外的元素空间去存储临时数据。

（4）MAX-HEAP-INSERT、HEAP-EXTRACT-MAX、HEAP-INCREASE-KEY和HEAP-MAXIMUM：时间复杂度为O(lgn)，功能是利用堆实现一个优先队列。

2.2 维护堆的性质

MAX-HEAPIFY是用于维护最大堆性质的重要过程，输入为数组A和下标i。在调用MAX-HEAPIFY的时候，假定以根结点分别为LEFT(i)和RIGHT(i)的二叉树都是最大堆，但这时A[i]有可能小于其孩子，这样就违背了最大堆的性质。MAX-HEAPIFY通过让A[i]的值在最大堆中“逐级下降”，从而使得以下标i为根结点的子树重新遵循最大堆的性质。

下面是MAX-HEAPIFY的伪代码：

MAX-HEAPIFY(A,i)
    l=LEFT(i)
    r=RIGHT(i)
    if l<=heap_size[A] && A[l]>A[i]
        largest=l
    else
        largest=i
    if r<=heap_size[A] && A[r]>A[largest]
        largest=r
    if largest!=i
        exchange A[i] with A[largest]
        MAX-HEAPIFY(A,largest)

上述伪代码简要地描述了MAX-HEAPIFY的执行过程。在程序的每一步中，从A[i]、A[LEFT(i)]和A[RIGHT(i)]中选出关键字最大的，并将其下标存储在largest中。如果A[i]是最大的，那么以i为根结点的子树已经是最大堆，程序结束。否则，最大元素是i的某个孩子结点，则交换A[i]和A[largest]的值。从而使i及其孩子都满足最大堆的性质。在交换A[i]和A[largest]的值后，下标为largest的结点的值是原来的A[i]，于是以下标为largest的结点为根的子树又有可能会违反最大堆的性质。因此，需要再次对以A[largest]结点为根的子树递归调用MAX-HEAPIFY。

举个栗子，下图是当heap_size[A]=10时，MAX-HEAPIFY(A，2)的执行过程：
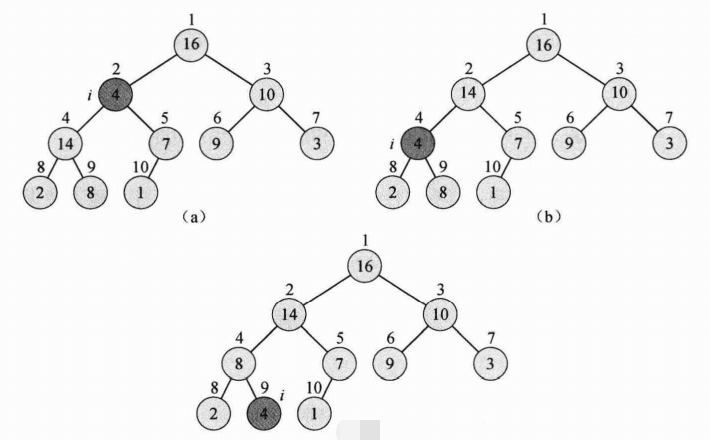
在这里插入图片描述
（1）初始状态，在结点i=2处，A[2]违背了最大堆性质，因为它的值不大于等于它的孩子。

（2）通过交换A[2]和A[4]的值，结点2恢复了最大堆的性质，但又导致结点4违反了最大堆的性质。递归调用MAX-HEAPIFY(A，4)，此时i=4。

（3）通过交换A[4]和A[9]的值，结点4的最大堆性质得到了恢复。再次递归调用MAX-HEAPIFY(A，9)，此时不再有新的数据交换。

对于高度为h的结点来说，MAX-HEAPIFY的时间复杂度是O(h)。由于有n个元素的堆的高度是h=⌊lgn⌋，因此，MAX-HEAPIFY的时间复杂度是O(h)=O(lgn)。

2.3 建堆

可使用自底向上的方法，利用MAX-HEAPIFY把一个大小为n=length[A]的数组A[]转换为最大堆。数组中索引下标为：⌊n/2⌋+1,⌊n/2⌋+2,…,n的元素都是树的叶子结点，每个叶子结点都可以看成只包含一个元素的最大堆。BUILD-MAX-HEAP对树中的非叶子结点都调用一次MAX-HEAPIFY。下面是BUILD-MAX-HEAP的伪代码：

BUILD-MAX-HEAP(A) //使用数组A的元素构建一个最大堆
    heap_size[A]=length[A]
    for i=⌊length[A]⌋ downto 1 //对非叶子结点进行最大堆调整
        MAX-HEAPIFY(A,i)

举个栗子，对于数组A=[4,1,3,2,16,9,10,14,8,7]，下面是使用数组A的元素构建一个最大堆的过程：
在这里插入图片描述
为了证明BUILD-MAX-HEAP的正确性，使用这样的循环不变量——【在伪代码第3-4行中每一次for循环的开始，结点i+1,i+2,…,n都是一个最大堆的根结点】。需要证明的是：① 该循环不变量在第一次循环前为真；② 每次循环迭代都维持不变；③ 当循环结束时，这一不变量可以用于证明正确性。如下：

（1）初始化：在第一次循环迭代之前，i=⌊n/2⌋，而⌊n/2⌋+1,⌊n/2⌋+2,…,n都是叶子结点，因而是只有一个结点的最大堆的根结点。

（2）保持：为了看到每次迭代都维护这个循环不变量，注意到结点i的孩子结点的下标均比i大。所以根据循环不变量，它们都是最大堆的根。这也是调用MAX-HEAPIFY(A，i)使结点i成为一个最大堆的根的先决条件。而且，MAX-HEAPIFY维护了结点i+1,i+2,…,n都是一个最大堆的根结点的性质。在for循环中递减i的值，为下一次循环重新建立了循环不变量。

（3）终止：过程终止时，i=0。根据循环不变量，每个结点1,2,…,n都是一个最大堆的根。而结点1就是所有最大堆中最大的那个堆的根结点。可简单地估算BUILD-MAX-HEAP的运行时间：由于每次调用MAX-HEAPIFY的时间复杂度是O(h)=O(lgn)，BUILD-MAX-HEAP需要O(n)次这样的调用，因此总的时间复杂度是O(n·lgn)。

由于O(n·lgn)并不是渐近紧确的，可以进一步得到一个更紧确的界。由于不同结点运行MAX-HEAPIFY的时间与该结点的高度相关，而且大部分结点的高度都很小。因此，利用这样的性质可以得到一个更紧确的界：包含n个元素的堆的高度为⌊lgn⌋；高度为h的堆最多包含⌈n/2^h+1⌉个结点（我并不清楚为什么是这样）。在一个高度为h的结点上运行MAX-HEAPIFY的代价是O(h)，可将BUILD-MAX-HEAP的总代价表示为：
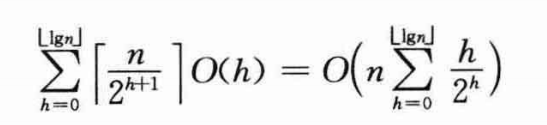
在这里插入图片描述
最后的一个累积和的计算可以用x=1/2带入公式：

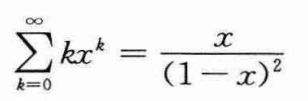
上式中，|x|<1。则有：

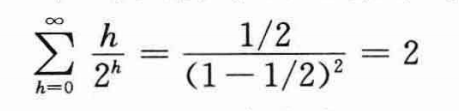
则得到BUILD-MAX-HEAP的时间复杂度：

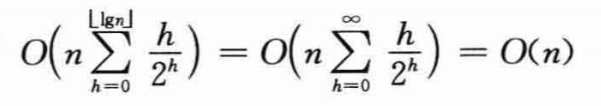
因此可在线性时间内，把一个无序数组构造成为一个最大堆。

除此之外，也可以通过调用BUILD-MIN-HEAP构造一个最小堆。BUILD-MIN-HEAP也可以在线性时间内，把一个无序数组构造成为一个最小堆。下面是MIN-HEAPIFY的伪代码：

MIN-HEAPIFY(A,i)
    l=LEFT(i)
    r=RIGHT(i)
    if l<=heap_size[A] && A[l]<A[i]
        smallest=l
    else
        smallest=i
    if r<=heap_size[A] && A[r]<A[smallest]
        smallest=r
    if smallest!=i
        exchange A[i] with A[smallest]
        MIN-HEAPIFY(A,smallest)

下面是BUILD-MIN-HEAP的伪代码：

BUILD-MIN-HEAP(A) //使用数组A的元素构建一个最小堆
    heap_size[A]=length[A]
    for i=⌊length[A]⌋ downto 1 //对非叶子结点进行最小堆调整
        MIN-HEAPIFY(A,i)

2.4 堆排序算法

初始时，堆排序算法利用BUILD-MAX-HEAP将输入数组A[1…n]建成最大堆，其中n=length[A]。因为数组中的最大元素总在根结点A[1]中，通过把它与A[n]进行互换，就可以将该元素放到正确的位置。这时若从堆中去掉结点n(这一操作可以通过减少heap_size[A]的值来实现)，则在剩余的结点中，原来根的孩子结点仍然是最大堆，而新的根结点可能会违背最大堆的性质。为了维护最大堆的性质，需要做的是调用MAX-HEAPIFY(A，1)，从而在A[1…n-1]上构造一个新的最大堆。堆排序算法会不断重复这一过程，直到堆的大小从n-1降到2。

堆排序算法的伪代码如下：

HEAPSORT(A)
    BUILD-MAX-HEAP(A)
    for i =length[A] downto 2
        exchange A[1] with A[i]
        heap_size[A]--
        MAX-HEAPIFY(A,1)

首先调用BUILD-MAX-HEAP的时间复杂度是O(n)，而算法总共调用了MAX-HEAPIFY有n-1次，其中MAX-HEAPIFY的时间复杂度为O(lgn)，(n-1)·O(lgn)=O(n·lgn)，由此HEAPSORT的时间复杂度取{O(n)，O(n·lgn)}中的O(n·lgn)。

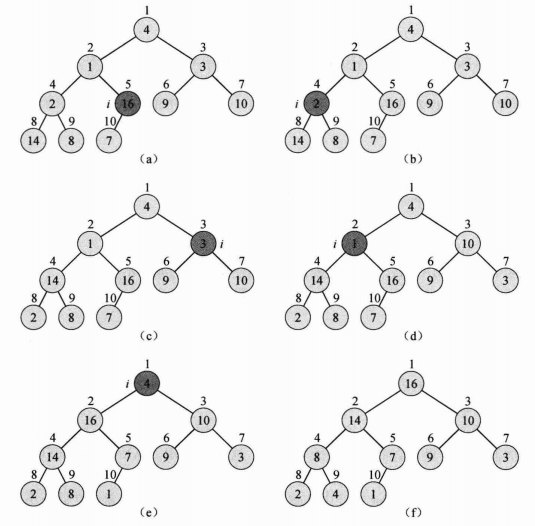
下图给出了一个在HEAPSORT伪代码的第2行建立初始最大堆之后，堆排序操作的一个例子：
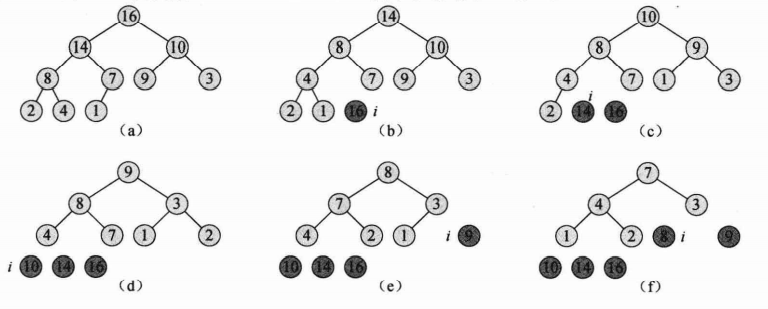
在这里插入图片描述
还没结束，下图为之后的过程：

上面两个图显示了第3-6行for循环第一次迭代开始前最大堆的情况和每一次迭代之后最大堆的情况，其中：(a)执行堆排序算法第2行，是用BUILD-MAX-HEAP构造得到的初始最大堆。(b)~(j)每次执行算法第6行，是调用MAX-HEAPIFY后得到的最大堆，并在图上标记了当前次的i值。其中，仅仅浅色阴影的结点被保留在堆中。(k)是最终的排序结果。

2.5 优先队列

优先队列(priority queue)是一种用来维护由一组元素构成的集合S的数据结构，其中的每一个元素都有一个相关的值，称为关键字(key)。一个最大优先队列支持以下操作：

（1）INSERT(S，x)：把元素x插入集合S中。这一操作等价于S=S∪{x}。

（2）MAXIMUM(S)：返回S中具有最大关键字的元素。

（3）EXTRACT-MAX(S)：去掉并返回S中的具有最大关键字的元素。

（4）INCREASE-KEY(S，x，k)：将元素x的关键字值增加到k，这里假设k的值不小于x的原关键字值。

最大优先队列的应用有很多，其中一个就是在共享计算机系统的作业调度。最大优先队列记录将要执行的各个作业以及它们之间的相对优先级。当一个作业完成或者被中断后，调度器调用EXTRACT-MAX从所有的等待作业中，选出具有最高优先级的作业来执行。在任何时候，调度器可以调用INSERT把一个新作业加入到队列中来。

相应地，最小优先队列支持的操作包括：

（1）INSERT(S，x)：把元素x插入集合S中。这一操作等价于S=S∪{x}。

（2）MINIMUM(S)：返回S中具有最小关键字的元素。

（3）EXTRACT-MIN(S)：去掉并返回S中的具有最小关键字的元素。

（4）DECREASE-KEY(S，x，k)：将元素x的关键字值减少到k，这里假设k的值不大于x的原关键字值。

最小优先队列可以被用于基于事件驱动的模拟器。队列中保存要模拟的事件，每个事件都有一个发生时间作为其关键字。事件必须按照发生的时间顺序进行模拟，因为某一事件的模拟结果可能会触发对其他事件的模拟。在每一步，模拟程序调用EXTRACT-MIN来选择下一个要模拟的事件。当一个新事件产生时，模拟器通过调用INSERT将其插入最小优先级队列中。

优先队列可以用堆来实现。对一个像作业调度或事件驱动模拟器这样的应用程序来说，优先队列的元素对应着应用程序中的对象。通常需要确定哪个对象对应一个给定的优先队列元素，反之亦然。因此，在用堆来实现优先队列时，需要在堆中的每个元素里存储对应对象的句柄(handle)。句柄(如一个指针或一个整型数等)的准确含义依赖于具体的应用程序。同样，在应用程序的对象中，也需要存储一个堆中对应元素的句柄。通常，这一句柄是数组的下标。由于在堆的操作过程中，元素会改变其在数组中的位置，因此，在具体的实现中，在重新确定堆元素位置时，也需要更新相应应用程序对象中的数组下标。因为对应用程序对象的访问细节强烈依赖于应用程序及其实现方式，所以这里不做详细讨论。需要强调的是，这些句柄也需要被正确地维护。

下面讨论如何实现最大优先队列的操作。过程HEAP-MAXIMUM可以在O(1)时间内实现MAXIMUM操作，伪代码如下：

HEAP-MAXIMUM(A)
    return A[1]

HEAP-EXTRACT-MAX实现EXTRACT-MAX操作，伪代码如下：

HEAP-EXTRACT-MAX(A)
    if heap_size[A]<1
        error "heap underflow"
    max=A[1]
    A[1]=A[heap_size[A]]
    heap_size[A]--
    MAX-HEAPIFY(A,1)
    return max

HEAP-EXTRACT-MAX的时间复杂度为O(lgn)。因为除了时间复杂度为O(lgn)的MAX-HEAPIFY以外，它的其他操作都是常数阶O(1)的。

HEAP-INCREASE-KEY能够实现INCREASE-KEY操作，伪代码如下：

HEAP-INCREASE-KEY(A,i,key)
    if key<A[i]
        error "new key is smaller than current key"
    A[i]=key
    while i>1 and A[PARENT(i)]<A[i]
        exchange A[i] with A[PARENT(i)]
        i=PARENT(i)

在优先队列中，希望增加关键字的优先队列元素由对应的数组下标i来标识。这一操作需要首先将元素A[i]的关键字更新为新值。因为增大A[i]的关键字可能会违反最大堆的性质，所以在从当前结点到根结点的路径上，为新增的关键字寻找恰当的插入位置。在HEAP-INCREASE-KEY的操作过程中，当前元素会不断地与其父结点进行比较，如果当前元素的关键字较大，则当前元素与其父结点进行交换。这一过程会不断地重复，直到当前元素的关键字小于其父结点时终止，因为此时已经重新符合了最大堆的性质。

在包含n个元素的堆上，HEAP-INCREASE-KEY的时间复杂度是O(lgn)。这是因为在伪代码第4行做了关键字更新的结点到根结点的路径长度为O(lgn)。

下图显示了HEAP-INCREASE-KEY的一个操作过程：
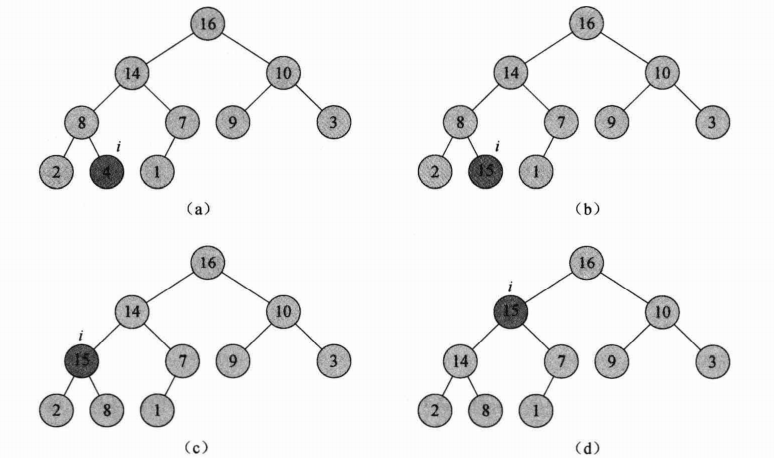
在这里插入图片描述
上图中，(a)表示的最大堆中，下标为i的结点以深色阴影显示。(b)中该结点的关键字增加到15。(c)中经过第5-7行的while循环的一次迭代，该结点与其父结点交换关键字，同时下标i的值上移到其父结点。(d)中经过再一次迭代后得到最大堆。此时，A[PARENT(i)]≥A[i]。现在，最大堆的性质成立，程序终止。

MAX-HEAP-INSERT能够实现INSERT操作。它的输入是要被插入到最大堆A中的新元素的关键字，伪代码如下：

MAX-HEAP-INSERT(A,key)
    heap_size[A]++
    A[heap_size[A]]=-∞
    HEAP-INCREASE-KEY(A,heap_size[A],key)

MAX-HEAP-INSERT首先通过增加一个关键字为-∞的叶子结点来扩展最大堆。然后调用HEAP-INCREASE-KEY为新结点设置对应的关键字，同时保持最大堆的性质。在包含n个元素的堆上，MAX-HEAP-INSERT的运行时间为O(lgn)。

总之，在一个包含n个元素的堆中，所有优先队列的操作都可以在O(lgn)时间内完成。

END

算法导论-上课笔记2:概率分析/随机算法/堆排序/优先队列