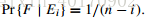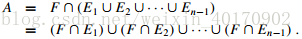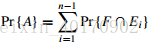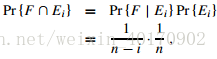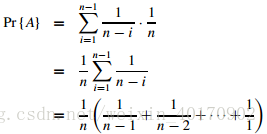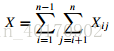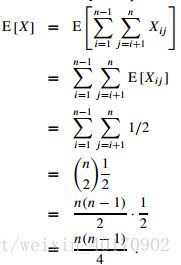练习5.2-2 问题描述:在 HIRE-ASSISTANT中,假设应聘者以随机的顺序出现,正好雇佣两次的概率是多少?
分析:要想正好雇佣两次,首先要考虑三个条件:
1. 候选人i总是被雇佣
2. 最佳候选人,也即候选人n也被雇佣
3. 若最佳候选人是i,则i是唯一的候选人
因此,候选人i的顺序要满足i <= n – 1且所有排序在候选人n之前的i + 1,i + 2,…,n – 1的候选人都被面试了。
令事件表示候选人i被雇佣,则

则事件A即刚好雇佣两次出现的情况是:
事件A出现的概率为:
练习5.2-5 问题描述:假设A[1..n]是由n个不同的数构成的数组。如果i < j且A[i] > A[j],则称(i, j)为逆序对。假设A的元素为1到n的随机排列。利用指示器随机变量来计算A中逆序对的期望数目。
设



根据期望的线性不变性:
因此,逆序对数目的期望值为n(n - 1) / 4
5.3随机算法
随机算法通过排列给定的输入数组来使输入随机化。下面讨论两种随机化方法:
1. 优先级随机化排序PERMUTE-BY-SORTING
思想:为数组A的每个元素A[i]赋一个随机的优先级P[i],然后依据优先级对数组A中的元素进行排序。例如,如果初始数组A=[1,2, 3, 4]且选择随机的优先级P =[36, 3, 97, 19],则将根据指定的优先级得到数列B=[2,4, 1, 3]。这个过程伪代码为:
PERMUTE-BY-SORTING(A)
n ← length(A)
for i ←1 to n
P[i]= RANDOM(1, n^3)
sort A,using P as sort keys
return A
第三行选取1到n^3之间的随机数,为了让P中的所有优先级尽可能是唯一的。此过程的时间复杂度主要体现在第4行中的排序将花费O(nlgn),如果P[i]是第j个最小的优先级,那么A[i]将在输出位置j上。下面来证明这个过程能产生均匀的随机排列,即数字1到n的每一种排列都是等可能被产生。
证明:考虑每个元素A[i]得到第i个最小优先级的特殊排列开始,并证明这个排列发生的概率正好是1/n!。对于i=1,2,…,n,令Xi代表元素代表元素A[i]得到第i个最小优先级的事件,比如A[1]得到的第1个最小优先级。则对所有i,事件Xi发生的概率为
因为Pr{X1}是从n个元素的集合中随机选取优先级是最小的概率,故Pr{X1}=1/n。接下来有Pr{X2|X1}=1/(n-1),由于假定A[1]有最小的优先级,则余下的n-1个元素有相等的成为第2个优先级的可能。一般地对于i=2,3, …, n有:\[\Pr \{ {X_i}|{X_{i - 1}} \cap {X_{i - 2}} \cap \cdot \cdot \cdot \cap {X_1}\} = 1/(n - i + 1)\]这是因为从A[1]到A[i-1]按顺序有前i-1小的优先级,余下的n-(i-1)中,每个具有第i个小优先级的可能性都相同。所以有:\[\Pr \{ {X_1} \cap {X_2} \cap {X_3} \cap ... \cap {X_{n - 1}} \cap {X_n}\} = \left( {\frac{1}{n}} \right)\left( {\frac{1}{{n - 1}}} \right) \cdot \cdot \cdot \left( {\frac{1}{2}} \right)\left( {\frac{1}{1}} \right) = \frac{1}{{n!}}\]
这样就证明了得到同样排列的概率是1/n!。
继续扩展这个证明,使其对任何优先级的排列都起作用。考虑集合{1,2, …, n}的任意一个确定的排列S=[s(1), s(2),…, s(n)]。用Ri代表赋予元素A[i]的优先级排名,其中第j小的元素的优先级名次为j。如果定义Xi为元素A[i]的得到第s(i)优先级的事件,或者Ri=s(i),那么同样的证明仍然适用。因此,如果要计算得到任何特殊排列的概率,这个计算和先前的计算完全相同,所以得到这个排列的概率也是1/n!。
2. 原地排列给定数列的随机排列法
原地随机抽取元素法,即在第i次迭代时,元素A[i]是从元素A[i]到A[n]中随机选取的。第i次迭代之后,A[i]保持不变。程序RANDOMIZE-IN-PLACE在O(n)时间内完成。伪代码如下:
n ←length(A)
for i ←1 to n
swapA[i] ↔ A[RANDOM(i, n)]
下面用循环不变式证明程序RANDOMIZE-IN-PLACE能产生均匀随机排列。给定包含n个元素的一个集合,k排列是包含这n个元素k个元素的序列,共有n!/(n-k)!种可能的k排列。这是由于给定k个位置,从n个元素选元素,第一位置的可能性为n,接着为n-1,…,直到最后一个位置有n-k+1个可能性。所以共有:\[n \cdot (n - 1) \cdot (n - 2) \cdot \cdot \cdot (n - k + 1) = \frac{{n!}}{{(n - k)!}}\]
种可能的k排列。
证明:使用循环不变式:
在第2-3行for循环的第i次迭代之前,对每个可能(i-1)排列,子数列A[1...i-1]包含这个(i-1)排列的概率为(n– i + 1)! / n!。需要证明这个不变式在第一次迭代之前为真,循环的每次迭代能够保持此不变式,并且在循环结束时,次不变式提供一个有用的属性来证明循环结束时的正确性。
初始化:考虑第一次循环迭代之前的情况,i=1。由循环不变式知,对每个可能的0排列,子数组A[1..0]包含这个0排列的概率为(n– i + 1)! / n! = 1。子数列A[1..0]是空的子数组,且0排列也没有任何元素。所以A[1..0]包含所有0排列的概率为1,在第1次循环迭代之前循环不变式成立。
保持:假设刚好在第i次迭代之前,每种可能的(i-1)排列出现在子数组A[1..i-1]中的概率是(n – i + 1)! / n!,要证明在第i次迭代之后,每种可能的i排列出现在子数组A[1..i]的概率是(n– i )! / n!。
考虑一个特殊的i排列,以[x(1),x(2), …, x(i)]来表示其中的元素。这个排列包含一个(i-1)排列[x(1), x(2),…, x(i-1)],接着算法在A[i]中放置的值x(i)的事件用E1表示,它表示前i-1跌代已经在A[1…i-1]构造了此特殊的(i-1)排列。由循环不变式,Pr{E1}=(n– i + 1)! / n!。用E2表示第i次迭代在A[i]中放置值x(i)的事件。E1和E2都发生时,则次特殊的i排列形成。此时概率有:\[\Pr \{ {E_2} \cap {E_1}\} = \Pr \{ {E_2}|{E_1}\} \Pr \{ {E_1}\} \]
概率Pr{E2| E1}等于1/ (n – i + 1),因为算法要从位置A[i..n]的n-i+1个值中随机选取一个值命为x(i)。因此有:\[\Pr \{ {E_2} \cap {E_1}\} = \Pr \{ {E_2}|{E_1}\} \Pr \{ {E_1}\} = \frac{1}{{n - i + 1}}\frac{{(n - i + 1)!}}{{n!}} = \frac{{(n - i)!}}{{n!}}\]
终止:在结束时,i=n+1,的子数组A[1..n]是一个给定n排列的概率为(n- n)! / n! = 1 / n!。
因此,RANDOMIZE-IN-PLACE是可以计算出一个均匀随机排列的。
随机算法通常是解决问题的最简单也是最有效的方法。