前言
本文是结合《算法设计与分析》(骆吉洲)的摘要与上课ppt的笔记。
搜一下
面试+算法岗
第一章:绪论
1.1 算法在计算机科学体系中的地位
1.1.1 计算机理论模型和计算问题的分类
计算:
- 是能够在某种计算装置上机械的执行的一个操作序列
- 计算必须在特定的计算装置上完成
计算模型——图灵机
| 组成 | 作用 |
|---|---|
| 有限状态控制器 | 记住有限种状态 |
| 读写头 | 读写存储带上的符号 |
| 单项无线的存储带 | 由存储单元构成,每个单元记录一个符号,每个符号允许擦除和写入,其所占用存储单元的数量n称为问题的输入规模 |
| 有限条计算规则 | 规定当前状态q下存储带上读到当前符号a时应该转入状态q‘,同时在存储带的当前位置写下符号b,读写头向右(或向左)移动一个单元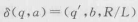 |
图灵机求解计算问题时:
- 计算过程执行的计算规则的个数表示成输入规模n的f(n),称为图灵机的时间复杂度;
- 计算过程中使用的不同存储单元的个数表示成输入规模n的函数g(n),称为该图灵机的空间复杂度。
1.1.2 利用计算机求解问题
通用图灵机的存在性命题:即存在一个通用图灵机M,它能够模拟任何图灵机执行计算。
设计图灵机的三个步骤:
①确定计算过程需要的符号集
②确定图灵机的状态集
③确定图灵机的有穷计算规则
1.1.3 计算机科学的知识体系
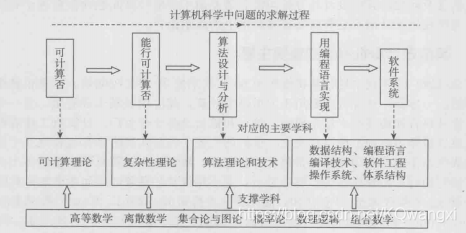
- 能够求解一个问题的图灵机称为该问题对应的算法。
- 可计算问题:存在算法的计算问题;因为每个图灵机均可以被编码成二进制形式(机器代码),进而可以看成一个自然数,故所有可计算问题构成的集合可以看成自然数集,是可数的。
- 计算问题若可计算,还需要通过是否存在时间复杂度f(n)是n的多项式来判定它是否是能行可计算
1.1.4 算法是计算机科学的重要主题
1.1.5 算法设计与分析的意义
- 算法是计算机的灵魂:计算机本身是通用算法的物理实现
- 算法是计算机各领域的核心
1.2 算法的概念
算法是一组有穷的规则,它规定了解决某一特定类型问题的一系列有效的计算。
有效性有三层含义:
①算法必须是有目的的计算,算法能根据输入给出相应的输出
②算法必须在优先计算步骤内停止
③算法执行的每个计算步骤必须是在输入数据和之前的计算步骤得到的计算结果的基础上采取的明确的可机械完成的计算步骤
算法的特征:
①有穷性——算法会在合理的有限步骤之后终止
②确定性——一个算法的每个步骤都必须精确定义
③能行性——指算法中有待实现的运算都是基本的运算
④输入——0个或多个输入
⑤输出——1个或多个输出
计算问题的本质是刻画输入和输出之间的关系。
书写算法步骤:
①给出算法名称
②描述算法求解的计算问题
③依次列出算法的操作步骤,每个步骤前用阿拉伯数字编号
1.3 算法分析
1.3.1 算法正确性分析
算法的正确性分析旨在证明算法在问题的所有输入上能够产生正确的输出。
以循环不变量方法为例
- (循环不变量)首先定义算法的循环体所操作的数据上的一个关键性质
- (初始)证明该性质在循环体首次被执行之前是成立的
- (循环不变)证明循环体每次执行之后该性质仍然成立
- (终止)证明算法结束时该关键性质保证了算法的正确性。
1.3.2 算法复杂度分析
算法复杂度分析是对算法的量化分析,对一个算法需要多少计算时间和存储空间的统计(时间、基本操作的个数、空间、I/O次数、能源)
运行时间的度量:
- 使用时间标准度量单位
- 统计算法中基本操作(通常是算法最内层循环中最费时的操作)的执行次数
对数级的算法大规模数据上的表现非常好;指数级的算法只能解决规模非常小的问题
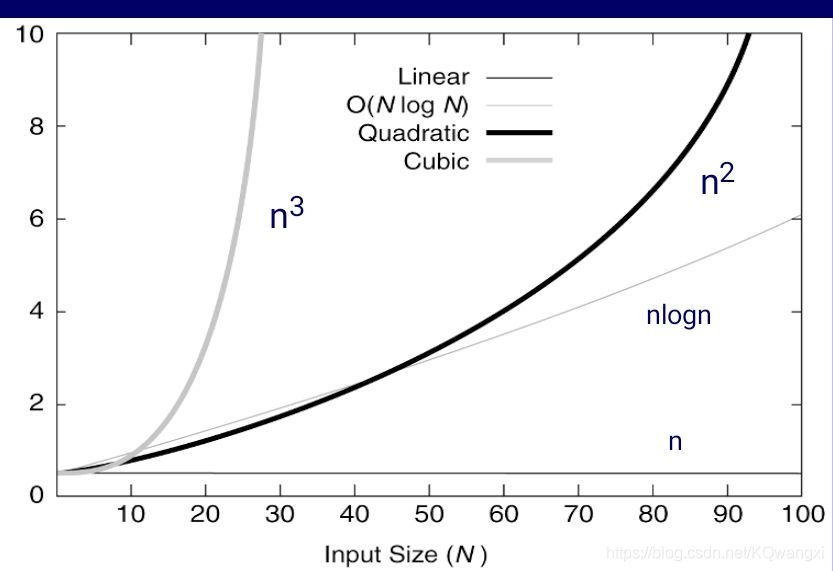
计算时间的渐进表示
n: 问题的规模
f(n): 算法的运行时间(度量单位为基本操作的运行次数)
g(n): 形式简单的函数
计算机科学家使用如下三种符号表示g(n)对f(n)的渐近: - O
- Ω(读omega)
- Θ(读theta)

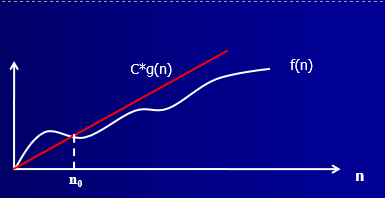
O
如果存在两个正常数c和n0,对于所有的n≥ n0,有| f(n) |≤ c| g(n) |,则记做f(n) =O(g(n) ),称g(n)是计算时间f(n)的一个渐近上限;O(g(n))指的是一个集合
定理:
-
若A(n)=amnm+……+a1n+a0是一个m次多项式,则A(n)=O(nm)
-
f(n) = O(g(n) ),说明:
- 1)说明g(n)是f(n)的渐近上限
- 2)说明f(n)的时间复杂度不高于g(n)
- 3)即便是最坏情况下, f(n)的时间复杂度也不会高于g(n)

Ω
如果存在两个正常数c和n0,对于所有的n≥n0,有| f(n) | ≥ c | g(n) |,则记做 f(n) = Ω(g(n) ),称g(n)为f(n)的渐近下限。

f(n) =(g(n) ),说明什么?
- 说明g(n)是f(n)的渐近下限
- 说明f(n)的时间复杂度不低于g(n)
- 即便是最好情况下, f(n)的时间复杂度也不会低于g(n)
Θ
(读theta)
如果存在正常数c1, c2和n0,对于所有的
n≥n0,有c1 | g(n) |≤ | f(n) | ≤ c2 | g(n) | ,则记做f(n) =Θ(g(n) ) .称g(n)为f(n)的渐进紧确界。
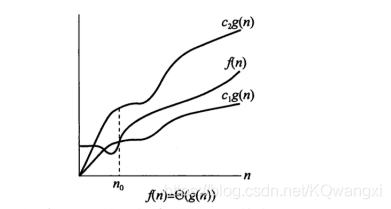
若f(n) =Θ(g(n) ) ,说明
f(n)和g(n)时间复杂度相同,或者说二者是“同阶”的