算法竞赛进阶指南---一个简单的整数问题2 （分块）

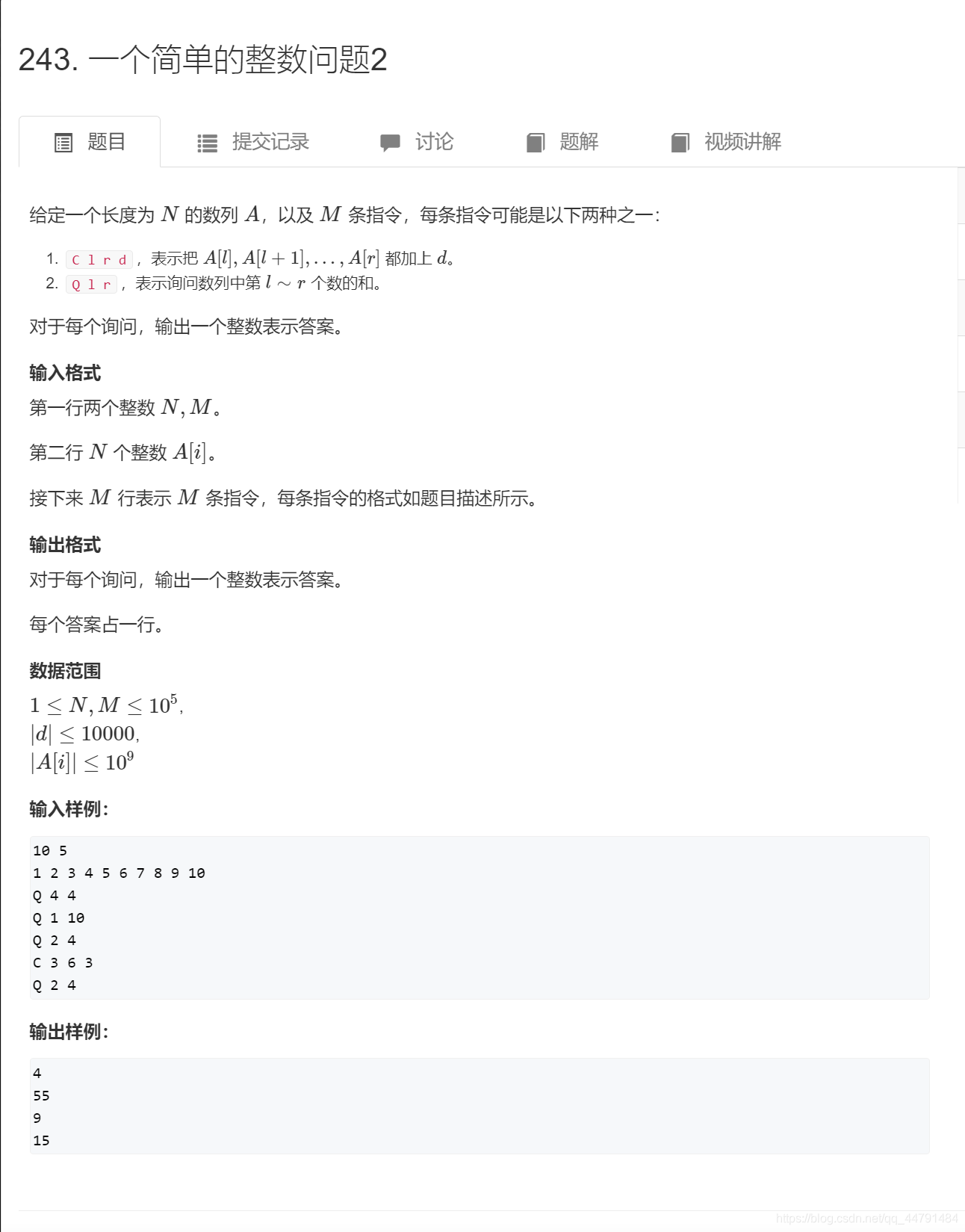
题面

题解

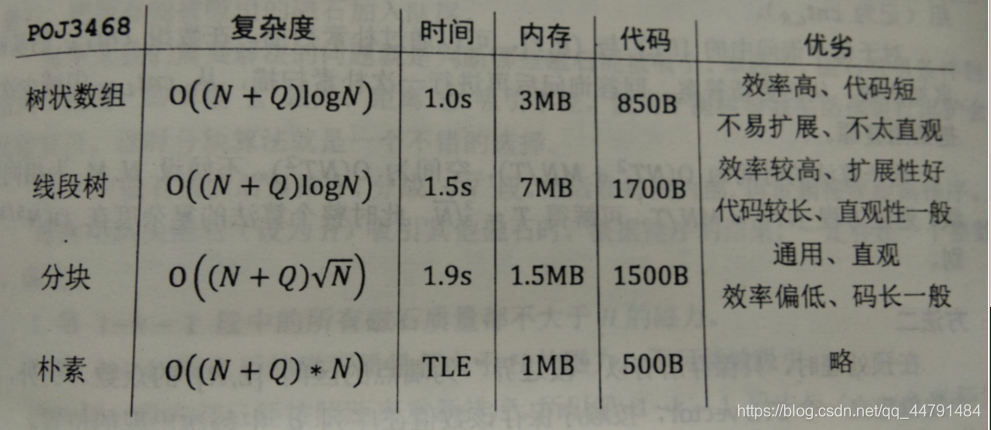
分块的基本思想：通过适当的划分，预处理一部分信息并保存下来，用空间换取时间，以达到时空平衡。通过表我们也有看出，分块的效率比不上树状数组和线段树，但是它更通用，容易实现。

回忆：解决这个问题，有区间修改和区间查询，我们最直接的想法就是用线段树来做，，然后经过差分公式的推导，发现树状数组也可以做，附上做法 。那么接下来看分块的做法

对于序列A，我们将其分成若干个长度不超过 t = sqrt(n) 的段，其中左端点为 (i-1) * t +1,右端点为min( i * t ,N )

我们还需要定义两个数组 sum[] 和add[], sum[i] 表示分段之后第 i 段的和 ；add[i] 表示第 i 段的 ‘增量标记’ ,（就是给这段的每一个数都加上一个d，我们这里是做个标记，等到计算的时候再加上这个标记）

对于操作‘C l r d’

1. 若 l 和 r 在同一段内，我们直接把A[l],A[l+1],…,A[r] 都加上一个d，同时令 sum[i]+=(r-l+1) *d
2. 否则设 l 在 p 段， r 在 q 段

1. 对于 [p+1,q-1] 段，这些数都要加上一个d ，那么我们可以打一个标记，就是之前说到的 add[i]+=d; 表示第 i 段的每个数都加上一个d
2. 对于开头结尾不足一整段的两部分，按照第一种情况更新即可 sum[p]+=(R[p]-l+1)*d 和 给区间 [l ,R[p] ] 中的每一个数都加上一个d ，右边也是相同的道理

对于操作‘ Q l r’

1. 若 l 与 r 同时处于第 i 段内，则 （A[l] + A[l+1] + … +A[r]）+ add[i] * (r-l+1) 就是答案
2. 否则，设 l 处于第 p 段，r 处于第 q 段，初始化 res = 0

1. 对于 [p+1,q-1] 段， res+= sum[i] + add[i] * ( R[i] - L[i] + 1 )
2. 对于开头，结尾不足一整段的两部分,按照与第一种情况相同的计算方式即可

这种分块算法对于整段的修改用标记add记录下来，对于不足整段的修改采用朴素算法。因为段数和段长都是O(sqrt(N))，所以整个算法的时间复杂度为O((N+Q)* sqrt(N)) 大部分常见的分块思想都可以用“ 大段维护，局部朴素”

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>

using namespace std;
typedef long long ll;
const int N = 1e5 + 10;

ll a[N];   //输入数组
ll sum[N];  //区间和(分段之后)
ll add[N];  //增量标记
ll L[N], R[N];  //每段左右下标
ll pos[N];   //每个位置属于哪一段
ll n, m, t;

//给l-r加上d
void change(ll l, ll r, ll d) {
    
    
    ll p = pos[l], q = pos[r];
    if (p == q) {
    
      //在一段区间上,朴素处理
        for (int i = l; i <= r; i++) a[i] += d;
        sum[p] += (r - l + 1) * d;
    } else {
    
      //在不同的区间
        //区间中的所有数都要加上d,给每个区间做个标记
        for (int i = p + 1; i <= q - 1; i++) add[i] += d;
        //左边
        for (int i = l; i <= R[p]; i++) a[i] += d;
        sum[p] += (R[p] - l + 1) * d;
        //右边
        for (int i = L[q]; i <= r; i++) a[i] += d;
        sum[q] += (r - L[q] + 1) * d;
    }
}

//询问区间和
ll ask(ll l, ll r) {
    
    
    int p = pos[l], q = pos[r];
    ll res = 0;
    if (p == q) {
    
    
        for (int i = l; i <= r; i++) res += a[i];
        res += add[p] * (r - l + 1);
    } else {
    
    
        for (int i = p + 1; i <= q - 1; i++)
            res += sum[i] + add[i] * (R[i] - L[i] + 1);
        for (int i = l; i <= R[p]; i++) res += a[i];
        res += add[p] * (R[p] - l + 1);
        for (int i = L[q]; i <= r; i++) res += a[i];
        res += add[q] * (r - L[q] + 1);
    }
    return res;
}

int main() {
    
    

    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];

    t = sqrt(n);  //分块后每段的长度
    for (int i = 1; i <= t; i++) {
    
    
        L[i] = (i - 1) * t + 1;
        R[i] = i * t;
    }

    if (R[t] < n) {
    
      //最后一段
        t++;
        L[t] = R[t - 1] + 1;
        R[t] = n;
    }

    //预处理
    for (int i = 1; i <= t; i++) {
    
       //所有区间
        for (int j = L[i]; j <= R[i]; j++) {
    
       //每段的左右端点
            pos[j] = i;  //每个位置属于哪一段
            sum[i] += a[j];  //区间的和
        }
    }

    while (m--) {
    
    
        string op;
        ll l, r, d;
        cin >> op >> l >> r;
        if (op == "C") {
    
    
            cin >> d;
            change(l, r, d);
        } else {
    
    
            cout << ask(l, r) << endl;
        }
    }

    return 0;
}