关注公众号,查看更多区块链科研内容:
一、The One Time Pad (OTP) - 一次性密码本
对称密码定义:
a cipher defined over ( K , M , C ) (K, M, C) (K,M,C) is a pair of “efficient” algs ( E , D ) (E, D) (E,D) where E : K ∗ M → C , D : K ∗ C → M E: K * M \rightarrow C, D: K * C \rightarrow M E:K∗M→C,D:K∗C→M s.t.
∀ m ∈ M , k ∈ K : D ( k , E ( k , m ) ) = m \forall m \in M , k \in K: D(k, E(k, m)) = m ∀m∈M,k∈K:D(k,E(k,m))=m
K是密钥空间,M是明文空间,C是密文空间
E一般称为加密算法,D一般称为解密算法
一次密码本:

OTP的主要缺点就是密钥与明文等长
OTP是安全的嘛?先看看什么是安全密码的定义:
香农给出了完全安全的定义:

对于完美/完全安全来说,任何的唯密文攻击无效
证明OTP是一个完全安全的密码:

对于OTP来说分子的常量就是1,因为对于一个明文加密为密文有且仅有一个密钥与之对应,所以OTP是完全安全的

但是前面说过OTP的密文需要和明文一样长,这就在实际的使用中出现了难度,第二节就会引入实际中的解决办法
如果想让实现这样的安全性,加密10G的明文就需要10G的密钥,这样是难以实现的

二、Steam Ciphers - 流密码
2.1 Pseudorandom Generators - 伪随机生成器
完全安全(Prefect Secrecy)意味着能够防御唯密文攻击(CT only attack)
但是要求: 秘钥长度 >= 明文长度
为了让流密码实现完全安全, 但是不可能这么长的随机密钥, 所以就产生了 => 伪随机生成器PRG
make OTP practical 让OTP实用化
PRG的定义:
一个函数, $G: {0,1}^s \rightarrow {0,1}^n, n >> s $
从种子空间(随机空间)通过函数G映射到更大的空间, n远大于s, 其中G是一个确定性函数
唯一有随机性的是种子空间, 输出结果是“看起来随机”
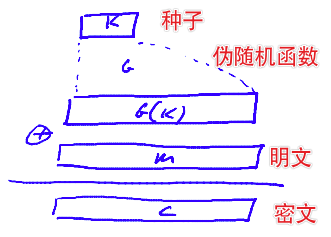
显然, 这样的伪随机数不是完全安全的, 但是安全可以依赖于一种特殊的PRG
PRG的预测性讨论
特殊PRG的要求: 不可预测性
可预测性
可预测性指的是:
$\exists i: G(k)|{1,…,i} \rightarrow G(k)|{i+1,…,n} $
可预测性: 根据生成的G(k)的前缀可以预测剩下的内容(哪怕仅仅只能预测一位)
可预测性定义:
∃ ′ e f f ′ a l g A a n d ∃ 0 ≦ i ≦ n − 1 s . t . Pr k ← R K [ A ( G ( k ) ∣ 1 , … , i = G ( k ) ∣ i + 1 ] > 1 / 2 + ε \exist \ 'eff' \ alg \ A \ and \ \exist_ {0\leqq i\leqq {n-1}} s.t. \ \Pr\limits_{k \xleftarrow{R}K}[A(G(k)|_{1,…,i} = G(k)|_{i+1}] > 1/2 + \varepsilon ∃ ′eff′ alg A and ∃0≦i≦n−1s.t. kRKPr[A(G(k)∣1,…,i=G(k)∣i+1]>1/2+ε
解释: 存在可预测函数A能够实现, 从G(k)的0~i位预测第i+1位的概率大于二分之一 + 不可忽略的量(2.2会详细解释),那么就称G(k)是可预测的
一旦G(k)是可预测的,那么就一定是不安全的!
不可预测性
定义: 对于G(k)所有的位置i没有一个有效函数A以不可容忍的概率预测出i+1的位置的值
理解了可预测性,不可预测其实就是和其相反
例子
线性同余法(lin cong)的方法基本都是可预测性的伪随机生成器, 所以都是不安全的

Kerberos V4 采用了以上的方法所以被攻破了
2.2 Negligible vs non-negligible - 可忽略与不可忽略
本节针对于上方的不可忽略的量: ε \varepsilon ε
对于是否可以忽略,不同的密码学角度有不同的看法,分别是:实用主义和理论主义
-
实用主义认为该量是一个阈值
- 如果 ε ≥ 1 / 2 30 \varepsilon \ge 1/2^{30} ε≥1/230则不可忽略
- 如果小于 ε ≤ 1 / 2 80 \varepsilon \le 1/2^{80} ε≤1/280则可以忽略
-
理论主义认为其是一个由安全参数函数生成的变量
λ d \lambda ^d λd就是一个多项式函数的下界值
-
如果 ε \varepsilon ε 经常大于 1 / λ d 1/\lambda^d 1/λd的值,那么可以说其是不可忽略的
-
相反,如果所有函数值都小于多项式的值那么其就是可以忽略的
-

一些例子:

总结: 一般小于指数级小的认为可以忽略,而大于多项式级小的认为不能忽略
2.3 Attacks on OTP and stream ciphers - 针对OTP和流密码的攻击
OTP使用真随机序列,流密码使用伪随机序列, 他们的密钥都与明文一样长
流密码无法实现香农定义的完美安全,但是他的安全性在于PRG函数的不可预测性, 本节将会对流密码的安全性做一个更完整的定义
1. 两次密码本攻击
之所以叫OTP一次性密码本,是因为该加密方式只能加密单次信息. 如果为不同的明文加密就不安全了:

=> 流密码的密钥永远不要使用两次
802.11b WEP的例子:
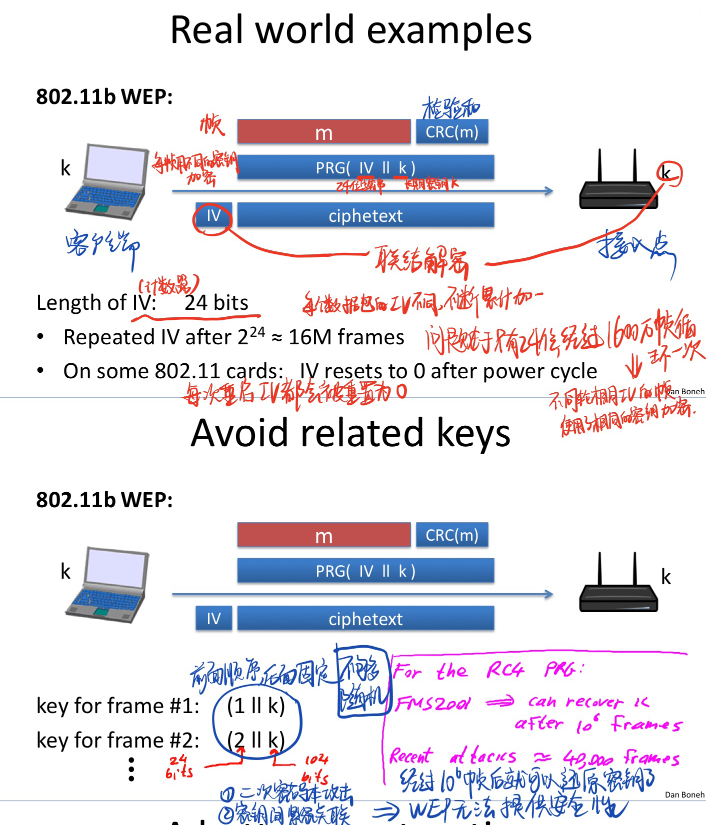
好的做法:
使用伪随机数生成器生成一段随机数,分割成小段随机数给每一个帧加密:
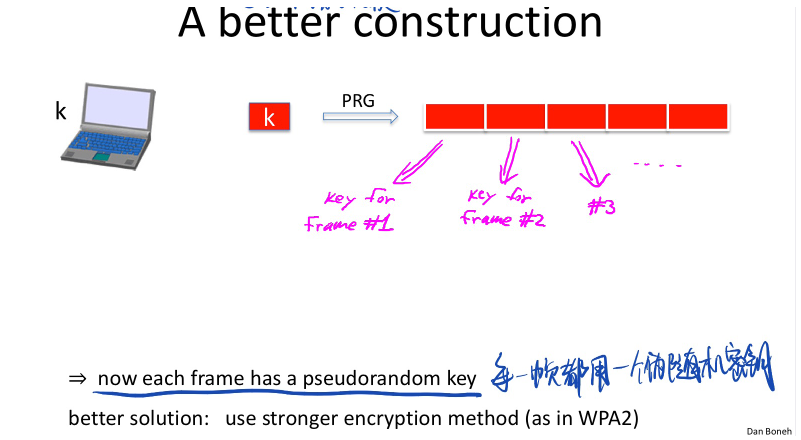
流密码是对位加密的,单个位的改变在密文上很容易看出来,所以对于硬盘加密不适合使用流密码加密:
本质上来说,下面的例子中未修改的部分还是出现了二次加密违背了一次一密
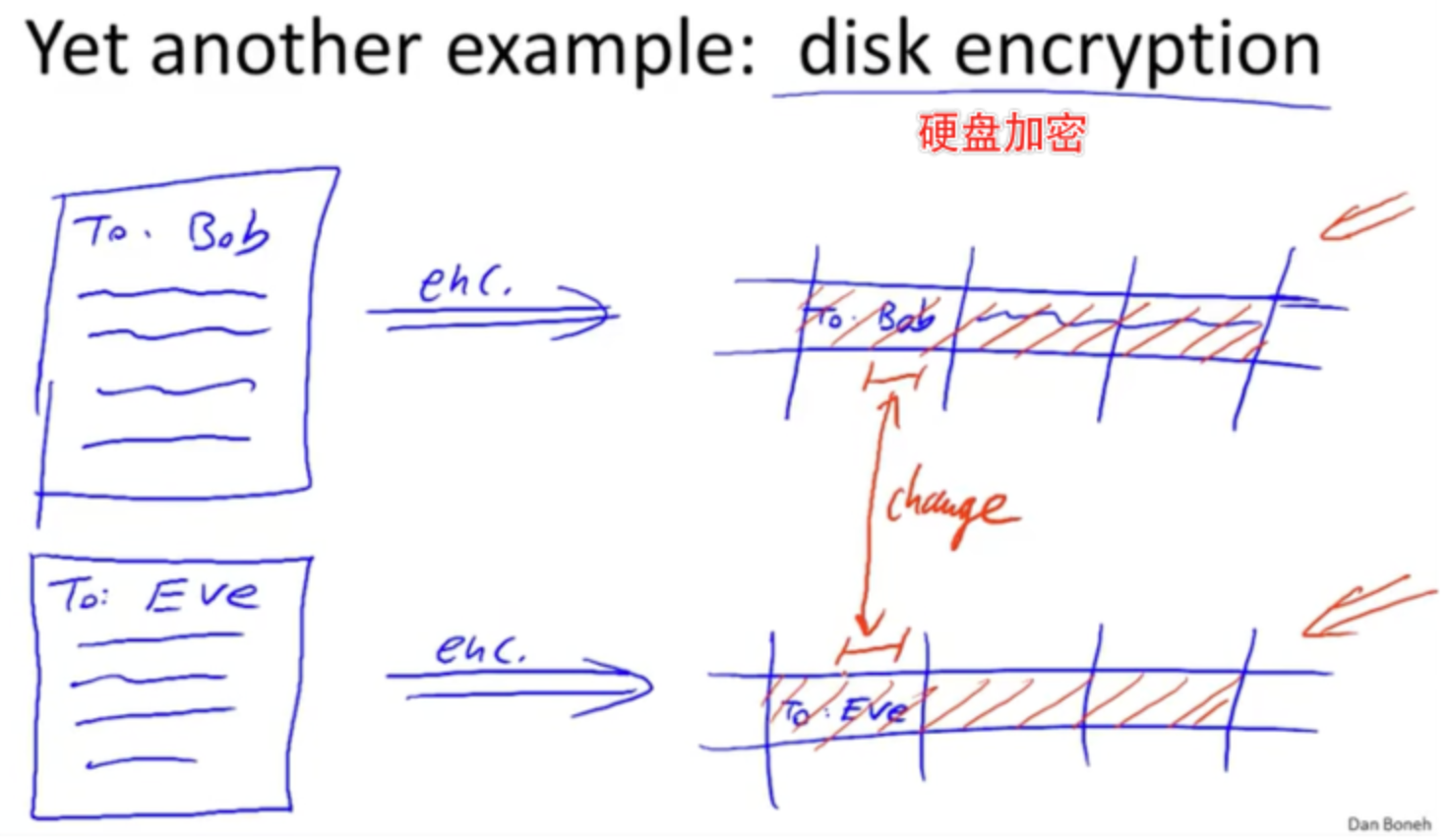
两次密码本攻击总结:
- 网络流量每次会话都要商讨新的密钥对
- 硬盘加密不要使用流密钥加密
2. 完整性保护
OTP或者是流密码只提供私密性保护,都不提供完整性的保护, OTP is malleable
也即:通过修改密文让其还原成明文变得困难
攻击过程举例:
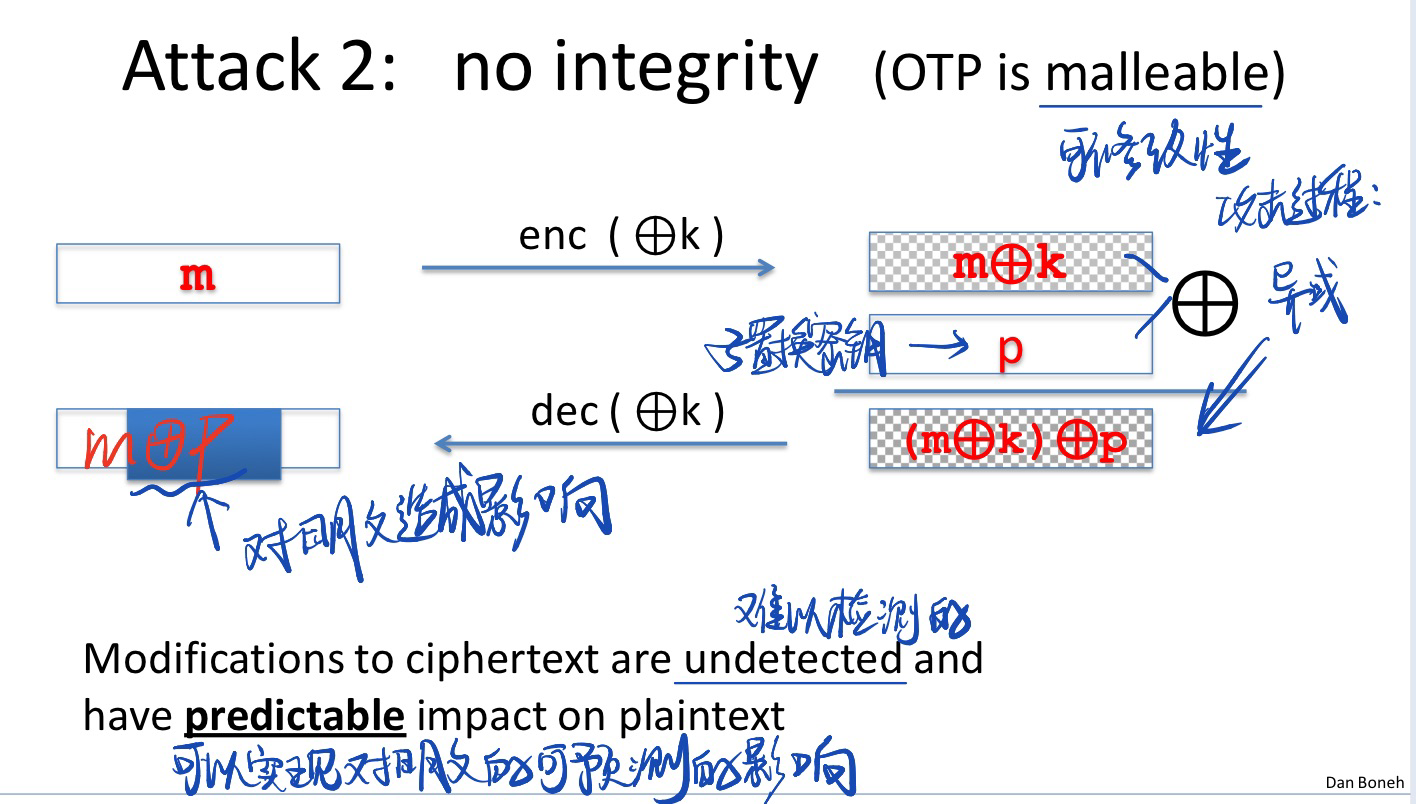
在实际邮件发送过程中的攻击举例:
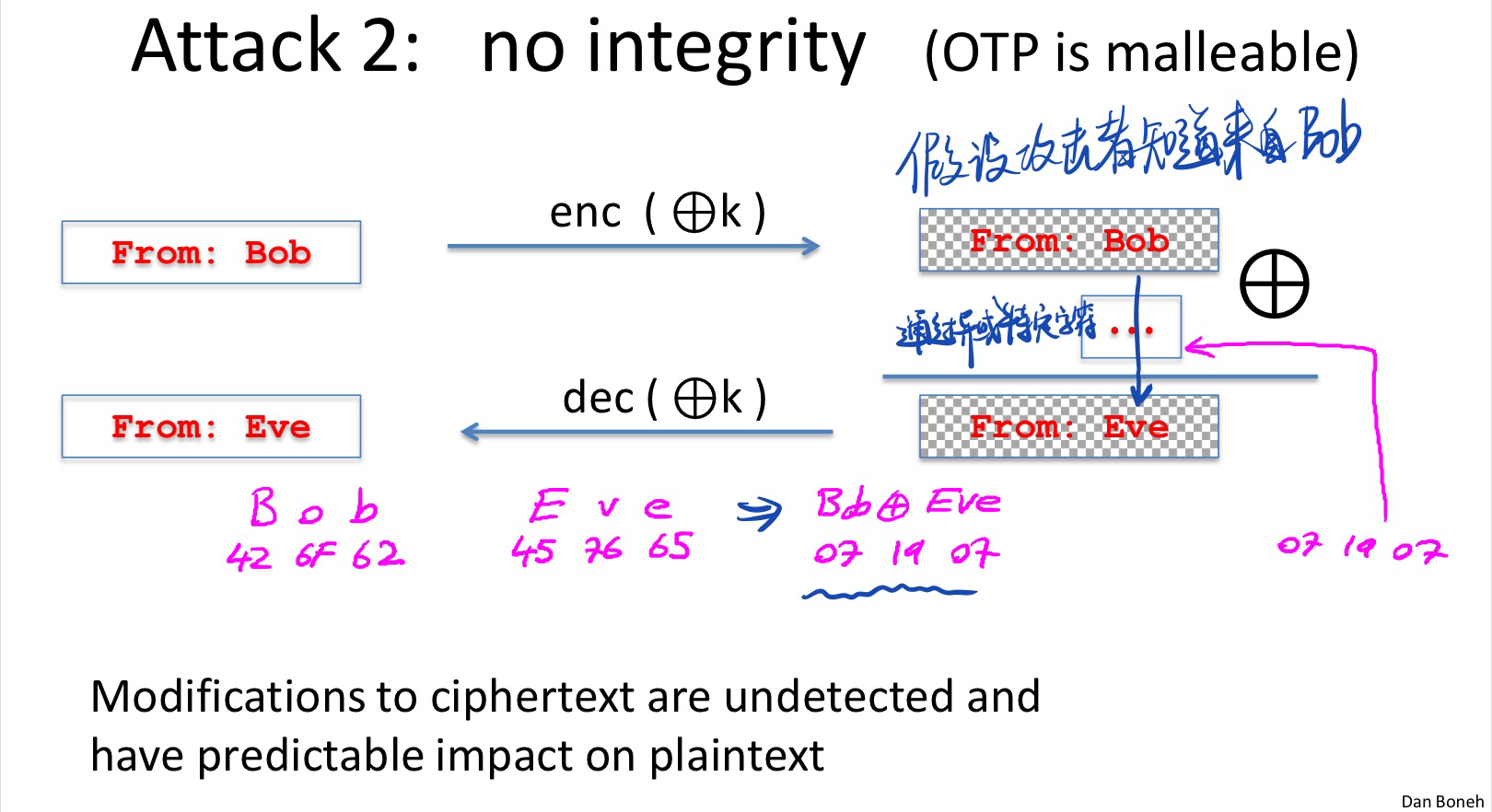
总结:一次性密码本本身对于完整性没有任何保护,所以单纯的使用其是不安全的
2.4 流密码实际应用
1. 流密码生成器RC4(软件)
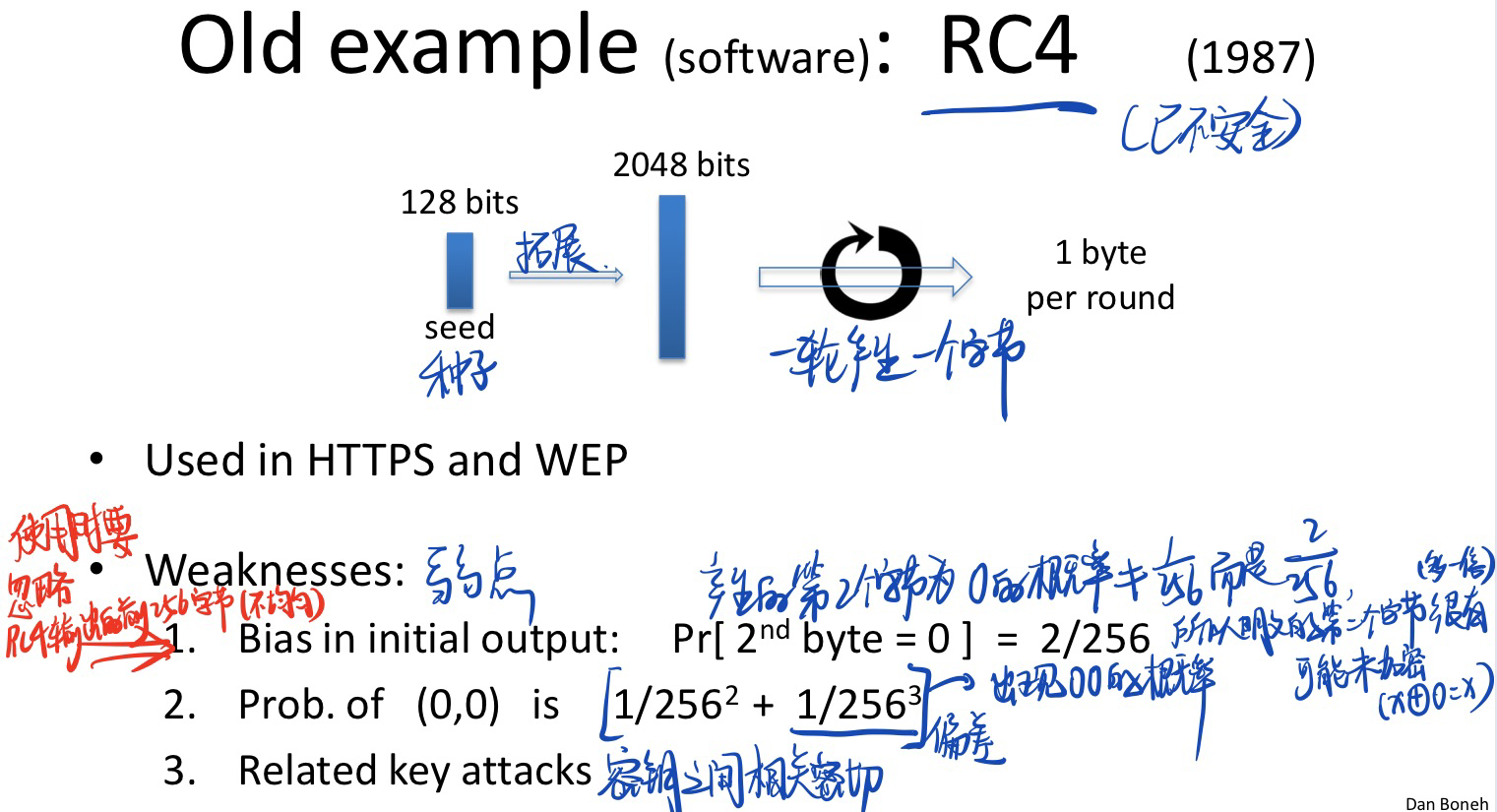
总结: RC4生成器的随机密钥生成随机性不均匀,所以已不建议使用
2. 混淆系统CSS (硬件)
加密DVD电影使用的CSS原理:
寄存器不断像右移位,几个“出头”读取数据异或放到左侧
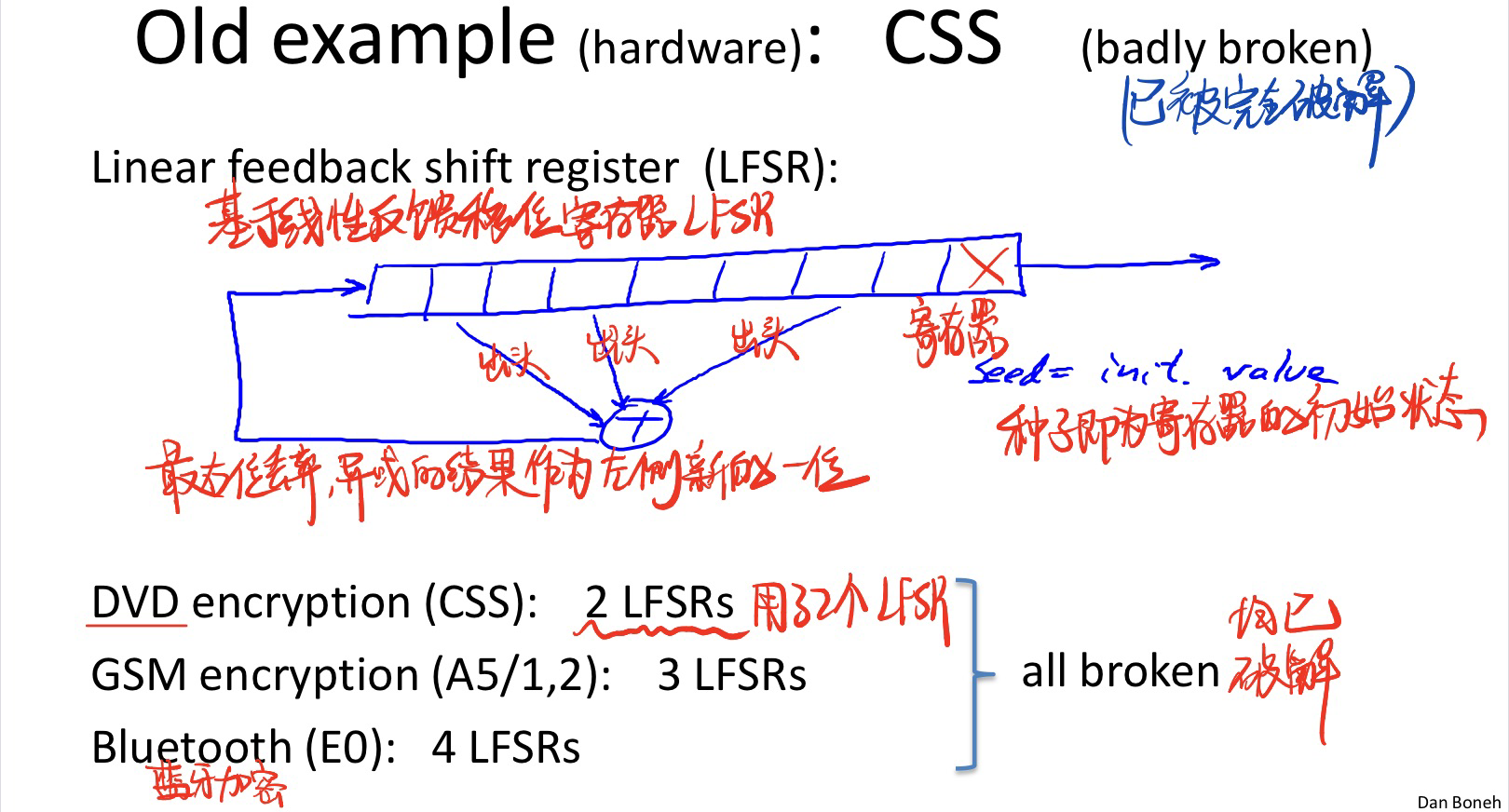
(注:最右位输出,每次输出一位)
CSS的加密过程以及破解的步骤:
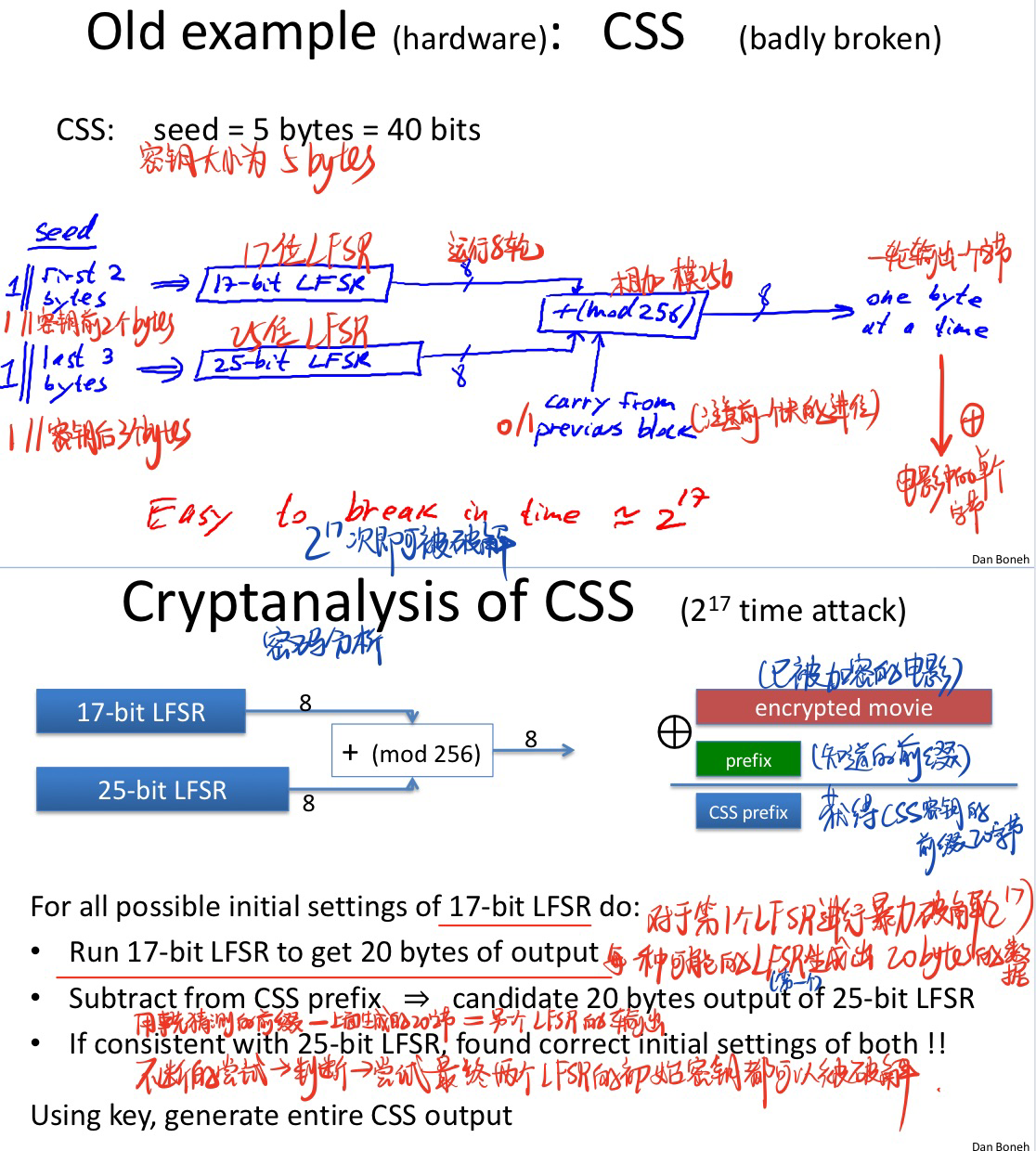
可以被破解的原因:两个LFSR关联性太过简单(直接相加),17-bit LFSR位数太少容易被暴力破解
3. 现代流密码-eStream
其基本构成如下,在一般的PRG基础上增加了随机数Nonce

eStream的一个特例是Salsa,其生成原理如下:
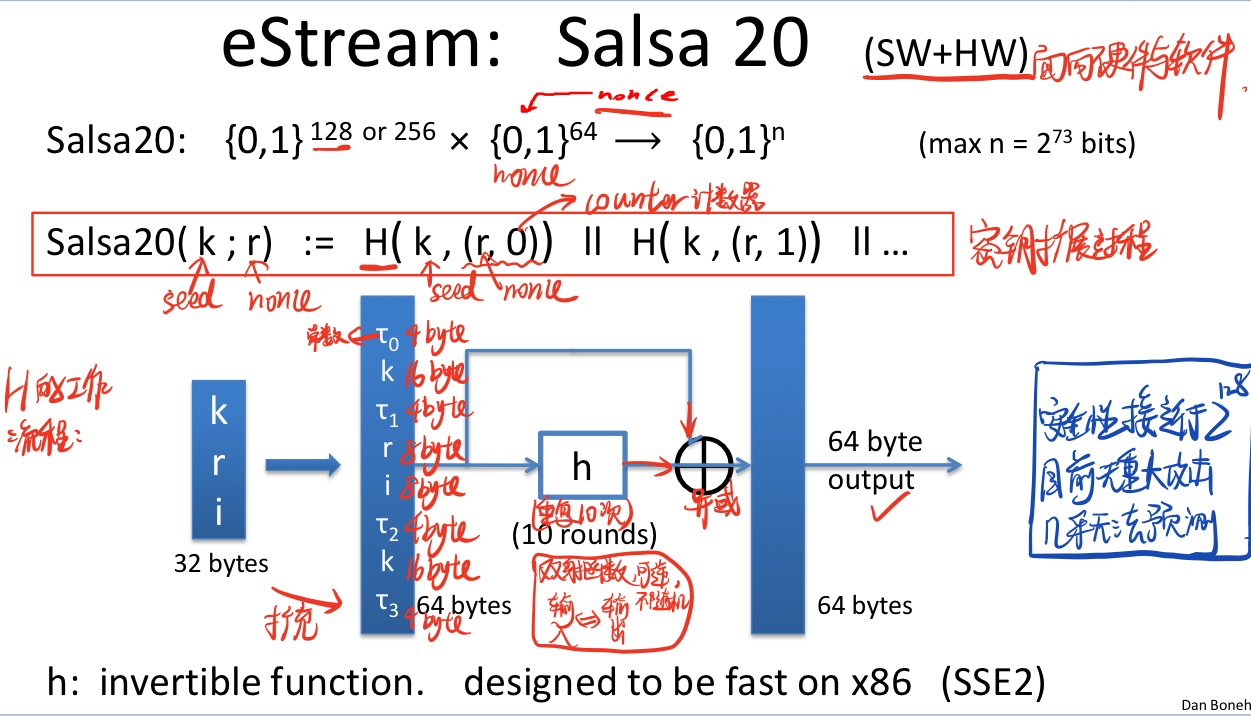
4. 性能对比
 5. 提高随机性
5. 提高随机性
实际中伪随机数生成器提高随机性的方法:
- 持续注入熵增
- 熵增来源:
- Hardware RNG: 从硬件随机生成器中获取随机数
- 时序:Hardware interrupts(硬件中断)(键盘、鼠标)
2.5 PRG Security Defs - PRG安全定义
目标
目标:即使在PRG种子空间很小的情况下,攻击者也无法区分其输出与均匀随机分布 { 0 , 1 } n \{0,1\}^n { 0,1}n(也就是真随机)的区别

统计测试
可以对伪随机数生成器生成的随机数进行统计学上的随机测试,测试其是否具有随机性,老师举了一下三个例子:

统计测试函数A的优势
优势的定义:判定一个统计测试函数对于伪随机生成器和真随机的区分能力,也即评估这个统计测试函数的优劣
其计算公式定义如下:

一个计算优势的例子:

=> A以1/6优势破解了发生器G
PRG的密码学安全性定义
了解了统计测试,下面优雅的PRGs的安全定义就可以给出了:

安全定理的事实
由安全定理可以推出一些简单的事实:
一个PRG可预测 => 此PRG不安全

姚期智教授 证明了其逆命题也成立:
一个PRG不可预测 => 此PRG是安全的

安全定理的推广
证明同一个均匀分布下的两个不同独立分布在计算上的不可区分性:

一个PRG安全的公式表示:
{ k ← R K : G ( k ) ≈ p u n i f o r m ( { 0 , 1 } n ) } \{k \xleftarrow{R}K: G(k) \thickapprox_p uniform(\{0,1\}^n) \} { kRK:G(k)≈puniform({ 0,1}n)}
意义:G(k)与均匀分布 { 0 , 1 } n \{0,1\}^n { 0,1}n在多项式的时间内不可区分
2.6 Semantic security - 语义安全
本节主要的目标是将上一节的安全PRG推广到安全流密码
2.6.1 安全密码定义的演变
从攻击者仅知晓密文的角度来讨论安全密码的定义:
(密码学的安全要看讨论的角度)

最终香农总结出了他饿看法:
CT攻击者学习不到/预测不到任何相关明文PT的信息
会看香农的完美密码定义:

实际安全密码对完全安全密码定义弱化的内容:
- 严格不可区分 => 在多项式的时间内计算上不可区分
- 所有的 ( m 0 , m 1 ) (m_0, m_1) (m0,m1) => 攻击者所知道的明文 ( m 0 , m 1 ) (m_0, m_1) (m0,m1)
2.6.3 语义安全定义(one-time key)
对于两个实验,如果攻击者的优势很小可忽略,那么此对称加密算法是难以被区分的

2.6.4 示例
1.不安全对称加密的可区分例子:攻击者可以从密文中推断出明文的最低位
只要有明文的任何信息被学习到都是不安全的

2. OTP语义安全的证明
由XOR的性质, k ⊕ m 0 k \oplus m_0 k⊕m0和 k ⊕ m 1 k \oplus m_1 k⊕m1是完全独立同分布的,所以OTP是严格上的语义安全:
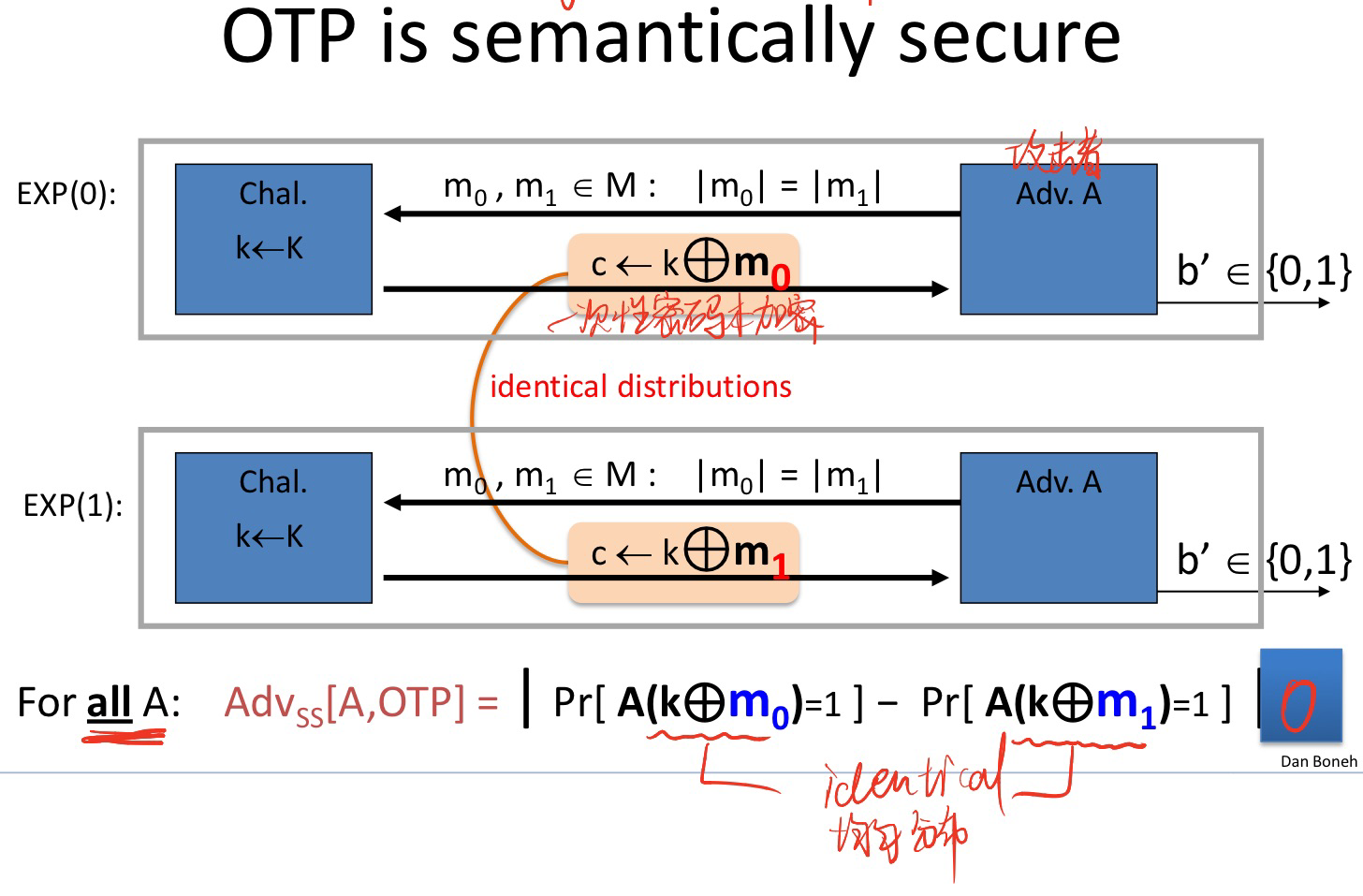
2.7 流密码是语义安全密码
直观上的证明思路:
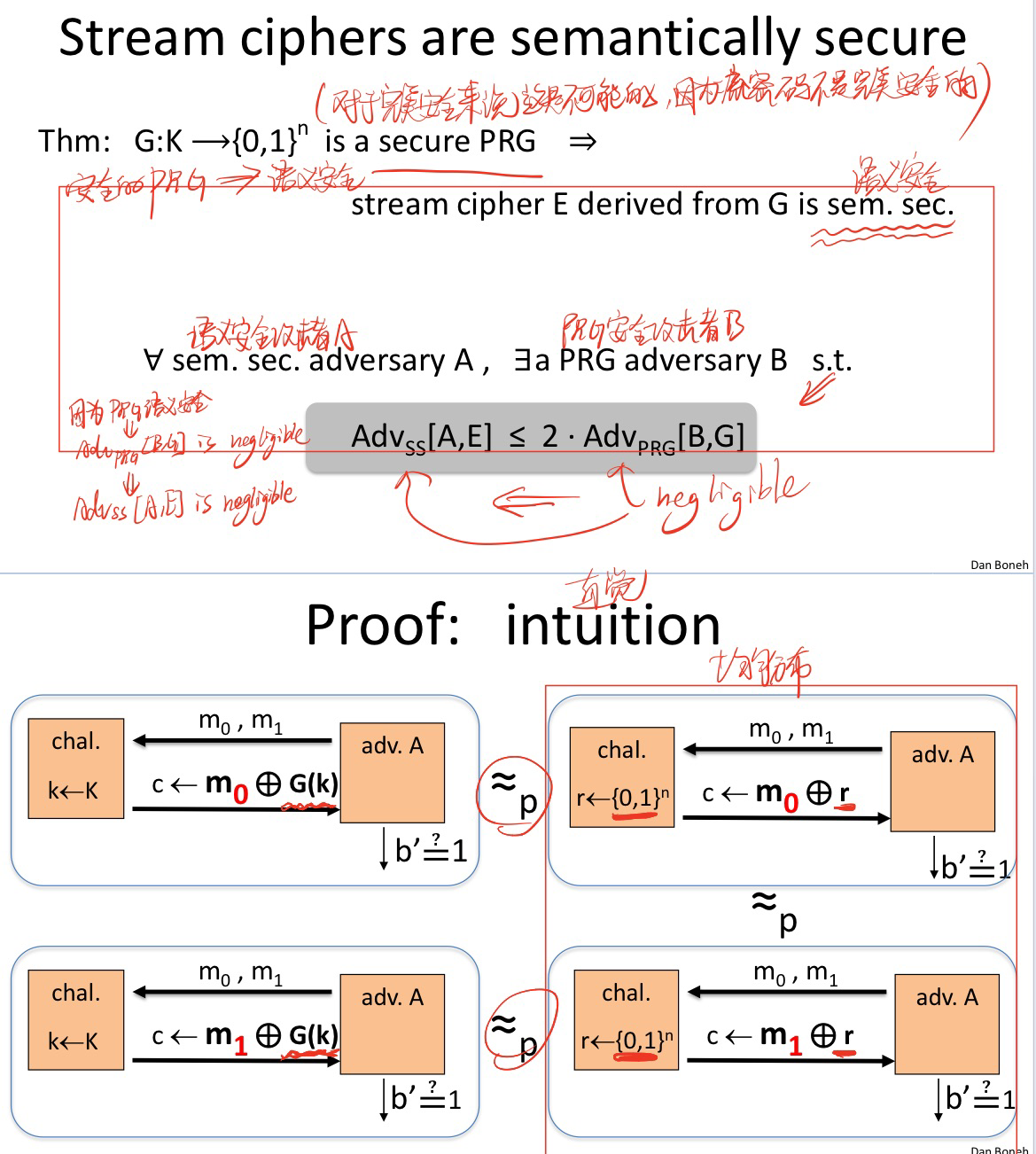
下面开始证明公式: A d v s s [ A , E ] ≤ 2 ∗ A d v P R G [ B , G ] Adv_{ss}[A,E] \le 2 * Adv_{PRG}[B,G] Advss[A,E]≤2∗AdvPRG[B,G]
从直观的思路中可以看出,此公式成立则流密码的语义安全性可得证
证明前,公式化变量的假设:
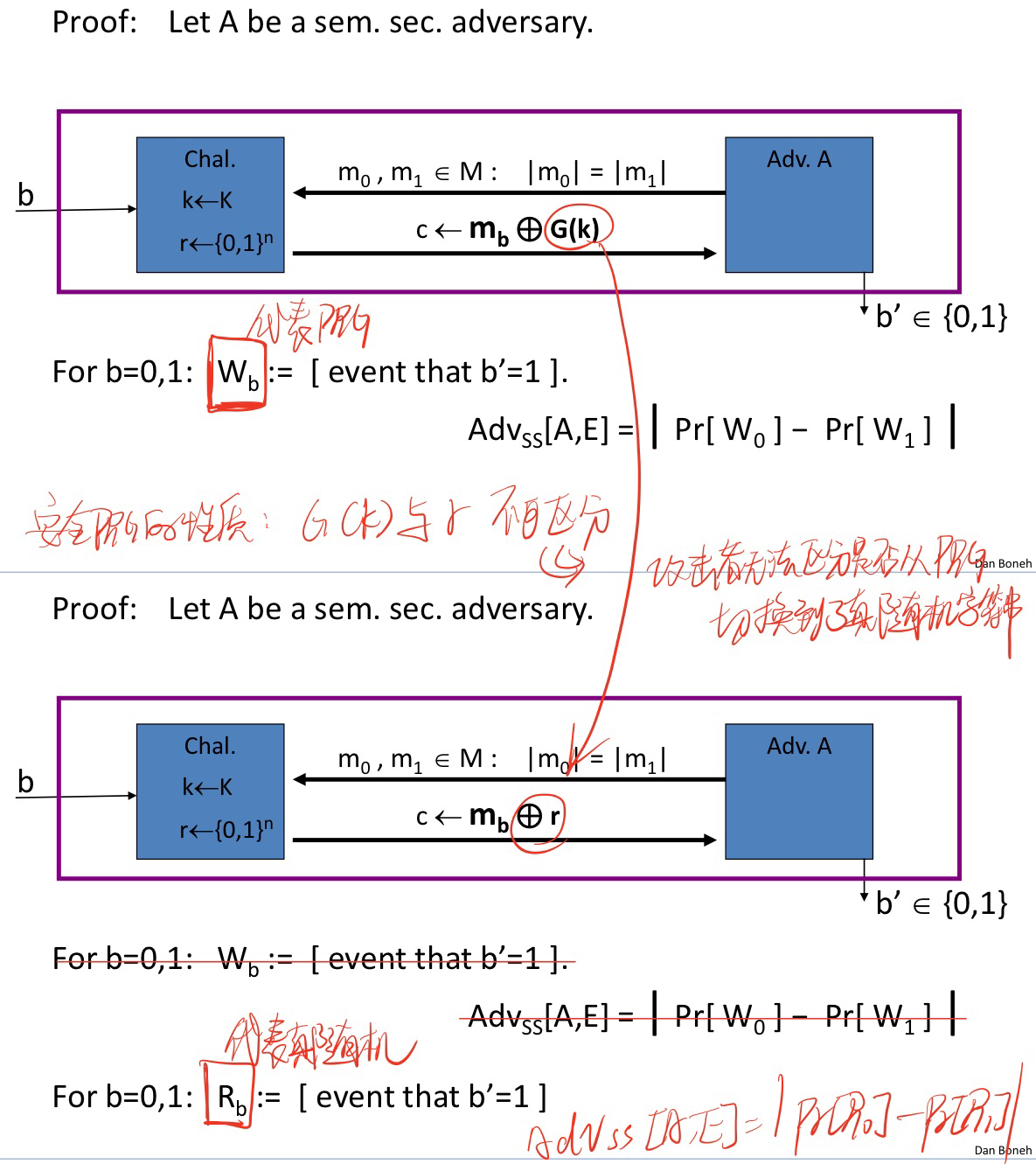
提出两个论断则可证明上述公式的正确性:
(论断一根据OTP的安全定义已证明,论断二的证明见下方)

至此完整的证明了流密码是语义安全的密码