题意:把给出的n条线段分成k组,使得每组都保证线段有交,或者是一条线。求最后所有k个组交的长度的和。
想做这道题首先要搞清楚几个点:
1,怎么处理复杂关系的区间。
2,知道是dp之后,怎么推转移方程。
3,如何进行优化。
这里面最难想的可能是第一个点了。因为在做这道题前我已经假定这道题是dp题,于是我首先试着写一下转移方程
for(int i = 1;i <= 0;i++) //n person
for(int j = 1;j <= k j++) //k group
for(int l = 1;l < i;l++) //from l to i
dp[i][j] = trans{
dp[l][j-1] + val}
朴素dp的大体形式就是这样,由于dp之间的转移是根据区间相差1的转移,所以根据题目规定区间内必有交可以确定,val即a[l].r-a[i].l,即 l 与 i之间可以获得的贡献值。
要进行这样的转移,那原始的数据必定不满足,所以我们处理一下原数据。
即根据以下顺序对线段进行排序。(从别人那新学的排序写法)
sort(a + 1, a + 1 + n, [&](node k1, node k2) {
if (k1.r == k2.r) return k1.l > k2.l; //右区间相同,区间逐渐变大
return k1.r < k2.r;
});
排完序可以得到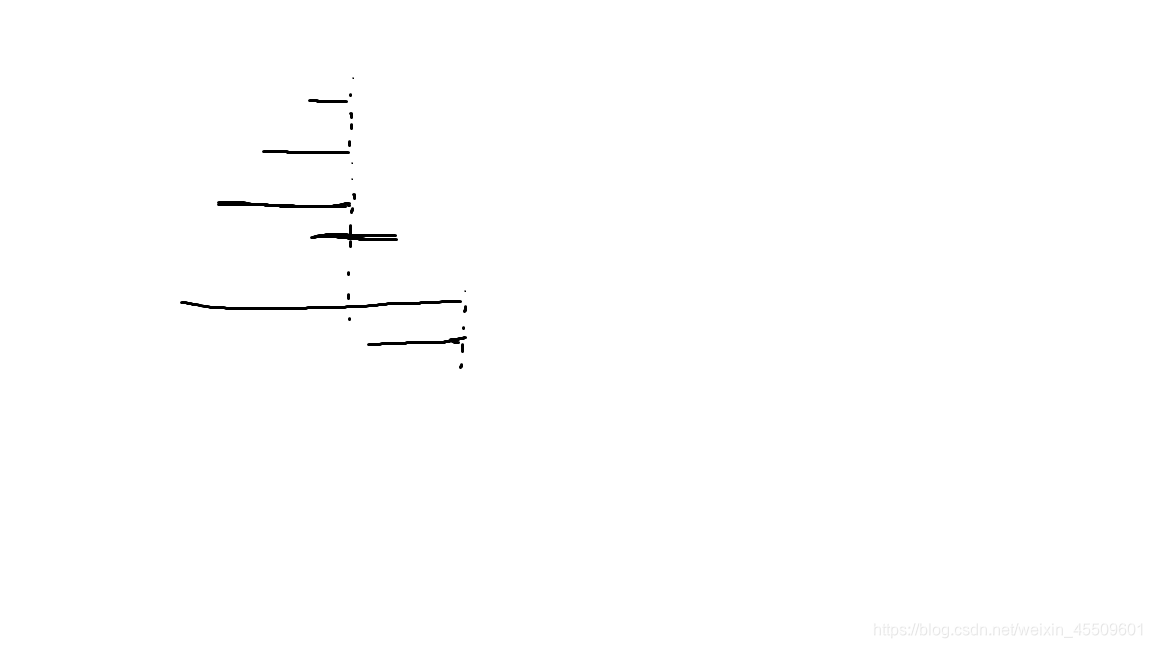
我们可以发现一些能完全包含出现过的线段的,根本没必要放在同一个集合里,放了也可以但是没有贡献。这为我们提供了方便。最后计算答案时,我们不用管这些大集合,因为他们可以任意的放入有完全包含关系的集合,也可以另开集合做为贡献。所以我们剃掉这些包含其他线的大集合,放入一个容器。
接下来我们获得了所有的小线段,开始进行dp,朴素dp肯定会tle,我们发现线段之间会不会出现没有交集的情况我们恰好可以用单调队列模拟,若没有交集则弹出头部,直到再次出现交集,我们在那个点转移。然后就是经典的单调队列优化,每次转移完,把尾部更新。
dp[i][l] = dp[q[head]][l - 1] + seg[q[head] + 1].r - seg[i].l
这里我们可以进行移项,下标带 i 归一类,即
dp[i][l] + seg[i].l - (dp[q[head]][l - 1] + seg[q[head] + 1].r)
将这个值与队尾比较即可。
最后统计答案为缺少集合的答案加上之前大区间的前几个最大值就行。
#include "bits/stdc++.h"
using namespace std;
const int N = 5e3 + 10;
int cnt;
int head[N];
struct node {
int l, r;
};
node a[N];
vector<node> seg;
vector<int> oth;
int dp[N][N];
int q[N];
int main() {
// freopen("in.txt", "r", stdin);
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; ++i) {
cin >> a[i].l >> a[i].r;
}
sort(a + 1, a + 1 + n, [&](node k1, node k2) {
if (k1.r == k2.r) return k1.l > k2.l; //右区间相同,区间逐渐变大
return k1.r < k2.r;
});
seg.push_back(node{
0, 0});
for (int i = 1; i <= n; ++i) {
int flag = 1;
for (int j =1; j < i; ++j) {
//遍历,因为可能出现下一个右端点大,但左端点也大的,而后一个右端点大并且左端点也小于a[i]的
if (a[i].r >= a[j].r && a[i].l <= a[j].l) {
flag = 0;
break;
}
}
if (flag) seg.push_back(a[i]);
else oth.push_back(a[i].r - a[i].l);
}
sort(oth.begin(), oth.end(), [&](int a, int b) {
return a > b;
});
memset(dp, 0xcf, sizeof dp);
dp[0][0] = 0;
for (int l = 1; l <= k; l++) {
int head = 1;
int tail = 0;
for (int i = 0; i <= seg.size() - 1; ++i) {
if (i != 0) {
while (head <= tail && seg[q[head]+1].r <= seg[i].l) head++;
if (head <= tail)
dp[i][l] = dp[q[head]][l - 1] + seg[q[head] + 1].r - seg[i].l;
// cout << l << ' ' << seg[q[head] + 1].r << ' ' << seg[i].l<< endl;
}
while (head <= tail && dp[i][l - 1] + seg[i + 1].r >= dp[q[tail]][l - 1] + seg[q[tail] + 1].r) tail--;
q[++tail] = i;
}
}
int ma = 0;
for (int i = 1; i <= k; ++i) {
int ans = dp[seg.size() - 1][i];
for (int j = 0; j < k - i && j < oth.size(); ++j) {
ans += oth[j];
}
ma = max(ma, ans);
}
cout << ma << endl;
}