5.4 估计、偏差和方差
5.4.1 点估计
点估计是依据样本估计总体分布中所含的未知参数或未知参数的函数。简单的来说,指直接以样本指标来估计总体指标,也叫定值估计。通常它们是总体的某个特征值,如数学期望、方差和相关系数等。点估计问题就是要构造一个只依赖于样本的量,作为未知参数或未知参数的函数的估计值。构造点估计常用的方法是:
①矩估计法,用样本矩估计总体矩
②最大似然估计法。利用样本分布密度构造似然函数来求出参数的最大似然估计。
③最小二乘法。主要用于线性统计模型中的参数估计问题。
④贝叶斯估计法。
1. 矩估计法
矩估计法, 也称“矩法估计”,就是利用样本矩来估计总体中相应的参数。对于随机变量来说,矩是其最广泛,最常用的数字特征,主要有中心矩和原点矩。 由辛钦大数定律知,简单随机样本的原点矩依概率收敛到相应的总体原点矩,这就启发我们想到用样本矩替换总体矩,进而找出未知参数的估计,基于这种思想求估计量的方法称为矩法。用矩法求得的估计称为矩法估计,简称矩估计。最简单的矩估计法是用一阶样本原点矩来估计总体的期望而用二阶样本中心矩来估计总体的方差。
1.1 原点矩与中心距
原点矩: E ( X k ) E(X^k) E(Xk) 中心矩: E ( X − E X ) k E(X-E X)^{k} E(X−EX)k
一阶原点矩就是期望,二阶中心矩就是方差
1.2 原理概述
设总体X的概率密度为 f ( x ; θ 1 , θ 2 , . . . , θ m ) f(x;\theta_1,\theta_2,...,\theta_m) f(x;θ1,θ2,...,θm),其中 θ 1 , θ 2 , . . . , θ m \theta_1,\theta_2,...,\theta_m θ1,θ2,...,θm为未知参数,假定X的前m阶矩 μ k = E ( X k ) ( k = 1 , 2 , . . . , m ) \mu_k=E(X^k)(k=1,2,...,m) μk=E(Xk)(k=1,2,...,m)都存在,他们是 θ 1 , θ 2 , . . . , θ m \theta_1,\theta_2,...,\theta_m θ1,θ2,...,θm的函数,记为 q k ( θ 1 , θ 2 , . . . , θ m ) q_k(\theta_1,\theta_2,...,\theta_m) qk(θ1,θ2,...,θm),即
μ k = ∫ − ∞ + ∞ x k f ( x ; θ 1 , θ 2 , ⋯ , θ m ) d x = q k ( θ 1 , θ 2 , ⋯ , θ m ) \mu_{k}=\int_{-\infty}^{+\infty} x^{k} f\left(x ; \theta_{1}, \theta_{2}, \cdots, \theta_{m}\right) \mathrm{d} x=q_{k}\left(\theta_{1}, \theta_{2}, \cdots, \theta_{m}\right) μk=∫−∞+∞xkf(x;θ1,θ2,⋯,θm)dx=qk(θ1,θ2,⋯,θm)
从此方程(组)可解出
θ j = h j ( μ 1 , μ 2 , ⋯ , μ m ) , j = 1 , 2 , ⋯ , m \theta_{j}=h_{j}\left(\mu_{1}, \mu_{2}, \cdots, \mu_{m}\right), \quad j=1,2, \cdots, m θj=hj(μ1,μ2,⋯,μm),j=1,2,⋯,m
那么,当 μ 1 , μ 2 , ⋯ , μ m \mu_{1}, \mu_{2}, \cdots, \mu_{m} μ1,μ2,⋯,μm均未知时,
θ ^ j = h j ( a 1 , a 2 , ⋯ , a m ) , j = 1 , 2 , ⋯ , m \hat{\theta}_{j} = h_{j}\left(a_{1}, a_{2}, \cdots, a_{m}\right), \quad j=1,2, \cdots, m θ^j=hj(a1,a2,⋯,am),j=1,2,⋯,m
就是 θ j \theta_j θj的矩估计,其中 a k = 1 n ∑ i = 1 n X i k a_k =\frac{1}{n}\sum_{i=1}^{n}X_{i}^{k} ak=n1∑i=1nXik
1.3 应用实例
设总体X的概率密度为 f ( x ; θ ) = { 1 θ , 0 ⩽ x ⩽ θ , θ > 0 0 , 其他. f(x ; \theta)=\left\{\begin{array}{ll} \frac{1}{\theta}, & 0 \leqslant x \leqslant \theta, \quad \theta>0 \\ 0, & \text { 其他. } \end{array}\right. f(x;θ)={ θ1,0,0⩽x⩽θ,θ>0 其他. ,试求未知参数 θ \theta θ的矩估计
解:因为只有一个参数,所以只需要一个方程,从而只需要一阶矩即可

1、先求总体矩
μ 1 = E X = ∫ 0 θ x 1 θ d x = θ / 2 \mu_1 = EX = \int_{0}^{\theta}x\frac{1}{\theta}dx = \theta/2 μ1=EX=∫0θxθ1dx=θ/2
2、将 θ \theta θ用总体矩表示
θ = 2 μ 1 \theta = 2\mu_1 θ=2μ1
3、将总体矩替换为样本矩
所以 θ ^ = 2 a 1 = 2 X ˉ \hat{\theta} = 2a_1 = 2\bar{X} θ^=2a1=2Xˉ
2. 最大似然估计法
2.1 简单随机样本
简单随机样本是抽样技术的基本概念之一,是指抽样的数据,不但是随机变量,而且相互独立,遵从同一分布(即同总体所遵从的分布)。
2.2 原理概述
最大似然估计本质上是通过找到是结果概率最大化的参数值作为参数的估计
在简单随机样本的条件下,由于样本之间的独立性,可以得到下式
f ( x ; θ 1 , θ 2 , ⋯ , θ m ) = ∏ i = 1 n f ( x i ; θ 1 , θ 2 , ⋯ , θ m ) f\left(x ; \theta_{1}, \theta_{2}, \cdots, \theta_{m}\right) = \prod_{i=1}^{n} f\left(x_i; \theta_{1}, \theta_{2}, \cdots, \theta_{m}\right) f(x;θ1,θ2,⋯,θm)=i=1∏nf(xi;θ1,θ2,⋯,θm)
L = L ( θ 1 , θ 2 , ⋯ , θ m ) = ∏ i = 1 n f ( x i ; θ 1 , θ 2 , ⋯ , θ m ) L = L(\theta_{1}, \theta_{2}, \cdots, \theta_{m}) = \prod_{i=1}^{n} f\left(x_i; \theta_{1}, \theta_{2}, \cdots, \theta_{m}\right) L=L(θ1,θ2,⋯,θm)=i=1∏nf(xi;θ1,θ2,⋯,θm)
L ( θ ^ 1 , θ ^ 2 , ⋯ , θ ^ m ) = max θ 1 , . . . , θ m L ( θ 1 , θ 2 , ⋯ , θ m ) L(\hat\theta_{1}, \hat\theta_{2}, \cdots, \hat\theta_{m}) = \max_{\theta_{1},..., \theta_{m}}L(\theta_{1}, \theta_{2}, \cdots, \theta_{m}) L(θ^1,θ^2,⋯,θ^m)=θ1,...,θmmaxL(θ1,θ2,⋯,θm)
求 L L L最大值的过程就是取对数,求偏导,令偏导数为0,最终得到 θ \theta θ的估计
2.3 应用实例
设总体X服从指数分布 f ( x ; λ ) = { λ e − λ x , x > 0 , λ > 0 0 , x ≤ 0 f(x ; \lambda)=\left\{\begin{array}{ll} \lambda e^{-\lambda x}, & x>0, \lambda>0 \\ 0, & x \le 0 \end{array}\right. f(x;λ)={
λe−λx,0,x>0,λ>0x≤0,求未知参数 λ \lambda λ的极大似然估计
L ( λ ) = ∏ i = 1 n ( λ e − λ x i ) = λ n e − λ ∑ i = 1 n x i L(\lambda)=\prod_{i=1}^{n}\left(\lambda \mathrm{e}^{-\lambda x_{i}}\right)=\lambda^{n} \mathrm{e}^{-\lambda} \sum_{i=1}^{n} x_{i} L(λ)=i=1∏n(λe−λxi)=λne−λi=1∑nxi
ln L ( λ ) = n ln λ − λ ∑ i = 1 n x i \ln L(\lambda)=n \ln \lambda-\lambda \sum_{i=1}^{n} x_{i} lnL(λ)=nlnλ−λi=1∑nxi
dln L ( λ ) d λ = n λ − ∑ i = 1 n x i = 0 \frac{\operatorname{dln} L(\lambda)}{\mathrm{d} \lambda}=\frac{n}{\lambda}-\sum_{i=1}^{n} x_{i}=0 dλdlnL(λ)=λn−i=1∑nxi=0
从而解得 λ \lambda λ的极大似然估计如下
λ ^ = 1 X ˉ \hat \lambda = \frac{1}{\bar X} λ^=Xˉ1
5.4.2 偏差
评估一个估计量的好坏,需要有一个衡量的准则或标准,包括偏差在内,以下介绍三种标准
无偏性
无偏性考虑偏差
偏差: b i a s ( θ ^ ) = E ( θ ^ ) − θ bias(\hat\theta)= E(\hat\theta)-\theta bias(θ^)=E(θ^)−θ
无偏: 偏差为0,即 E ( θ ^ ) = θ E(\hat\theta)=\theta E(θ^)=θ
虽然无偏性只表示平均误差为零,但从实际应用的角度看无偏估计的意义还在于,如果适用这一个估计量 θ ^ ( X 1 , X 2 , . . . , X n ) \hat\theta(X_1,X_2,...,X_n) θ^(X1,X2,...,Xn)反复计算出N个估计值 θ ^ 1 , θ ^ 2 , . . . , θ ^ N \hat\theta_1,\hat\theta_2,...,\hat\theta_N θ^1,θ^2,...,θ^N,那么根据(辛钦)大数定律,当N很大时,它们的平均值
∑ i = 1 N θ ^ N = E ( θ ^ ) = θ ^ \frac{\sum_{i=1}^{N}\hat\theta}{N} = E(\hat\theta) = \hat\theta N∑i=1Nθ^=E(θ^)=θ^
则可以给出非常接近于真值的估计。(辛钦大数定律描述的就是规模足够大时,样本均值趋近于总体期望)
然而,在实际应用中,并非都能进行反复抽样,通常只是由一个容量为n的样本值,根据估计量来计算出一个估计值,就以此作为对未知参数的估计,因此,为了得到更准确的估计值,我们偏向于在无偏估计中选择有较小方差的估计,也就是下面的有效性。
有效性
有效性考虑方差
设 θ ^ = θ ^ ( X 1 , X 2 , . . . , X n ) \hat\theta = \hat\theta(X_1,X2,...,X_n) θ^=θ^(X1,X2,...,Xn)与 θ ^ ′ = θ ^ ′ ( X 1 , X 2 , . . . , X n ) \hat\theta' = \hat\theta'(X_1,X2,...,X_n) θ^′=θ^′(X1,X2,...,Xn)都是 θ \theta θ的无偏估计,如果对任何可能的参数值 θ \theta θ都有
D θ ( θ ^ ) ≤ D θ ( θ ^ ′ ) D_{\theta}(\hat\theta)\le D_\theta(\hat\theta') Dθ(θ^)≤Dθ(θ^′)
且至少对某个参数值 θ 0 \theta_0 θ0使小于号成立,则称 θ ^ \hat\theta θ^ 比 θ ^ ′ \hat\theta' θ^′ 有效
相合性
称估计量 θ ^ = θ ^ ( X 1 , X 2 , . . . , X n ) \hat\theta = \hat\theta(X_1,X2,...,X_n) θ^=θ^(X1,X2,...,Xn)是未知参数 θ \theta θ的相合(或一致)估计量,如果 θ ^ \hat\theta θ^依概率收敛于 θ \theta θ,即对任意的 ε > 0 \varepsilon>0 ε>0,有
lim n → ∞ P ( ∣ θ ^ n − θ ∣ ⩾ ε ) = 0 \lim _{n \rightarrow \infty} P\left(\left|\hat\theta_{n}-\theta\right| \geqslant \varepsilon\right)=0 n→∞limP(∣∣∣θ^n−θ∣∣∣⩾ε)=0
例如,样本原点矩 a k = 1 n ∑ i = 1 n X i k a_k = \frac{1}{n}\sum_{i=1}^{n}X_i^k ak=n1∑i=1nXik是总体原点矩 μ = E X k \mu = EX^k μ=EXk的相合估计(根据大数定律证明)
5.4.3 方差与标准差
我们希望一个估计量的偏差尽可能小,但同时我们也希望估计量比较稳定,即估计量有较小的方差
均值的标准差
SE ( μ ^ m ) = Var [ 1 m ∑ i = 1 m x ( i ) ] = σ m \operatorname{SE}\left(\hat{\mu}_{m}\right)=\sqrt{\operatorname{Var}\left[\frac{1}{m} \sum_{i=1}^{m} x^{(i)}\right]}=\frac{\sigma}{\sqrt{m}} SE(μ^m)=Var[m1i=1∑mx(i)]=mσ
均值的标准差在机器学习实验中非常有用。我们通常用测试集样本的误差均值来估计泛化误差。测试集中样本的数量决定了这个估计的精确度。
5.4.4 权衡偏差和方差以最小化均方误差
交叉验证
请见 交叉验证,K折交叉验证的偏差和方差分析 - 简书 (jianshu.com)
均方误差(MSE)
推导过程见 关于参数的均方误差与偏差和方差之间的关系推导 - 知乎 (zhihu.com),值得注意的是 θ \boldsymbol\theta θ是一个常数
M S E = E [ ( θ ^ m − θ ) 2 ] = B i a s ( θ ^ m ) 2 + V a r ( θ m ) MSE = E[(\hat\theta_m-\theta)^2] = Bias(\hat\theta_m)^2+Var(\theta_m) MSE=E[(θ^m−θ)2]=Bias(θ^m)2+Var(θm)
偏差与方差的关系
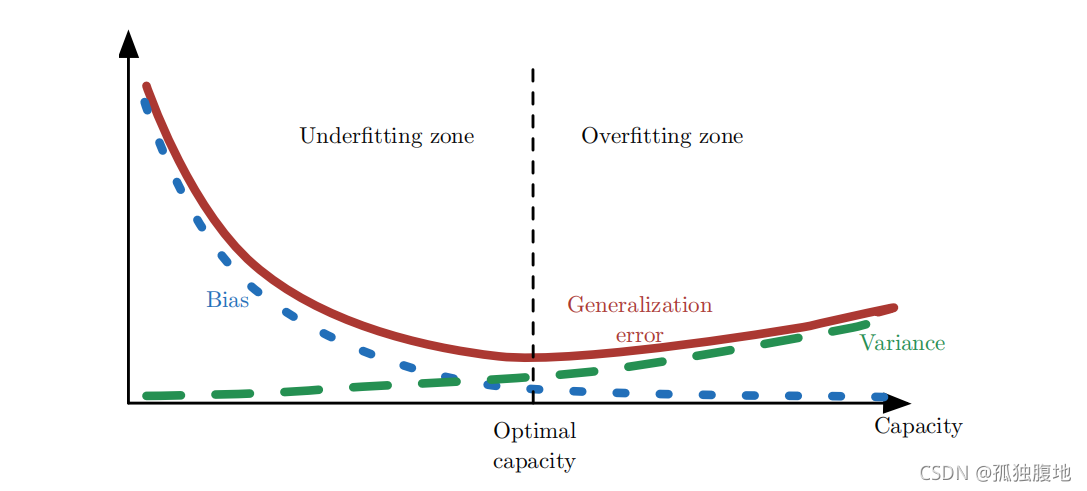
从图中不仅能看到偏差与方差的关系,也能看出模型过拟合往往高方差低偏差,欠拟合往往高偏差低方差
5.4.5 一致性
弱一致性与强一致性

一致性与渐进无偏


上面举的示例没看懂,为什么 E ( θ ^ m ) = θ E(\hat\theta_m) = \theta E(θ^m)=θ ?m下标是什么意思?待解决。。。。。。