-
前言:
因为之前做了一道cf上面的题,需要用到组合数,并且数据过大,于是学习了一下在可能会爆精度的情况下组合数的求法。 -
公式:
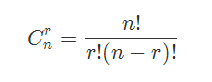
-
普通的算法:
运用公式 C(n, m) = C(n-1, m) + C(n-1, m-1)
注意边界条件:C(i, 0) = 1; i in range(0, n+1)
代码:
int numTrees(int n) {
vector<vector<long long>> dp(2*n+1, vector<long long>(n+1));
for(int i = 0;i <= 2*n;i++){
dp[i][0] = 1;
}
for(int i = 1;i <= 2*n;i++){
for(int j = 1;j <= min(i, n);j++){
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
cout<<"C "<<i<<" "<<j<<" = "<<dp[i][j]<<endl;
}
}
return dp[2*n][n]/(n+1);
}
- 知识准备
一、欧几里得算法
即我们常说的“辗转相除法”,用来求a和b的最大公约数(greatest common divisor)
int gcd(int a,int b){
return b == 0 ? a : gcd(b,a%b);
}
二、裴蜀定理
裴蜀定理是关于最大公约数的定理。
1、定义:
对于任何整数a b m,方程ax + by = m 有解时,当且仅当 m = gcd(a,b)。注意这里的x和y可能是负数。
2、应用:(下文会讲)
(1)逆元的充分必要条件
(2)扩展欧几里得算法
三、逆元
1、逆元的定义:一整数a对同余之模n逆元 满足以下公式:
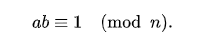
在乘法系中,(a*b) mod n = 1, 则b是a 的逆元。
也就是说,在模n的意义下,如果要 除以一个数a,就相当于乘以a的逆元b。
例如:
(3 * 5)mod 7 = 1,那么5就是3的逆元。那么 求 (6/3)mod 7 = 2,也可以用(6 * 5) mod 7 = 2.
2、逆元的充分必要条件:
一个数有逆元的充分必要条件是 gcd(a,n)= 1,此时逆元唯一存在。
这是根据裴蜀定理得到的。因为 (ab) mod n = 1,可以写成 ab + ny = 1.那么逆元b存在,即 gcd(a,n) = 1.
例如:
(3 * 5)mod 7 = 1 。 可以写成 3 * 5 + 7 * (-2) = 1,满足gcd(3,7) = 1.
3、逆元的应用:
当求解 (a/b) mod m时,由于b过大,可能爆精度。
在求组合数时,根据上文的公式
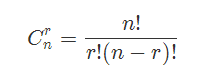
分子r! 以及 (n-r)!,可以转化为他们的逆元,并与n!做乘法。
4、如何求逆元
(一)费马小定理求逆元
若a是整数,p是质数,并且a不是p的倍数,则
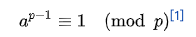
这个公式左边 a^p-1 可以写成 a * a ^p-2。 那么显然, a ^p-2就是a在mod p的情况下的逆元。
int fastpow(int x,int k){
//快速幂 O(logn)
int num = 1;
while (k) {
if (k & 1) {
num = mul(num,x);
}
x = mul(x,x);
k>>=1;
}
return num;
}
int inv(int x){
//求x的逆元。因为逆元英文inverse element
return fastpow(x,mod-2); // x^mod-2 就是逆元
}
注:上文中的快速幂如果不懂,可以参考以下博文:
https://blog.csdn.net/qq_39763472/article/details/82778727
(二)扩展欧几里得求逆元
扩展欧几里德用于在已知a,b的情况下求解一组x,y,使它们满足裴蜀等式: ax + by = gcd(a, b) = d, d是a和b的最大公约数。
根据上面所说,因为 (ab) mod n = 1,可以写成 ab + ny = 1.那么逆元b存在。则逆元b可以通过扩展欧几里得求出。
void exgcd(ll a, ll b, ll &x, ll &y) //拓展欧几里得算法
{
if(!b) x = 1, y = 0;
else
{
exgcd(b, a % b, y, x);
y -= x * (a / b);
}
}
ll inv(ll a, ll b) //求a对b取模的逆元
{
ll x, y;
exgcd(a, b, x, y);
return (x + b) % b;
}
扩展欧几里得的原理可以参考别的博文,自己也不是很清楚。
- 求组合数
有了上面的所有知识准备,那么可以根据组合数的公式
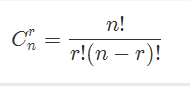
分别求出 r!以及 (n-r)!的逆元,和n的阶乘做乘法即可。
int mul(int x,int y){
//每次乘法取模
return (x*1ll*y)%mod;
}
void cal(){
//生成数据范围内的阶乘 模mod
fac[0] = 1;
for (int i = 1; i < maxn; i++) {
fac[i] = mul(fac[i-1],i);
}
}
int C(int n,int m){
//求组合数
return mul(fac[n],inv(mul(fac[n-m],fac[m])));
}
- 困扰我的CF题
链接:
https://codeforces.com/contest/1312/problem/D
代码:
#include "bits/stdc++.h"
using namespace std;
#define mem(a,b) memset(a,b,sizeof(a))
#define fori(i,l,u) for(int i = l;i < u;i++)
#define pb push_back
typedef long long ll;
const int maxn = 2e5 + 7;
const int mod = 998244353;
int n,m;
int fac[maxn];
int mul(int x,int y){
return (x*1ll*y)%mod;
}
int fastpow(int x,int k){
int num = 1;
while (k) {
if (k & 1) {
num = mul(num,x);
}
x = mul(x,x);
k>>=1;
}
return num;
}
void cal(){
fac[0] = 1;
for (int i = 1; i < maxn; i++) {
fac[i] = mul(fac[i-1],i);
}
}
int inv(int x){
return fastpow(x,mod-2);
}
int C(int n,int m){
return mul(fac[n],inv(mul(fac[n-m],fac[m])));
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
// freopen("1.txt","r",stdin);
cin>>n>>m;
mem(fac,0);
cal();
int ans = 0;
if (n > 2) {
ans = mul(C(m,n-1),mul(n-2,fastpow(2,n-3)));
}
cout<<ans<<endl;
return 0;
}