第1章 线性规划（二）

投资的收益与风险

例 1.9（本题选自1998年全国大学生数学建模竞赛A题）

  市场上有n种资产（如股票、债券等） $S_i(i=1,2,\cdots ,n)$ 供投资者选取，某公司有数额为 $M$ 的一笔相当大的资金可用作一个时期的投资。公司财务分析人员对这 $n$ 种资产进行了评估，估算出在这一时期内购买资产 $S_i$ 的平均收益率为 $r_i$ ，并预测出购买 $S_i$ 的风险损失率为 $q_i$ 。考虑到投资越分散，总的风险越小，公司确定，当用这笔资金购买若干种资产时，总体风险可用所投资的 $S_i$ 中最大的一个风险来度量。
  购买 $S_i$ 要付交易费，费率为 $p_i$ ，并且当购买额不超过给定值 $u_i$ 时，交易额按购买 $u_i$ 计算（不买当然无须付费）。另外，假定同期银行存款率是 $r_0$ （ $r_0=5\%$），且既无交易费有无风险。
  已知 $n=4$ 时的相关数据如表所示。

$s_i$	$r_i/\%$	$q_i/\%$	$p_i/\%$	$u_i/元$
$s_1$	28	2.5	1	103
$s_2$	21	1.5	2	198
$s_3$	23	5.5	4.5	52
$s_4$	25	2.6	6.5	40

  试给该公司设计一种投资组合方案，即用给定的资金 $M$ ，有选择地购买若干种资产或存银行生息，使净收益尽可能大，总体风险尽可能小。

1.问题分析

  这是一个组合投资问题：已知市场上可供投资的 $n+1$ 种资产的平均收益率以及购买资产时产生的交易费用率，设计一种投资组合方案，也就是要将可供投资的资金分成数量不等的 $n+1$ 份分别购买 $n+1$ 种资产。不同类型的资产的平均收益率和风险损失率也各不相同，因此在投资时，要同时兼顾两个目标：投资的净收益和风险。

2.符号说明

$$\begin{array}{rl}& S_i：可供投资的第i种资产，i=0,1,2,\cdots ,n，其中S_0表示存到银行；\\ & x_i：投资到资产S_i的资金数量，i=0,1,2,\cdots ,n，其中x_0表示存到银行的资金数量；\\ & r_i：资产S_i的平均收益率，i=0,1,2,\cdots ,n；\\ & q_i：资产S_i的风险损失率，i=0,1,2,\cdots ,n，其中q_0=0；\\ & p_i：资产S_i的交易费用率，i=0,1,2,\cdots ,n，其中p_0=0；\\ & u_i：资产S_i的投资阈值，i=0,1,2,\cdots ,n。\end{array}$$

3.模型假设

1. 可供投资的资金数额 $M$ 相当大。
2. 投资越分散，总的风险越小，总体风险可用所投资的 $S_i$ 中最大的一个风险来度量。
3. 可供选择的 $n+1$种资产（含银行存款）之间是相互独立的。
4. 每种资产可购买的数量为任意值。
5. 在当前投资周期内，$r_i,q_i,p_i,u_i（i=0,1,\cdots ,n）$固定不变。
6. 不考虑在资产交易过程中产生的其他费用，如股票交易印花税等。

4.模型建立

（1）总体风险用所投资的 $S_i$ 中最大的一个风险来衡量，即
max ⁡ { q i x i ∣ i = 1 , 2 , ⋯   , n } . \max \{ q_ix_i | i = 1,2, \cdots, n \}. max{ qi​xi​∣i=1,2,⋯,n}.
（2）购买 $S_i（i=1,2,\cdots ,n）$所付交易费是一个分段函数，即
$$交易费=\{\begin{array}{r}\begin{array}{rl}& p_i{x}_i,x_i>u_i,\\ & p_i{u}_i,0\le x_i\le u_i.\end{array}\end{array}$$
而题目中给定的定值 $u_i$ （单位：元）相对于总投资 $M$ 很少，$p_i{u}_i$ 更小，这样购买 $S_i$ 的净收益可以简化为 $（r_i-p_i）x_i$ 。

  要使净收益尽可能大，总体风险尽可能小，这是一个多目标规划模型。
  目标函数为
{ max ⁡ ∑ i = 0 n ( r i − p i ) x i , min ⁡ { max ⁡ 1 ≤ i ≤ n { q i x i } } . \left\{ \begin{array}{rcl} \begin{aligned} & \max \sum_{i = 0}^n (r_i - p_i) x_i, \\ & \min \{ \quad \max_{1 \leq i \leq n} \{ q_i x_i\} \quad\}. \end{aligned} \end{array} \right. ⎩⎪⎪⎨⎪⎪⎧​​maxi=0∑n​(ri​−pi​)xi​,min{ 1≤i≤nmax​{ qi​xi​}}.​​
  约束条件为
$$\{\begin{array}{l}{\sum }_{i=0}^n(1+p_i)x_i=M,\\ x_i\ge 0,i=0,1,\cdots ,n.\end{array}$$

模型简化：

① 在实际投资中，投资者承受风险的程度不一样，若给定风险一个界限 $a$ ，使最大的一个风险 $\frac{q_i{x}_i}{M}\le a$，则可找到相应的投资方案

模型一：固定风险水平，优化收益

$$\begin{gathered} \max \sum _{i=0}^n（r_i-p_i）x_i, \\ s.t.\{\begin{array}{llc}& \frac{q_i{x}_i}{M}\le a,& i=1,2,\cdots ,n，\\ & & \\ & {\sum }_{i=0}^n(1+p_i)x_i=M,& \\ & & \\ & x_i\ge 0,& i=0,1,\cdots ,n.\end{array} \end{gathered}$$
② 若投资者希望总盈利至少达到水平 $k$ 以上，在风险最小的情况小寻求相应的投资组合。

模型二：固定盈利水平，极小化风险

min ⁡ { max ⁡ 1 ≤ i ≤ n { q i x i } } ，   s . t . { ∑ i = 0 n ( r i − p i ) x i ≥ k i M ，   ∑ i = 0 n ( 1 + p i ) x i = M ,   x i ≥ 0 , i = 0 , 1 , ⋯   , n . \min \{ \quad \max_{1 \leq i \leq n} \{ q_i x_i\} \quad\}，\\ ~\\ s. t. \begin{cases} & \sum_{i = 0}^n (r_i - p_i) x_i \geq k_i M，\\ ~\\ & \sum_{i = 0}^n (1 + p_i) x_i = M,\\ ~\\ & x_i \geq 0, &i = 0,1, \cdots, n.\\ \end{cases} min{ 1≤i≤nmax​{ qi​xi​}}， s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​  ​∑i=0n​(ri​−pi​)xi​≥ki​M，∑i=0n​(1+pi​)xi​=M,xi​≥0,​i=0,1,⋯,n.​
③ 投资者在权衡资产风险和预期收益两方面时，希望选择一个令自己满意的投资组合。因此对风险。收益分别赋予权重 $w(0\le w\le 1)$ 和 $(1-w)$，$w$ 称为投资偏好系数。

模型三：两个目标函数加权求和

min ⁡ w { max ⁡ 1 ≤ i ≤ n { q i x i } } − ( 1 − w ) ∑ i = 0 n ( r i − p i ) x i ，   s . t . { ∑ i = 0 n ( 1 + p i ) x i = M ,   x i ≥ 0 , i = 0 , 1 , ⋯   , n . \min \quad w\{ \max_{1 \leq i \leq n} \{ q_i x_i\} \} - (1 - w)\sum_{i = 0}^n (r_i - p_i) x_i ，\\ ~\\ s. t. \begin{cases} & \sum_{i = 0}^n (1 + p_i) x_i = M,\\ ~\\ & x_i \geq 0, &i = 0,1, \cdots, n.\\ \end{cases} minw{ 1≤i≤nmax​{ qi​xi​}}−(1−w)i=0∑n​(ri​−pi​)xi​， s.t.⎩⎪⎨⎪⎧​ ​∑i=0n​(1+pi​)xi​=M,xi​≥0,​i=0,1,⋯,n.​

5.模型的求解与分析（含python、matlab代码）

不妨设 $M=10000$ 元。

模型一

模型一为
$$\begin{gathered} \max f=[0.05,0.27,0.19,0.185,0.185]\cdot [x_0,x_1,x_2,x_3,x_4{]}^T， \\ s.t.\{\begin{array}{ll}& x_0+1.01x_1+1.02x_2+1.045x_3+1.065x_4=M,\\ & 0.025x_1\le aM,\\ & 0.015x_2\le aM,\\ & 0.055x_3\le aM,\\ & 0.026x_4\le aM,\\ & x_i\ge 0(i=0,1,2,\cdots ,4).\end{array} \end{gathered}$$
matlab程序：

prob = optimproblem('ObjectiveSense', 'max');
x = optimvar('x', 5, 1, 'LowerBound', 0);
c = [0.05,0.27,0.19,0.185,0.185];
Aeq = [1,1.01, 1.02, 1.045, 1.065]; %等号约束矩阵
prob.Objective = c * x; M = 10000;
prob.Constraints.con1 = Aeq * x == M;
q = [0.025,0.015, 0.055,0.026]';
a =0;aa = [];QQ=[];XX=[];
hold on
while a<0.05
prob.Constraints.con2 = q.*x(2:end) <= a*M;
[sol,Q,flag,out] = solve(prob)
aa = [aa;a];QQ=[QQ,Q];
XX=[XX;sol.x'];a=a+0.001;
end
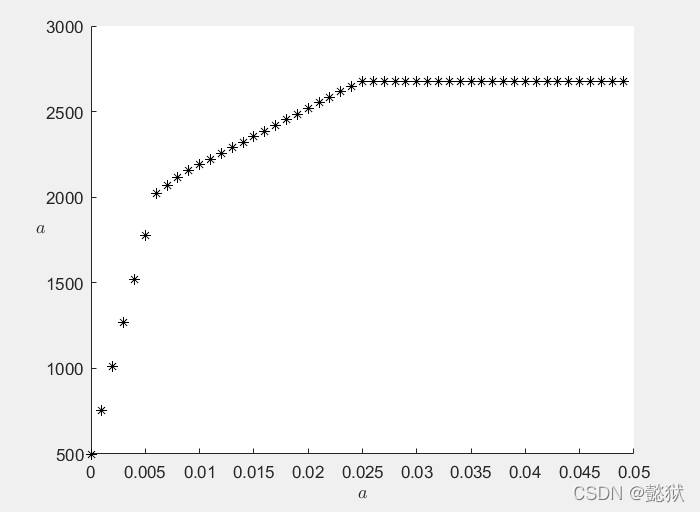
plot(aa, QQ, '*k')
xlabel('$a$','Interpreter','Latex')
ylabel('$a$','Interpreter','Latex', 'Rotation', 0)

import matplotlib.pyplot as plt
from scipy import optimize
import numpy as np

c = np.array([0.05, 0.27, 0.19, 0.185, 0.185])
A = np.array([
    [0, 0.025, 0, 0, 0],
    [0, 0, 0.015, 0, 0],
    [0, 0, 0, 0.055, 0],
    [0, 0, 0, 0, 0.026]
])
a = 0
M = 10000
b = np.array([M, M, M, M])

Aeq = np.array([[1, 1.01, 1.02, 1.045, 1.065]])
Beq = np.array([M])
Q_history = []
a_history = []
while a < 0.05:
    res = optimize.linprog(-c, A_ub=A, b_ub=a * b, A_eq=Aeq, b_eq=Beq, bounds=([0, None]), method='revised simplex')
    a_history.append(a)
    Q_history.append(-res.fun)
    a = a + 0.001

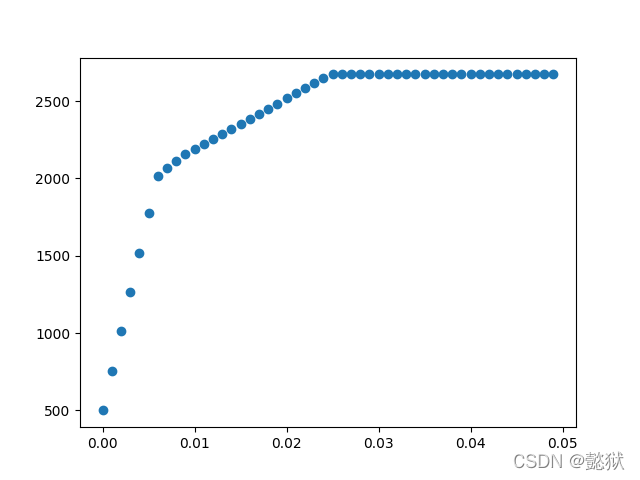
plt.scatter(a_history, Q_history)
plt.show()

模型二

模型二为
min ⁡ { max ⁡ 1 ≤ i ≤ n { q i x i } } ，   s . t . { ∑ i = 0 n ( r i − p i ) x i ≥ k i M ，   ∑ i = 0 n ( 1 + p i ) x i = M ,   x i ≥ 0 , i = 0 , 1 , ⋯   , n . \min \{ \quad \max_{1 \leq i \leq n} \{ q_i x_i\} \quad\}，\\ ~\\ s. t. \begin{cases} & \sum_{i = 0}^n (r_i - p_i) x_i \geq k_i M，\\ ~\\ & \sum_{i = 0}^n (1 + p_i) x_i = M,\\ ~\\ & x_i \geq 0, &i = 0,1, \cdots, n.\\ \end{cases} min{ 1≤i≤nmax​{ qi​xi​}}， s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​  ​∑i=0n​(ri​−pi​)xi​≥ki​M，∑i=0n​(1+pi​)xi​=M,xi​≥0,​i=0,1,⋯,n.​
  在具体求解时，需要将目标函数具体化，引进变量 x n + 1 = max ⁡ 1 ≤ i ≤ n { q x x i } x_{n+1} = \max_{1 \leq i \leq n} \{ q_x x_i\} xn+1​=max1≤i≤n​{ qx​xi​} ，则模型可线性化为
$$\begin{gathered} \min x_{n+1}， \\ s.t.\{\begin{array}{llc}& q_i{x}_i\le x_{n+1,}& \\ & & \\ & {\sum }_{i=0}^n(r_i-p_i)x_i\ge k_{i}M，& \\ & & \\ & {\sum }_{i=0}^n(1+p_i)x_i=M,& \\ & & \\ & x_i\ge 0,& i=0,1,\cdots ,n.\end{array} \end{gathered}$$
python代码

import matplotlib.pyplot as plt
from scipy import optimize
import numpy as np

c = np.array([0, 0, 0, 0, 0, 1])
r_i = np.array([0.05, 0.28, 0.21, 0.23, 0.25, 0])
p_i = np.array([0, 0.01, 0.02, 0.045, 0.065, 0])
M = 10000
k = 0

A = np.array([
    [-0.05, -0.27, -0.19, -0.185, -0.185, 0],
    [0, 0, 0, 0, 0, -1],
    [0, 0.025, 0, 0, 0, -1],
    [0, 0, 0.015, 0, 0, -1],
    [0, 0, 0, 0.055, 0, -1],
    [0, 0, 0, 0, 0.026, -1]
])
b = np.array([-M, 0, 0, 0, 0, 0])

Aeq = np.array([[1, 1.01, 1.02, 1.045, 1.065, 0]])
Beq = np.array([M])

while k < 0.3:
    res = optimize.linprog(c, A_ub=A, b_ub=k * b, A_eq=Aeq, b_eq=Beq, bounds=([0, None]), method='revised simplex')
    k = k + 0.001

就提供一下求解的部分，分析的自己写写看吧。

模型三就是将模型一二综合起来，就不写了。