第十一届蓝桥杯 2020年国赛真题 (Java 大学A组)

---

  做套题打发下时间。

---

#A 合数个数

本题总分：$5$ 分

---

问题描述

  一个数如果除了 $1$ 和自己还有其他约数，则称为一个合数。例如：$1,2,3$ 不是合数，$4,6$ 是合数。

  请问从 $1$ 到 $2020$ 一共有多少个合数。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1317

---

埃氏筛

---

public class Test {
    
    

    static int N = 2020, ans = 0;

    public static void main(String[] args) {
    
    
        boolean[] factor = new boolean[N + 1];
        for (int i = 2; i <= N; i++)
            if (!factor[i])
                for (int j = i << 1; j <= N; j += i) factor[j] = true;
            else ans++;
        System.out.println(ans);
    }
}

  无他，签到尔。

---

---

#B 含 2 天数

本题总分：$5$ 分

---

问题描述

  小蓝特别喜欢 $2$，今年是公元 $2020$ 年，他特别高兴，因为每天日历上都可以看到 $2$。

  如果日历中只显示年月日，请问从公元 $1900$ 年 $1$ 月 $1$ 日到公元 $9999$ 年 $12$ 月 $31$ 日，一共有多少天日历上包含 $2$。即有多少天中年月日的数位中包含数字 $2$。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1994240

---

所以 Java 是世界上最好的语言

---

import java.time.LocalDate;

public class Test {
    
    

    static int ans = 0;

    public static void main(String[] args) {
    
    
        LocalDate start = LocalDate.of(1900, 1, 1);
        LocalDate end = LocalDate.of(9999, 12, 31);
        while (start.compareTo(end) <= 0) {
    
    
            if (start.toString().contains("2")) ans++;
            start = start.plusDays(1);
        }
        System.out.println(ans);
    }
}

---

归纳法

---

  首先答案可以分为两部分，

  一、年份数位中包含数字 $2$ 的个数。

  二、年份数位中不含数字 $2$ 的个数。

  两部分分别计算，而对于闰年，因为闰月为 $2$ 月份，也就是包含闰月的时间一定包含 $2$，故我们将 $1900$ 至 $9999$ 之间所有年份都视为平年，再在答案上累加一个闰年数即可。

  现在来讨论一个平年中，月日部分某数位包含 $2$ 的情况，我们先将 $2$、$12$ 分离出来，计为 $28+31$，其余的部分因为 $30$ 、$31$ 日以及月份都不包含 $2$，于是我们将 $1\sim 9$ 日、$10\sim 19$ 日、$20\sim 29$ 日中包含的 $2$ 的月份累加为 $1＋1+10$，对于一个平年的日月部分，包含有 $2$ 的个数为 $179$。

  然后讨论 $1900\sim 9999$ 中包含有 $2$ 的年份，对此可以拆分为 $100k\sim 100k+99$，$k\in [19,99]$ 的若干个小区间，再从中剔除 k = { [ 20 , 29 ] , 32 , 42 , ⋯   , 92 } k = \{[20,29],32,42,\cdots,92\} k={ [20,29],32,42,⋯,92} 这 $17$ 个区间，接下来的区间中，个十位包含 $2$ 的有 $100k+2,100k+12,100k+[20,29],\cdots ,100k+92$ 即 $19$ 个，综上年份包含 $2$ 的年份个数为 $\frac{19}{100}(9999-1900+1-1700)+1700=1216$，不包含的则为 $9999-1900+1-1216=5184$。

  最后就是统计 $1900$ 至 $9999$ 之间的闰年，根据容斥原理，设 $f_{year}$ 为 $1$ 至 $year$ 年之间的闰年数，则 $f_{year}=\lfloor \frac{year}{4}\rfloor -\lfloor \frac{year}{100}\rfloor +\lfloor \frac{year}{400}\rfloor$，给定年份之间的闰年数为 $f_{9999}-f_{1899}=1964$。

  综上，答案为 $1216\times 365+5184\times 179+1964=1994240$。

  由于网络上不依赖 $\mathrm{A}\mathrm{P}\mathrm{I}$ 实现的程序完成题目所述功能的程序有很多，这里便不再费这个精力去编写了。

---

#C 本质上升序列

本题总分：$10$ 分

---

问题描述

  小蓝特别喜欢单调递增的事物。
  在一个字符串中，如果取出若干个字符，将这些字符按照在字符串中的顺序排列后是单调递增的，则成为这个字符串中的一个单调递增子序列。
  例如，在字符串 $\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{q}\mathrm{i}\mathrm{a}\mathrm{o}$ 中，如果取出字符 $\mathrm{n}$ 和 $\mathrm{q}$，则 $\mathrm{n}\mathrm{q}$ 组成一个单调递增子序列。类似的单调递增子序列还有 $\mathrm{l}\mathrm{n}\mathrm{q}$、$\mathrm{i}$、$\mathrm{a}\mathrm{n}\mathrm{o}$ 等等。
  小蓝发现，有些子序列虽然位置不同，但是字符序列是一样的，例如取第二个字符和最后一个字符可以取到 $\mathrm{a}\mathrm{o}$，取最后两个字符也可以取到 $\mathrm{a}\mathrm{o}$。
  小蓝认为他们并没有本质不同。
  对于一个字符串，小蓝想知道，本质不同的递增子序列有多少个？
  例如，对于字符串 $\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{q}\mathrm{i}\mathrm{a}\mathrm{o}$，本质不同的递增子序列有 $21$ 个。它们分别是 $\mathrm{l}$、$\mathrm{a}$、$\mathrm{n}$、$\mathrm{q}$、$\mathrm{i}$、$\mathrm{o}$、$\mathrm{l}\mathrm{n}$、$\mathrm{a}\mathrm{n}$、$\mathrm{l}\mathrm{q}$、$\mathrm{a}\mathrm{q}$、$\mathrm{n}\mathrm{q}$、$\mathrm{a}\mathrm{i}$、$\mathrm{l}\mathrm{o}$、$\mathrm{a}\mathrm{o}$、$\mathrm{n}\mathrm{o}$、$\mathrm{i}\mathrm{o}$、$\mathrm{l}\mathrm{n}\mathrm{q}$、$\mathrm{a}\mathrm{n}\mathrm{q}$、$\mathrm{l}\mathrm{n}\mathrm{o}$、$\mathrm{a}\mathrm{n}\mathrm{o}$、$\mathrm{a}\mathrm{i}\mathrm{o}$。
  请问对于以下字符串（共 $200$ 个小写英文字母，分四行显示）：（如果你把以下文字复制到文本文件中，请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt，内容与下面的文本相同）

tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl

  本质不同的递增子序列有多少个？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

3616159

---

动态规划

---

  首先考虑上升子序列问题，即子串可以相同的情况。

  设 $f_i$ 为以字符串 $S[1,n]$ 第 $i$ 个字符结尾的最长递增子序列的个数，则总个数为 ${\sum }_{i=1}^n{f}_i$，状态转移方程为 $f_i={\sum }_{j=1}^{i-1}{f}_j(S[i]>S[j])$。

  为了避免出现重复子串，考虑互斥的划分方式，

  有状态 $f_{i,c}$ 表示到第 $i$ 个字符为止，以 $c$ 结尾的本质不同子串的个数为多少，显然答案为 ${\sum }_c{f}_{n,c}$。

  可是如何保证不重不漏呢？

  对于 $c\ne S[i]$，显然有 $f_{i,c}=f_{i-1,c}$，而对于 $c=S[i]$ 的情况，考虑重新统计即 $f_{i,c}={\sum }_{c^{\prime }=1}^{c-1}{f}_{i-1,c^{\prime }}$，不重是做到了，即可不重不漏。

   证明半天证明了一坨屎，其实可以用反证法，但反证太无聊了。

import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.util.Scanner;

public class Test {
    
    

    public static void main(String[] args) {
    
      new Test().run(); }

    void run() {
    
    
        try(Scanner in = new Scanner(new FileInputStream("inc.txt"))) {
    
    
            String str = "";
            while (in.hasNext()) str = str + in.nextLine();
            int n = str.length(), ans = 0;
            int[][] dp = new int[n + 1][128];
            for (int i = 1; i <= n; i++) {
    
    
                for (char c = 'a'; c <= 'z'; c++) dp[i][c] = dp[i - 1][c];
                int now = str.charAt(i - 1);
                dp[i][now] = 1;
                for (int c = now - 1; c >= 'a'; c--) dp[i][now] += dp[i - 1][c];
            }
            for (char c = 'a'; c <= 'z'; c++) ans += dp[n][c];
            System.out.println(ans);
        } catch (FileNotFoundException e) {
    
    
            e.printStackTrace();
        }
    }
}

  不过数据规模也不大，开个线程暴搜也能完事。

---

#D 咫尺天涯

本题总分：$10$ 分

---

  皮亚诺曲线是一条平面内的曲线。

  下图给出了皮亚诺曲线的 $1$ 阶情形，它是从左下角出发，经过一个 $3\times 3$ 的方格中的每一个格子，最终到达右上角的一条曲线。

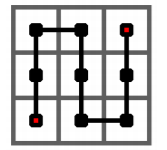
  设每个格子的边长为 $1$，在上图中，有的相邻的方格（四相邻）在皮亚诺曲线中也是相邻的，在皮亚诺曲线上的距离是 $1$，有的相邻的方格在皮亚诺曲线中不相邻，距离大于 $1$。

  例如，正中间方格的上下两格都与它在皮亚诺曲线上相邻，距离为 $1$，左右两格都与它在皮亚诺曲线上不相邻，距离为 $3$。

  下图给出了皮亚诺曲线的 $2$ 阶情形，它是经过一个 $3^2\times 3^2$ 的方格中的每一个格子的一条曲线。它是将 $1$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

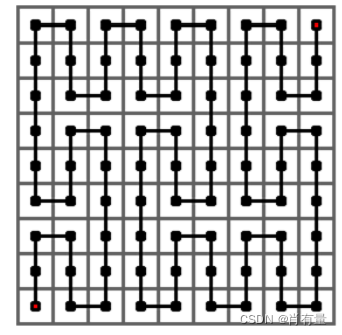
  下图给出了皮亚诺曲线的 $3$ 阶情形，它是经过一个 $3^3\times 3^3$ 的方格中的每一个格子的一条曲线。它是将 $2$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

  皮亚诺曲线总是从左下角开始出发，最终到达右上角。

  小蓝对于相邻的方格在皮亚诺曲线上的相邻关系很好奇，他想知道相邻的方格在曲线上的距离之和是多少。

  例如，对于 $1$ 阶皮亚诺曲线，距离和是 $24$，有 $8$ 对相邻的方格距离为 $1$，$2$ 对相邻的方格距离为 $3$，$2$ 对相邻的方格距离为 $5$。

  再如，对于 $2$ 阶皮亚诺曲线，距离和是 $816$。

  请求出对于 $12$ 阶皮亚诺曲线，距离和是多少。

  提示：答案不超过 $10^{18}$。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

184731576397539360

---

动态规划

---

  首先考虑分形问题，但是 $3^{12}\times 3^{12}$ 的曲线中，相邻的格子对有 $2\times 3^{12}\times (3^{12}-1)$ 个，复杂度爆炸。

  于是考虑动态规划，为此需要选择一些合适的属性来表述状态，合适的策略来完成转移。

  容易想到按阶划分，即将一个 $k$ 阶的皮亚诺曲线划分为 $3^3$ 个 $k-1$ 的皮亚诺曲线，而 $k-1$ 阶曲线内部相邻块的距离不受其余同阶曲线的影响，固有状态 $f_i$ 表示 $i$ 阶皮亚诺曲线的距离合，$f_i=3^3{f}_{i-1}+I_i$，$I_i$ 表示 $k-1$ 阶曲线直接相邻部分的距离合，而这正是下面要着重讨论的部分。

  对于 $2$ 阶皮亚诺曲线，它的 $1$ 阶曲线相邻的块有：

  容易发现，两行或两列之间相邻块的距离是相等的，于是只需讨论出一行一列的距离合的计算方法，将其和乘以 $2$ 即可计算出 $I_2$。

  其实到这一步问题已经得解，因为分形去求解两块之间的距离， $O(3^n)$ 的复杂度完全可以在短时间内计算出结果。

public class Test {
    
    

    public static void main(String[] args) {
    
      new Test().run(); }

    void run() {
    
    
        pow[1] = 1;
        for (int i = 2; i <= 13; i++) pow[i] = pow[i - 1] * 3;
        long f = 0, tmp;
        for (int i = 1; i <= 12; i++) {
    
    
            tmp = 0;
            for (int j = 0; j < pow[i + 1]; j++) {
    
    
                tmp += abs(calc(i, j, pow[i]) - calc(i, j, pow[i] - 1));
                tmp += abs(calc(i, pow[i], j) - calc(i, pow[i] - 1, j));
            }
            f = 9 * f + 2 * tmp;
        }
        System.out.println(f);
    }

    long[] pow = new long[14];

    long abs(long a) {
    
     return a > 0 ? a : -a; }

    long calc(int k, long x, long y) {
    
    
        if (k == 0) return 0;
        long offset = x /  pow[k] * 3;
        boolean flag = offset == 3;
        offset += flag ? (3 - y /  pow[k] - 1) : (y /  pow[k]);
        if ((offset & 1) == 1)
            x =  pow[k] - x %  pow[k] - 1;
        return flag ? ((offset + 1) * pow[k] * pow[k] - calc(k - 1, x %  pow[k], y %  pow[k]) - 1) :
                (offset *  pow[k] * pow[k] + calc(k - 1, x %  pow[k], y %  pow[k])) ;
    }
}

  有关分形问题可以看 $\mathrm{B}$、$\mathrm{C}$ 组皮亚诺曲线问题 的题解。

---

#E 玩具蛇

本题总分：$15$ 分

---

  小蓝有一条玩具蛇，一共有 $16$ 节，上面标着数字 $1$ 至 $16$。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
  小蓝还有一个 $4\times 4$ 的方格盒子，用于存放玩具蛇，盒子的方格上依次标着字母 $\mathrm{A}$ 到 $\mathrm{P}$ 共 $16$ 个字母。
  小蓝可以折叠自己的玩具蛇放到盒子里面。他发现，有很多种方案可以将玩具蛇放进去。
  下图给出了两种方案：

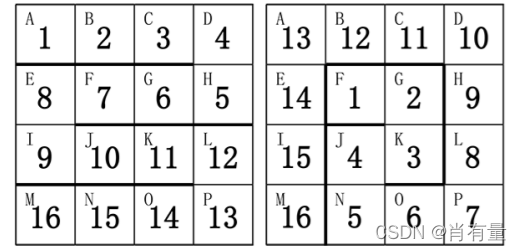
  请帮小蓝计算一下，总共有多少种不同的方案。如果两个方案中，存在玩具蛇的某一节放在了盒子的不同格子里，则认为是不同的方案。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

552

---

深度优先搜索

---

  模板题。

public class Test {
    
    

    public static void main(String[] args) {
    
      new Test().run(); }

    int N = 4, M = 4, ans = 0, target = N * M;

    int[][] offset = {
    
     {
    
    -1, 0}, {
    
    0, 1}, {
    
    1, 0}, {
    
    0, -1} };

    boolean[][] visited = new boolean[N + 2][M + 2];

    void run() {
    
    
        for (int i = 0; i <= N + 1; i++) visited[i][0] = visited[i][M + 1] = true;
        for (int i = 0; i <= M + 1; i++) visited[0][i] = visited[N + 1][i] = true;
        for (int i = 1; i <= N; i++)
            for (int j = 1; j <= M; j++) dfs(i, j, 1);
        System.out.println(ans);
    }

    void dfs(int x, int y, int depth) {
    
    
        visited[x][y] = true;
        if (depth == target) ans++;
        for (int i = 0, k, g; i < 4; i++) {
    
    
            k = x + offset[i][0];
            g = y + offset[i][1];
            if (!visited[k][g])
                dfs(k, g, depth + 1);
        }
        visited[x][y] = false;
    }
}

---

#F 游园安排

时间限制: $1.0\mathrm{s}$ 内存限制: $512.0\mathrm{M}\mathrm{B}$ 本题总分：$15$ 分

---

问题描述

  $\mathrm{L}$ 星球游乐园非常有趣，吸引着各个星球的游客前来游玩。小蓝是 $\mathrm{L}$ 星球游乐园的管理员。

  为了更好的管理游乐园，游乐园要求所有的游客提前预约，小蓝能看到系统上所有预约游客的名字。每个游客的名字由一个大写英文字母开始，后面跟 $0$ 个或多个小写英文字母。游客可能重名。

  小蓝特别喜欢递增的事物。今天，他决定在所有预约的游客中，选择一部分游客在上午游玩，其他的游客都在下午游玩，在上午游玩的游客要求按照预约的顺序排列后，名字是单调递增的，即排在前面的名字严格小于排在后面的名字。

  一个名字 $A$ 小于另一个名字 $B$ 是指：存在一个整数 $i$，使得 $A$ 的前 $i$ 个字母与 $B$ 的前 $i$ 个字母相同，且 $A$ 的第 $i+1$ 个字母小于 $B$ 的第 $i+1$ 个字母。（如果 $A$ 不存在第 $i+1$ 个字母且 $B$ 存在第 $i+1$ 个字母，也视为 $A$ 的第 $i+1$ 个字母小于 $B$ 的第 $i+1$ 个字母）

  作为小蓝的助手，你要按照小蓝的想法安排游客，同时你又希望上午有尽量多的游客游玩，请告诉小蓝让哪些游客上午游玩。如果方案有多种，请输出上午游玩的第一个游客名字最小的方案。如果此时还有多种方案，请输出第一个游客名字最小的前提下第二个游客名字最小的方案。如果仍然有多种，依此类推选择第三个、第四个…… 游客名字最小的方案。

---

输入格式

  输入包含一个字符串，按预约的顺序给出所有游客的名字，相邻的游客名 字之间没有字符分隔。

  其中有 ，每个名字的长度不超过 $10$ 个字母，输入的总长度不超过 $10^6$ 个字母。

---

输出格式

  按预约顺序输出上午游玩的游客名单，中间不加任何分隔字符。

---

测试样例₁

Input：
WoAiLanQiaoBei

Output：
AiLanQiao

---

评测用例规模与约定

  对于 $20$% 的评测数据，输入的总长度不超过 $20$ 个字母。
  对于 $50$% 的评测数据，输入的总长度不超过 $300$ 个字母。
  对于 $70$% 的评测数据，输入的总长度不超过 $10000$ 个字母。
  对于所有评测数据，每个名字的长度不超过 $10$ 个字母，输入的总长度不超过 $1000000$ 个字母。

---

最长单调子序列

---

  某种意义上也是道模板题，

  但题目额外增加了两个限制条件，方案打印和字典序最小，但原序列长度最长可达 $10^7$，这使得朴素的 $O(n^2)\mathrm{L}\mathrm{I}\mathrm{S}$ 排除在可选策略之内。

  于是考虑单调栈优化 $\mathrm{L}\mathrm{I}\mathrm{S}$，二分还原子序列打印方案，对于打印方案字典序最小，考虑倒序 $\mathrm{D}\mathrm{P}$，即倒着做一遍 $\mathrm{L}\mathrm{C}\mathrm{S}$，然后正着还原子序列，打印方案，

  实现细节什么的看代码吧。

import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Main {
    
    

    public static void main(String[] args) {
    
     new Main().run(); }

    void run() {
    
    
        StringBuilder builder = new StringBuilder();
        List<String> tourists = new ArrayList();
        for (int c = read(); c != -1; c = read()) {
    
    
            if (Character.isUpperCase(c) && builder.length() > 0) {
    
    
                tourists.add(builder.toString());
                builder.setLength(0);
            }
            builder.appendCodePoint(c);
        }
        if (builder.length() > 0)
            tourists.add(builder.toString());
        builder.setLength(0);
        List<String>[] answers = new List[tourists.size() + 1];
        List<Integer>[] idxs = new List[tourists.size() + 1];
        String[] stack = new String[tourists.size() + 1];
        Arrays.fill(stack, "");
        int top = 0;
        for (int i = tourists.size() - 1; i >= 0; i--) {
    
    
            int idx = 0, length = top;
            while (length > 0) {
    
    
                int half = length >> 1;
                if (tourists.get(i).compareTo(stack[idx + half]) >= 0) length = half;
                else {
    
    
                    length -= half - 1;
                    idx += half + 1;
                }
            }
            if (idx == top) top++;
            if (answers[idx] == null) {
    
    
                answers[idx] = new ArrayList();
                idxs[idx] = new ArrayList();
            }
            answers[idx].add(stack[idx] = tourists.get(i));
            idxs[idx].add(i);
        }
        String now = null, last = "";
        for (int i = top - 1, start = -1; i >= 0; i--, now = null) {
    
    
            for (int j = answers[i].size() - 1; j >= 0; j--) {
    
    
                if (idxs[i].get(j) > start && answers[i].get(j).compareTo(last) > 0 && (now == null || answers[i].get(j).compareTo(now) < 0)) {
    
    
                    now = answers[i].get(j);
                    start = idxs[i].get(j);
                }
            }
            builder.append(last = now);
        }
        System.out.println(builder);
    }

    byte[] buf = new byte[8192];

    int len, cur;

    int read() {
    
    
        if (cur >= len) {
    
    
            try {
    
    
                len = System.in.read(buf);
                cur = 0;
            } catch (IOException e) {
    
    
                e.printStackTrace();
            }
        }
        return len == -1 ? -1 : (buf[cur++] & 0xFF);
    }
}

  签到题这么搞挺恶心的，

  劝赛委组好自为之。

---

#G 画廊

时间限制: $1.0\mathrm{s}$ 内存限制: $512.0\mathrm{M}\mathrm{B}$ 本题总分：$20$ 分

---

问题描述

  小蓝办了一个画展，在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思，小蓝没有等距陈列自己的作品，而是按照更有艺术感的方式陈列。
  在画廊的左边陈列了 $L$ 幅作品，在画廊的右边陈列了 $R$ 幅作品，左边的作品距离画廊的起点依次为 $u_1,u_2,\cdots ,u_L$，右边的作品距离画廊起点依次为 $v_1,v_2,\cdots ,v_R$。
  每周，小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的，但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。
  小蓝从画廊的起点的正中央（左右两边的中点）出发，整理好每一幅画，最终到达画廊的终点的正中央。已知画廊的宽为 $w$。
  请问小蓝最少带着工具走多长的距离？

---

输入格式

  输入的第一行包含四个整数 $L,R,d,w$，表示画廊左边和右边的作品数量，以及画廊的长度和宽度。
  第二行包含 $L$ 个正整数 $u_1,u_2,\cdots ,u_L$，表示画廊左边的作品的位置。
  第三行包含 $R$ 个正整数 $v_1,v_2,\cdots ,v_R$，表示画廊右边的作品的位置。

---

输出格式

  输出一个实数，四舍五入保留两位小数，表示小蓝最少带着工具走的距离。

---

测试样例₁

Input：
3 3 10 2
1 3 8
2 4 6

Output：
14.71

Explanation：
小蓝从起点开始，首先到达左边第一幅作品（走动距离 √2），然后到达左
边第二幅作品（走动距离 2），然后到达右边第一幅作品（走动距离 √5），然后
到达右边第二幅和第三幅作品（走动距离 2 和 2），然后到达左边第三幅作品（走动距离 2√2），最后到达画廊终点（走动距离 √5）。
总共距离为 √2 + 2 + √5 + 2 + 2 + 2 √2 + √5 ≈ 14.71。

---

评测用例规模与约定

  对于 $40$% 的评测用例，$1\le L,R\le 10,1\le d\le 100,1\le w\le 100$。
  对于 $70$% 的评测用例，$1\le L,R\le 100,1\le d\le 1000,1\le w\le 1000$。
  对于所有评测用例，$1\le L,R\le 500,1\le d\le 100000,1\le w\le 100000,0\le u_1<u_2<\cdot \cdot \cdot <u_L\le d,0\le v_1<v_2<\cdot \cdot \cdot <v_R\le d$。

---

动态规划

---

  $\mathrm{T}\mathrm{S}\mathrm{P}$ 问题，具有 $\mathrm{N}\mathrm{P}$ 完全性，

  感兴趣的读者可以自行了解，

  总之设 $f_{l,r,0}$ 为小蓝当前在左边第 $l$ 幅画，此时已经整理了左边 $1\sim l$、右边 $1\sim r$ 幅画时所走的最短距离，$f_{l,r,1}$ 与 $f_{l,r,0}$ 意义大致相同，只不过在改状态小蓝最后在的位置为右边第 $r$ 辅画。

  因为无论哪种方案我们都不会再回到初始点，所以显然有初始值 $f_{i,0,0}=\sqrt{(\frac{w}{2}{)}^2+u_1^2}+u_i-u_1$、$f_{0,i,1}=\sqrt{(\frac{w}{2}{)}^2+v_1^2}+v_i-v_1$，其余为正无穷。

  答案为 $\min (f_{L,R,0}+\sqrt{(\frac{w}{2}{)}^2+(d-u_L{)}^2},f_{L,R,1}+\sqrt{(\frac{w}{2}{)}^2+(d-v_R{)}^2})$。

  转移方程为 $f_{l,r,0}=\min (f_{l-1,r,0}+w_i-w_{i-1},f_{l-1,r,1}+\sqrt{w^2+(v_r-w_l{)}^2})$，$f_{l,r,1}=\min (f_{l,r-1,0}+\sqrt{w^2+(v_r-w_l{)}^2}),f_{l,r-1,1}+v_r-v_{r-1})$。

import java.io.*;

import static java.lang.Math.hypot;
import static java.lang.Math.min;

public class Main {
    
    

    public static void main(String[] args) {
    
     new Main().run(); }

    void run() {
    
    
        InputReader in = new InputReader(System.in);
        int L = in.readInt(), R = in.readInt(), d = in.readInt();
        double w = in.readInt();
        int[] U = new int[L + 1];
        int[] V = new int[R + 1];
        for (int i = 1; i <= L; i++)
            U[i] = in.readInt();
        for (int i = 1; i <= R; i++)
            V[i] = in.readInt();
        double[][][] dp = new double[L + 1][R + 1][2];
        for (int i = 1; i <= L; i++) {
    
    
            dp[i][0][1] = Double.POSITIVE_INFINITY;
            dp[i][0][0] = hypot(w / 2, U[1]) + U[i] - U[1];
        }
        for (int i = 1; i <= R; i++) {
    
    
            dp[0][i][0] = Double.POSITIVE_INFINITY;
            dp[0][i][1] = hypot(w / 2, V[1]) + V[i] - V[1];
        }
        for (int l = 1; l <= L; l++)
            for (int r = 1; r <= R; r++) {
    
    
                dp[l][r][0] = min(dp[l - 1][r][0] + U[l] - U[l - 1], dp[l - 1][r][1] + hypot(w, V[r] - U[l]));
                dp[l][r][1] = min(dp[l][r - 1][0] + hypot(w, U[l] - V[r]), dp[l][r - 1][1] + V[r] - V[r - 1]);
            }
        System.out.printf("%.2f", min(dp[L][R][0] + hypot(w / 2, d - U[L]), dp[L][R][1] + hypot(w / 2, d - V[R])));
    }

    class InputReader {
    
    

        StreamTokenizer token;

        InputReader(InputStream in) {
    
    
            token = new StreamTokenizer(new BufferedReader(new InputStreamReader(in)));
        }

        int readInt() {
    
    
            try {
    
    
                token.nextToken();
            } catch (IOException e) {
    
    
                e.printStackTrace();
            }
            return (int)token.nval;
        }
    }
}

---

#H 奇偶覆盖

时间限制: $2.0\mathrm{s}$ 内存限制: $512.0\mathrm{M}\mathrm{B}$ 本题总分：$20$ 分

---

问题描述

  在平面内有一些矩形，它们的两条边都平行于坐标轴。

  我们称一个点被某个矩形覆盖，是指这个点在矩形的内部或者边界上。

  请问，被奇数个矩形覆盖和被偶数 $(\ge 2)$ 个矩形覆盖的点的面积分别是多少？

---

输入格式

  输入的第一行包含一个整数 $n$，表示矩形的个数。

  接下来 $n$ 行描述这些矩形，其中第 $i$ 行包含四个整数 $l_i,b_i,r_i,t_i$ ，表示矩形的两个对角坐标分别为 $(l_i,b_i),(r_i,t_i)$。

其中，$1\le n\le 10^5,0\le l_i<r_i\le 10^9,0\le b_i<t_i\le 10^9$ 。

---

输出格式

  输出两行。

  第一行包含一个整数，表示被奇数个矩形覆盖的点的面积。

  第二行包含一个整数，表示被偶数 $(\ge 2)$ 个矩形覆盖的点的面积。

---

测试样例₁

Input：
3
1 1 3 3
2 2 4 4
3 3 5 5

Output：
8
2

---

评测用例规模与约定

  对于 $20$% 的评测用例，$1\le n\le 10,0\le l_i<r_i\le 100,0\le b_i<t_i\le 100$。
  对于 $40$% 的评测用例，$1\le n\le 1000,0\le l_i<r_i\le 100,0\le b_i<t_i\le 100$。
  对于 $60$% 的评测用例，$1\le n\le 10000,0\le l_i<r_i\le 1000,0\le b_i<t_i\le 1000$。
  对于 $80$% 的评测用例，$1\le n\le 100000,0\le l_i<r_i\le 100000,0\le b_i<t_i\le 100000$。
  对于所有评测用例，$1\le n\le 100000,0\le l_i<r_i\le 10^9,0\le b_i<t_i\le 10^9$。

---

扫描线

---

  在扫描线的基础上加上奇数点个数查询就完了。

// 歇会再写

---

#I 补给

时间限制: $3.0\mathrm{s}$ 内存限制: $512.0\mathrm{M}\mathrm{B}$ 本题总分：$25$ 分

---

问题描述

  小蓝是一个直升飞机驾驶员，他负责给山区的 $n$ 个村庄运送物资。每个月，他都要到每个村庄至少一次，可以多于一次，将村庄需要的物资运送过去。每个村庄都正好有一个直升机场，每两个村庄之间的路程都正好是村庄之间的直线距离。
  由于直升机的油箱大小有限，小蓝单次飞行的距离不能超过 $D$。每个直升机场都有加油站，可以给直升机加满油。
  每个月，小蓝都是从总部出发，给各个村庄运送完物资后回到总部。如果方便，小蓝中途也可以经过总部来加油。
  总部位于编号为 $1$ 的村庄。
  请问，要完成一个月的任务，小蓝至少要飞行多长距离？

---

输入格式

  输入的第一行包含两个整数 $n$, $D$，分别表示村庄的数量和单次飞行的距离。
  接下来 n 行描述村庄的位置，其中第 $i$ 行两个整数 $x_i$, $y_i$，表示编号为 $i$ 的村庄的坐标。村庄 $i$ 和村庄 $j$ 之间的距离为 $\sqrt{(x_i-x_j{)}^2+(y_i-y_j{)}^2}$ 。

---

输出格式

  输出一行，包含一个实数，四舍五入保留正好 $2$ 位小数，表示答案。

---

测试样例₁

Input：
4 10
1 1
5 5
1 5
5 1

Output：
16.00

Explanation：
四个村庄形成一个正方形的形状。

测试样例₂

Input：
4 6
1 1
4 5
8 5
11 1

Output：
28.00

Explanation：
补给顺序为 1 → 2 → 3 → 4 → 3 → 2 → 1。

---

评测用例规模与约定

对于所有评测用例，$1\le n\le 20,1\le x_i,y_i\le 10^4,1\le D\le 10^5$。

---

// 挂着，还没写。

---

#J 蓝跳跳

时间限制: $10.0\mathrm{s}$ 内存限制: $512.0\mathrm{M}\mathrm{B}$ 本题总分：$25$ 分

---

问题描述

  小蓝制作了一个机器人，取名为蓝跳跳，因为这个机器人走路的时候基本靠跳跃。

  蓝跳跳可以跳着走，也可以掉头。蓝跳跳每步跳的距离都必须是整数，每步可以跳不超过 $k$ 的长度。由于蓝跳跳的平衡性设计得不太好，如果连续两次都是跳跃，而且两次跳跃的距离都至少是 $p$，则蓝跳跳会摔倒，这是小蓝不愿意看到的。

  小蓝接到一个特别的任务，要在一个长为 $L$ 舞台上展示蓝跳跳。小蓝要控制蓝跳跳从舞台的左边走到右边，然后掉头，然后从右边走到左边，然后掉头，然后再从左边走到右边，然后掉头，再从右边走到左边，然后掉头，如此往复。

  为了让观者不至于太无趣，小蓝决定让蓝跳跳每次用不同的方式来走。小蓝将蓝跳跳每一步跳的距离记录下来，按顺序排成一列，显然这一列数每个都不超过 $k$ 且和是 $L$。这样走一趟就会出来一列数。如果两列数的长度不同，或者两列数中存在一个位置数值不同，就认为是不同的方案。

  请问蓝跳跳在不摔倒的前提下，有多少种不同的方案从舞台一边走到另一边。

---

输入格式

  输入一行包含三个整数 $k,p,L$。

---

输出格式

  输出一个整数，表示答案。答案可能很大，请输出答案除以 $20201114$ 的余数。

---

测试样例₁

Input：
3 2 5

Output：
9

Explanation：
蓝跳跳有以下 9 种跳法：
1. 1+1+1+1+1
2. 1+1+1+2
3. 1+1+2+1
4. 1+2+1+1
5. 2+1+1+1
6. 2+1+2
7. 1+1+3
8. 1+3+1
9. 3+1+1

测试样例₂

Input：
5 3 10

Output：
397

---

评测用例规模与约定

  对于 $30$% 的评测用例，$1\le p\le k\le 50,1\le L\le 1000$。
  对于 $60$% 的评测用例，$1\le p\le k\le 50,1\le L\le 10^9$。
  对于 $80$% 的评测用例，$1\le p\le k\le 200,1\le L\le 10^{18}$。
  对于所有评测用例，$1\le p\le k\le 1000,1\le L\le 10^{18}$。

---

矩阵分块

---

  首先考虑动态规划，虽然问题的性质和数据规模使得我们很难确定一个合理的状态，找到一个合适的方法进行转移，

  但它山之石可以攻玉，不同知识之间若即若离的联系是不容小觑的。

  设 $F_i$ 表示舞台长为 $i$ 时，最后一步小于 $p$ 的方案数，$G_i$ 表示舞台长为 $i$ 时，最后一步不小于 $p$ 和 $k$ 的方案数，最后所求的答案即为 $F_L+G_L$。

  考虑 $F$、$G$ 的转移，有 $F_i={\sum }_{j=1}^{p-1}(F_{i-j}+G_{i-j})$、$G_i={\sum }_{j=p}^k{F}_{i-j}$，起初 $F_0=1$，复杂度为 $O(kL)$，难以通过半数用例，但个式子告诉我们，两个状态之间的转移是封闭的，这一点足够启发到我们使用矩阵快速幂来转移。

  对于 $k=3$、$p=2$、$L=5$ 的情况，将每次转移涉及到的向量最小表示为 $(F_i,G_i,F_{i-1},G_{i-1},F_{i-2},G_{i-2})$，根据状态转移方程可以列出状态转移矩阵，并可以将答案表示为：$$ans=c_{1,1}+c_{1,2},{\left(c_{i,j}\right)}_{2k\times 2k}={\left(\begin{array}{c}{F}_0\\ G_0\\ 0\\ 0\\ 0\\ 0\end{array}\right)}^{\mathrm{T}}{\left(\begin{array}{cccccc}1& 0& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 0\\ 0& 1& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right)}^L(\mathrm{m}\mathrm{o}\mathrm{d}20201114)$$

  可是矩阵乘法的复杂度在 $O(n^3)$，故整个算法复杂度为 $O(k^3\log L)$，还是不能接受，而且这个矩阵很难拆分出可交换矩阵使用广义二项式定理做累加的计算，总之考虑矩阵分块。

  设 $A=\left(\begin{array}{cc}1& 0\\ 1& 0\end{array}\right)$、$B=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)$，则对于任意 $k$，$p$ 的转移矩阵都可以表示为$$\left(\begin{array}{cccccc}A& E& O& O& O& O\\ ⋮& O& E& O& O& O\\ A& O& O& E& O& ⋮\\ B& ⋮& \ddots & \cdots & O& O\\ ⋮& ⋮& O& O& E& O\\ B& O& O& O& O& O\end{array}\right)$$

  好像有点问题，歇会，明天写。

// 挂着，还没写。

---