一、正交和平行透视法

现在我们知道如何表示2D和3D几何图元以及如何在空间上转换它们，我们需要指定如何将 3D图元投影到图像平面上。我们可以使用线性3D到2D投影矩阵来做到这一点。最简单的模型是正交法，它不需要除法就可以得到最终的（不均匀的）结果。更常用的模型是透视，因为它更准确地模拟了真实相机的行为。

正交投影只是简单地丢弃三维坐标 $p$ 的 $z$ 分量以获得 2D 点 $x$ 。（在这里使用 $p$ 表示 3D 点，使用 $x$ 表示 2D 点。）这可以写成 $x = \left [ I_{2\times 2} \right | 0] P$ ，如果我们使用齐次（投影）坐标，我们可以写 $\tilde{x} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \tilde{P}$ ，即，我们删除 $z$ 分量但保留 $w$ 分量。正交法是长焦（望远）镜头和深度相对于相机距离较浅的物体的近似模型。它仅适用于远心镜头。

远心镜头（Telecentric），主要是为纠正传统工业镜头视差而设计，它可以在一定的物距范围内，使得到的图像放大倍率不会变化，这对被测物不在同一物面上的情况是非常重要的应用。远心镜头由于其特有的平行光路设计一直为对镜头畸变要求很高的机器视觉应用场合所青睐。

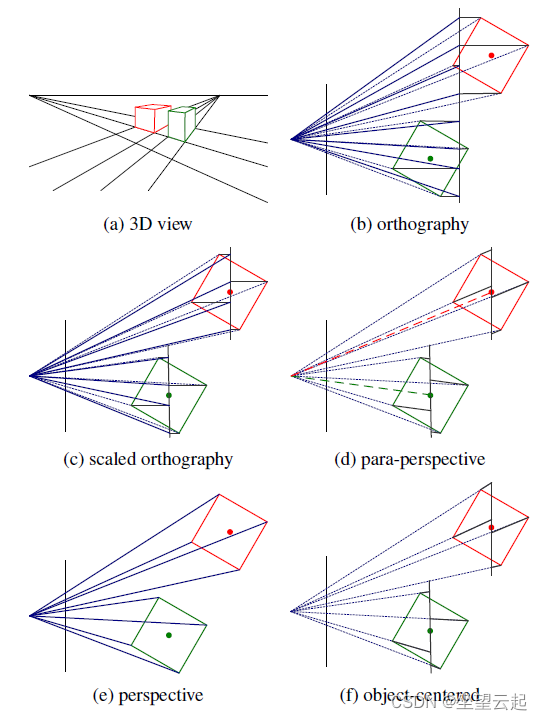
图1：常用投影模型：(a) 3D 世界视图，(b) 正字法，(c) 缩放正字法，(d) 平行透视，(e) 透视，(f) 以对象为中心。每个图表都显示了投影的俯视图。注意地平面和盒子侧面的平行线在非透视投影中是如何保持平行的。

在实践中，世界坐标（可能以米为单位测量尺寸）需要缩放以适合图像传感器（物理上以毫米为单位测量，但最终以像素为单位测量）。正因如此，缩放正交其实更常用， $x = \left [ sI_{2\times 2} \right | 0] P$ 该模型等价于首先将世界点投影到局部正面平行图像平面上，然后使用常规透视投影缩放该图像。对于场景的所有部分，缩放比例可以相同（图1b），也可以对于独立建模的对象不同（图1c）。更重要的是，当从运动估计结构时，缩放可以因帧而异，这可以更好地模拟物体接近相机时发生的缩放变化。

缩放正交是一种流行的模型，用于重建远离相机的物体的3D形状，因为它极大地简化了某些计算。例如，可以使用简单的最小二乘法估计姿势（相机方向）。在正交下，可以使用分解（奇异值分解）同时估计结构和运动。

一个密切相关的投影模型是平行透视。在该模型中，对象点再次首先投影到平行于图像平面的局部参考上。然而，它们不是垂直投影到该平面，而是平行于视线投影到物体中心（图1d）。接下来是通常投影到最终图像平面上，这又相当于一个缩放。因此这两个投影的组合是仿射的，可以写成 $\tilde{x} = \begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13}\\ 0 & 0 & 0 & 1 \end{bmatrix} \tilde{P}$ 。

请注意3D中的平行线在图1b-d 中投影后如何保持平行。与缩放正交法相比，准透视法提供了更准确的投影模型，而不会增加按像素透视分割的复杂性，这会使传统的分解方法无效。

二、透视法

计算机图形学和计算机视觉中最常用的投影是真正的 3D 透视图（图1e）。在这里，点通过将它们除以它们的 $z$ 分量来投影到图像平面上。使用非齐次坐标，这可以写成

在齐次坐标中，投影具有简单的线性形式，

即，我们删除 $p$ 的 $w$ 分量。

在计算机图形系统中常见的一种形式是两步投影，首先将 3D 坐标投影到标准化设备坐标 $(x, y, z) \in \left [ -1, 1 \right ] \times \left [ -1, 1 \right ] \times \left [ 0, 1 \right ]$ ，然后使用viewport变换将这些坐标重新缩放为整数像素坐标。然后使用 $4\times 4$ 矩阵表示（初始）透视投影

$\tilde{x} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -z_{far}/z_{range} & z_{near}z_{far}/z_{range}\\ 0 & 0 & 1 & 0 \end{bmatrix}$

其中 $z_{near}$ 和 $z_{far}$ 是近和远 $z$ 剪裁平面， $z_{range} = z_{far} - z_{near}$ 。请注意，前两行实际上是按焦距和纵横比缩放的，因此可见光线映射到 $(x, y, z) \in \left [ -1, 1 \right ]^2$ 。保留第三行而不是删除它的原因是可见性操作（例如 $z$ 缓冲）需要渲染的每个图形元素的深度。

如果我们设置 $z_{near} = 1$ ， $z_{far}\rightarrow \infty$ ，并切换第三行的符号，归一化的屏幕矢量的第三个元素变为反深度，即视差。在许多情况下，这非常方便，因为对于在户外移动的相机，相机的逆深度通常是比直接 3D 距离更好的参数化。

虽然常规的2D图像传感器无法测量到表面点的距离，但距离传感器和立体匹配算法可以计算这些值。然后，能够使用 $4 \times 4$ 矩阵的逆矩阵将基于传感器的深度或视差值 $d$ 直接映射回3D 位置是很方便的。如果我们使用全秩 $4\times 4$ 矩阵表示透视投影，可以做到这一点。

三、相机内在函数

一旦我们使用投影矩阵通过理想的针孔投影了 3D 点，我们仍然必须根据像素传感器间距和传感器平面与原点的相对位置来转换结果坐标。下图显示了所涉及的几何图形。首先使用传感器单应性 $M_s$ 呈现从 2D 像素坐标到 3D 射线的映射，因为这更容易用物理可测量的量来解释。然后，我们将这些量与更常用的相机内在矩阵 $K$ 相关联，该矩阵用于将 3D 相机中心点 $p_c$ 映射到 2D 像素坐标 $\tilde{x}_s$ 。

图像传感器返回由整数像素坐标 $(x_s, y_s)$ 索引的像素值，通常坐标从图像的左上角开始向下和向右移动。（并非所有成像库都遵守此约定，但其他坐标系的调整很简单。）为了将像素中心映射到3D坐标，我们首先通过像素间距 $(s_x, s_y)$ 缩放 $(x_s, y_s)$ 值（有时表示以微米为单位的固态传感器），然后用原点 $c_s$ 和 3D 旋转 $R_s$ 描述传感器阵列相对于相机投影中心 $O_c$ 的方向（上图）。

然后组合的 2D 到 3D 投影可以写为, $3 \times 3$ 矩阵M的前两列是图像像素阵列中沿 $x_s$ 和 $y_s$ 方向的单位步长对应的3D向量，而第三列是3D图像阵列原点 $c_s$ 。

矩阵 $M_s$ 由八个未知数参数化：描述旋转 $R_s$ 的三个参数、描述平移 $c_s$ 的三个参数和两个比例因子 $(s_x, s_y)$ 。请注意，我们在这里忽略了图像平面上两个轴之间偏斜的可能性，因为固态制造技术可以忽略不计。在实践中，除非我们对传感器间距或传感器方向有准确的外部知识，否则只有七个自由度，因为仅基于外部图像测量，无法将传感器与原点的距离与传感器间距分开。

然而，估计具有所需七个自由度的相机模型 $M_s$ （即，前两列在适当的重新缩放后正交）是不切实际的，因此大多数从业者假设一般的 $3 \times 3$ 齐次矩阵形式。

3D 像素中心 $p$ 和 3D 相机中心点 $p_c$ 之间的关系由未知缩放 $s$ 给出， $p = sp_c$ 。因此，我们可以将 $p_c$ 和像素地址 $\tilde{x}_s$ 的同质版本之间的完整投影写为 $3 \times 3$ 矩阵 K 被称为校准矩阵，它描述了相机的内在特性（与相机在空间中的方向相反，称为外在特性）。

从上面的讨论中，我们看到K理论上有7个自由度，实际上有8个自由度（ $3 \times 3$ 齐次矩阵的全维）。那么，为什么大多数关于 3D 计算机视觉和多视图几何的教科书都将 K 视为具有五个自由度的上三角矩阵？

虽然这在这些书中通常没有明确说明，但这是因为我们无法仅基于外部测量来恢复完整的 K 矩阵。当基于外部3D点或其他测量值校准相机时，我们最终会使用一系列测量值同时估计内在 $(K)$ 和外在 $(R, t)$ 相机参数，其中 $p_w$ 是已知的 3D 世界坐标，称为相机矩阵。 $P=K[R | t]$ 。检查这个方程，我们可以看到我们可以将 $K$ 后乘以 $R_1$ 并将 $[R | t]$ 预乘以 $R^T_1$ ，并且仍然可以得到有效的校准。因此，仅基于图像测量来了解传感器的真实方向和真实的相机内在特性是不可能的。

$K$ 的上三角形式的选择似乎是常规的。给定一个完整的 $3 \times 4$ 相机矩阵 $P=K[R | t]$ ，我们可以使用 QR 分解计算上三角 K 矩阵。（注意术语的冲突：有的代数教材中，R 表示上三角（对角线右侧）矩阵；在计算机视觉中，R 是正交旋转。）

有几种方法可以写出 K 的上三角形式。一种可能是它对传感器 x 和 y 尺寸使用独立的焦距 $f_x$ 和 $f_y$ 。由于传感器没有垂直于光轴安装，这些条目对传感器轴之间任何可能的偏斜进行编码，并且 $(c_x, c_y)$ 表示以像素坐标表示的图像中心。图像中心在计算机视觉文献中也经常被称为主点，尽管在光学中，主点是通常位于镜头内部的 3D 点，其中主平面与主（光）轴相交。

另一种可能是其中纵横比 a 已明确，并使用共同的焦距 f。

在实践中，对于许多应用程序，可以通过设置 a = 1 和 s = 0 来获得更简单的形式，通常，将原点设置在图像的大致中心，例如 $(c_x, c_y) = (W/2, H/2)$ ，其中 W 和 H 分别是图像的宽度和高度，可以得到一个完美可用的相机具有单个未知数的模型，即焦距 f。

（图）显示焦距 $f$ 和图像中心 $(c_x, c_y)$ 的简化相机内在函数。图像宽度和高度分别为 W 和 H。

上图显示了如何将这些量可视化为简化成像模型的一部分。请注意，现在我们已将图像平面放置在节点（镜头的投影中心）的前面。 y 轴的意义也被翻转以获得与大多数成像库处理垂直（行）坐标的方式兼容的坐标系。

四、关于焦距

如何表示焦距的问题是在实现计算机视觉算法和讨论其结果时经常引起混淆的问题。这是因为焦距取决于用于测量像素的单位。

如果我们使用整数值对像素坐标进行编号，例如 [0，W) [0，H)，则中的焦距 f 和相机中心 $(c_x, c_y)$ 可以表示为像素值。这些数量与摄影师使用的更熟悉的焦距有何关系？

下图说明了焦距 f、传感器宽度 W 和水平视场 H 之间的关系，它们遵循下面公式

对于传统的 35mm 胶片相机，其有效曝光区域为 24mm×36mm，我们有 W = 36mm ，因此 $f$ 也以毫米表示。例如，单反（单反）相机通常配备的“备用”镜头为 50mm，这是一个很好的长度，而 85mm 是人像的标准摄影。然而，由于我们使用数字图像，以像素表示 W 更方便，因此焦距 f 可以直接用于校准矩阵 K。

另一种可能性是缩放像素坐标，使它们从 $[1, -1)$ 沿着较长的图像维度和 $[-a^{-1}, a^{-1})$ 沿短轴，其中 $a \geq 1$ 是图像纵横比（与前面介绍的传感器单元纵横比相反）。这可以使用修改后的归一化设备坐标来完成，

这样做的好处是焦距 f 和图像中心 $(c_x, c_y)$ 与图像分辨率无关，这在使用多分辨率图像处理算法（如图像金字塔）时很有用。使用 $S$ 代替 $W$ 也使得风景（水平）和肖像（垂直）照片的焦距相同，就像 35mm 摄影中的情况一样。（在一些计算机图形学教科书和系统中，标准化的设备坐标从 $[-1, 1] \times [-1, 1]$ 开始，使用两个不同的焦距来描述相机的内在特性）设置 $S = W = 2$ ，我们得到更简单（无单位）的关系