图神经网络（二）GCN的性质（3）GCN是一个低通滤波器

 在图的半监督学习任务中，通常会在相应的损失函数里面增加一个正则项，该正则项需要保证相邻节点之间的类别信息趋于一致，一般情况下，我们选用拉普拉斯矩阵的二次型作为正则约束：
$$L=L_0+L_{\text{reg}},L_{\text{reg}}=\sum _{e_{ij}\in E}{A}_{ij}\Vert f(x_i)-f(x_j){\Vert }^2=f(X{)}^{\text{T}}Lf(x)$$
 其中$L$表示模型的总损失，$L_0$表示监督损失，$L_{\text{reg}}$表示正则项，从学习的目标来看，这样的正则项使得相邻节点的分类标签尽量一致，这种物以类聚的先验知识，可以指导我们更加高效地对未标记的数据进行学习。从图信号的角度来看，我们知道该正则项也表示图信号的总变差，减小该项表示我们期望经过模型之后的图信号更加平滑，根据前面所学的知识，从频域上来看，相当于对图信号做了低通滤波的处理[6]。

 在GCN的损失函数中，我们通常并不会设计这样的正则项。但是有研究表明，论文[4]中将GCN视为一种低通滤波器，下面阐述具体的过程：

 回到GCN的核心计算式${\tilde{L}}_{\text{sym}}XW$上，体现图滤波的方法就在于左乘了一个重归一化形式的拉普拉斯矩阵${\tilde{L}}_{\text{sym}}XW$，根据上一章的相关内容可知，要确定是否为低通滤波，我们就必须去研究${\tilde{L}}_{\text{sym}}XW$对应的频率响应函数$p(\lambda )$的性质。
$$\begin{array}{rl}{\tilde{L}}_{\text{sym}}& ={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}\\ & ={\tilde{D}}^{-1/2}(\tilde{D}-L){\tilde{D}}^{-1/2}\\ & =I-{\tilde{D}}^{-1/2}L{\tilde{D}}^{-1/2}\\ & =I-{\tilde{L}}_s\end{array}$$
 由于${\tilde{L}}_s$可以被正交对角化，我们设${\tilde{L}}_s=V\tilde{\Lambda }{V}^{\text{T}}$，${\tilde{\lambda }}_i$是${\tilde{L}}_s$的特征值，可以证明${\tilde{\lambda }}_i\in [0,2)$[5]。

 因此上式变为：
$${\tilde{L}}_{\text{sym}}=I-V\tilde{\Lambda }{V}^T=V(1-\tilde{\Lambda })V^{\text{T}}$$
 显然，其频率响应函数为$p(\lambda )=1-{\tilde{\lambda }}_i\in [-1,1)$，该函数是一个线性收缩的函数，因此能起到对图信号进行低通滤波的作用。

 如果将信号矩阵$X$不断左乘$K$次${\tilde{L}}_{\text{sym}}$，则对应频率响应函数为$(1-{\tilde{\lambda }}_i{)}^K$，图2-9所示为该函数的图像：

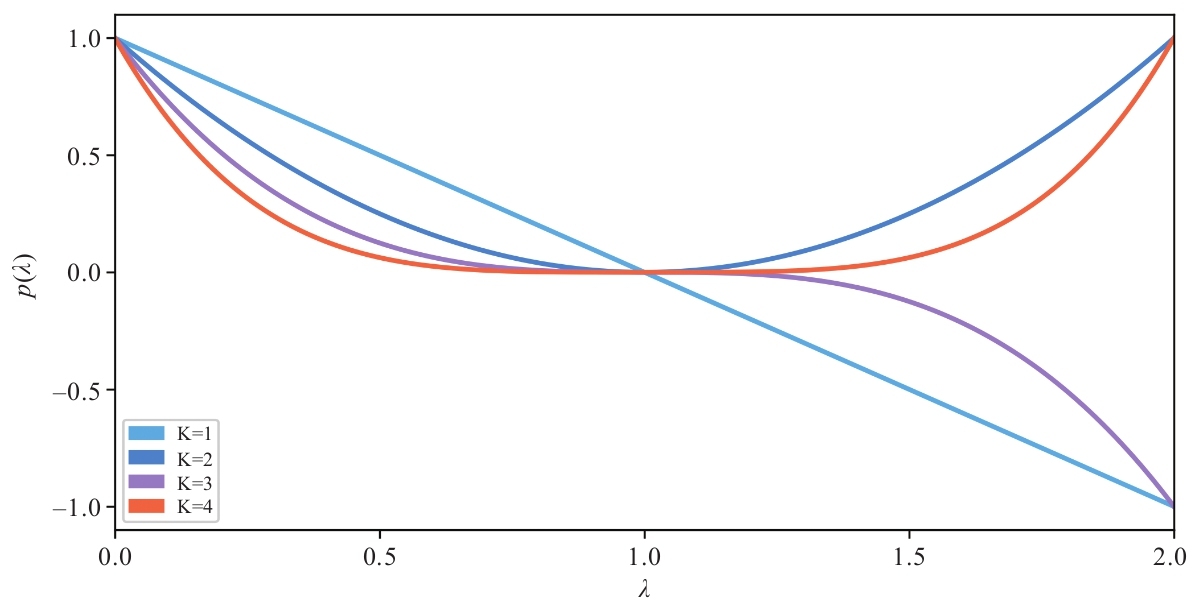图2-9 响应函数图像

 从图中可以看到，随着$K$的增大，频率响应函数在低频段上有着更强的缩放效果，因此是一种更强效应的低通滤波器。这种堆叠式的滤波操作，在一定程度上解释了多层GCN模型对于信号的平滑能力。事实上，为了更好地突出这种能力、较少模型的参数量，在论文[1] [2] [6]中直接将多层GCN退化成 $\sigma ({\tilde{L}}_{\text{sym}}^{K}XW)$。

 为什么要突出对数据的低通滤波呢？或者说，多层GCN的这种滤波效果对于图数据的任务学习会更加高效吗？在论文[3]中，作者论证了一个关于图数据的假设——输入数据的特征信号包括低频信号与高频信号，低频信号包含着对任务学习更加有效的信息。

 为此，作者Cora、Citeseer、Pubmed数据集上做了实验，这3个数据集都是论文引用网络。节点是论文，边是论文之间的引用关系。作者设计了一个实验，通过低通滤波截掉数据中的高频信息，然后使用剩下的低频信息进行分类学习，具体过程如下：

 （1）对数据集的${\tilde{L}}_s$进行正交对角化，得到傅里叶基$V$。

 （2）对输入的信号矩阵增加高斯噪声$X\leftarrow X+N(0,{\sigma }^2)$，其中$\sigma (0,0.01,0.05)$。

 （3）计算输入的信号矩阵在前k个最小频率上的傅里叶变换系数${\tilde{X}}_k=V[:,:k{]}^{\text{T}}{\tilde{D}}^{-1/2}X$。

 （4）利用逆傅里叶变换重构信号$X_k={\tilde{D}}^{-1/2}V[:,:k]{\tilde{X}}_k$。

 （5）将重构后的信号送到一个两层的MLP网络进行分类学习，并记录准确率。

 图2-10所示为重构信号用的频率分量的比例（前$k$个最小频率占总频率数的比例）与分类准确率之间的关系图。作为对比实验，使用完整的原始信号矩阵在gfNN模型（论文[4]中的一种GCN的变体模型）与双层MLP上的分类准确率（3组图中的上部gfNN与中部MLP水平虚线）来进行对比。从该图中可以看出，在3个数据集上，最高的分类准确率集中在仅用最小的前20%的频段恢复信号的实验中，增加高频信息参与信号重构，模型的分类效果会下降。同时，增加高斯噪声会造成分类准确率下降，这种效应随着重构所用的频率分量的比例的增加而增强，这说明了使用低通滤波对数据进行去噪的有效性。作为对比实验，我们可以看到，即使在原始的输入数据上，gfNN也能取得所有实验中的最好效果，这说明gfNN本身就具有低通滤波的作用。

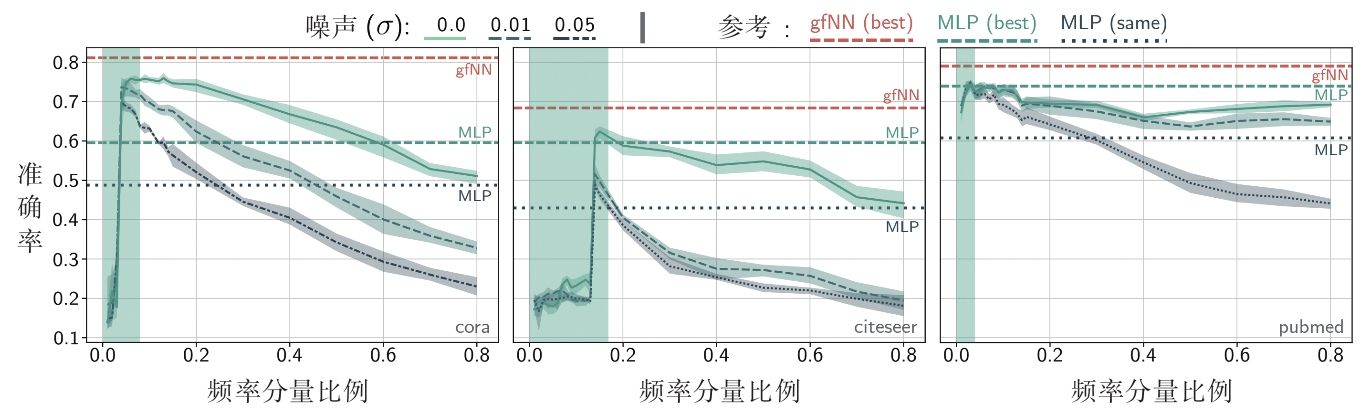图2-10 实验结果[5]

 从本节的介绍中可以看到，从频域去理解图数据以及GCN都具有十分重要的价值。对数据有效频率成分的分析可以指导我们发现数据的内在规律，从而更好地设计符合特定需求的滤波器，让GCN对于任务的高效学习做到有的放矢。

参考文献

[1] Maehara T.Revisiting Graph Neural Networks ： All We Have is Low-Pass Filters[J].arXiv preprint arXiv ： 1905.09550 ， 2019.

[2] Wu F ， Zhang T ， Souza Jr A H ， et al.Simplifying graph convolutional networks[J].arXiv preprint arXiv ： 1902.07153 ， 2019.

[3] Maehara T.Revisiting Graph Neural Networks ： All We Have is Low-Pass Filters[J].arXiv preprint arXiv ： 1905.09550 ， 2019.

[4] Maehara T.Revisiting Graph Neural Networks ： All We Have is Low-Pass Filters[J].arXiv preprint arXiv ： 1905.09550 ， 2019.

[5] Maehara T.Revisiting Graph Neural Networks ： All We Have is Low-Pass Filters[J].arXiv preprint arXiv ： 1905.09550 ， 2019.

[6] 刘忠雨, 李彦霖, 周洋.《深入浅出图神经网络: GNN原理解析》.机械工业出版社.