目录
1. 图网络的分类
在最开始,我们先梳理一下经常被提到的几个术语的区别和联系,也就是Graph Embedding,Graph Neural Network和Graph Convolutional Network的区别和联系是什么。
- Graph Embedding
图嵌入(Graph Embedding/Network Embedding,GE),属于表示学习的范畴,也可以叫做网络嵌入,图表示学习,网络表示学习等等。通常有两个层次的含义
1)将图中的节点表示成低维、实值、稠密的向量形式 ,使得得到的向量形式可以在向量空间中具有表示以及推理的能力,这样的向量可以用于下游的具体任务中。例如用户社交网络得到节点表示就是每个用户的表示向量,再用于节点分类等;
2)将整个图表示成低维、实值、稠密的向量形式 ,用来对整个图结构进行分类;
图嵌入的方式主要有三种:
1)矩阵分解: 基于矩阵分解的方法是将节点间的关系用矩阵的形式加以表达,然后分解该矩阵以得到嵌入向量。通常用于表示节点关系的矩阵包括邻接矩阵,拉普拉斯矩阵,节点转移概率矩阵,节点属性矩阵等。根据矩阵性质的不同适用于不同的分解策略。
2)DeepWalk 是基于 word2vec 词向量提出来的。word2vec 在训练词向量时,将语料作为输入数据,而图嵌入输入的是整张图,两者看似没有任何关联。但是 DeepWalk 的作者发现,语料中词语出现的次数与在图上随机游走节点被访问到的次数都服从幂律分布。因此 DeepWalk 把节点当做单词,把随机游走得到的节点序列当做句子,然后将其直接作为 word2vec 的输入可以得到节点的嵌入表示,同时利用节点的嵌入表示作为下游任务的初始化参数可以很好的优化下游任务的效果,也催生了很多相关的工作;
3)Graph Neural Network: 图结合deep learning方法搭建的网络统称为图神经网络GNN,也就是下一小节的主要内容,因此图神经网络GNN可以应用于图嵌入来得到图或图节点的向量表示;
- Graph Neural Network
图神经网络(Graph Neural Network, GNN)是指神经网络在图上应用的模型的统称,根据采用的技术不同和分类方法的不同,又可以分为下图中的不同种类,例如从传播的方式来看,图神经网络可以分为图卷积神经网络(GCN),图注意力网络(GAT,缩写为了跟GAN区分),Graph LSTM等等,本质上还是把文本图像的那一套网络结构技巧借鉴过来做了新的尝试。但在这篇文章中并不会细细介绍下面的每一种,作为入门篇,我们着重理解最经典和最有意义的基础模型GCN,这也是理解其他模型的基础。

图神经网络GNN的分类:分别从图的类型,训练的方式,传播的方式三个方面来对现有的图模型工作进行划分。
- Graph Convolutional Network
图卷积神经网络(Graph Convolutional Network, GCN)正如上面被分类的一样,是一类采用图卷积的神经网络,发展到现在已经有基于最简单的图卷积改进的无数版本,在图网络领域的地位正如同卷积操作在图像处理里的地位。

如上图所示,这三个比较绕的概念可以用一句话来概括:图卷积神经网络GCN属于图神经网络GNN的一类,是采用卷积操作的图神经网络,可以应用于图嵌入GE。
2. 卷积
要理解图卷积网络的核心操作图卷积,可以类比卷积在CNN的地位。
如下图所示,数字图像是一个二维的离散信号,对数字图像做卷积操作其实就是利用卷积核(卷积模板)在图像上滑动,将图像点上的像素灰度值与对应的卷积核上的数值相乘,然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值,并最终滑动完所有图像的过程。
用随机的共享的卷积核得到像素点的加权和从而提取到某种特定的特征,然后用反向传播来优化卷积核参数,就可以自动的提取特征,是CNN特征提取的基石 。

然而,现实中 更多重要的数据集都是用图的形式存储的,例如社交网络信息,知识图谱,蛋白质网络,万维网等等。这些图网络的形式并不像图像,是排列整齐的矩阵形式,而是非结构化的信息,那有没有类似图像领域的卷积一样,有一个通用的范式来进行图特征的抽取呢 ?这就是图卷积在图卷积网络中的意义。
对于大多数图模型,有一种类似通式的存在,这些模型统称GCNs。因此可以说,图卷积是处理非结构化数据的大利器,随着这方面研究的逐步深入,人类对知识领域的处理必将不再局限于结构化数据( CV,NLP),会有更多的目光转向这一存在范围更加广泛,涵盖意义更为丰富的知识领域。
接下来我们就来逐步拆解这个范式。
3. 图卷积

- 图定义
对于图,我们有以下特征定义:
对于图,V是节点的集合,E为边的集合,对于图中的每个节点i(i=1,...,N),均有其对应的特征(向量)
,整个图可以用矩阵
表示。其中N表示图中的节点数,D表示每个节点的特征数,即特征向量的维度。
- 图卷积的形象化理解
在一头扎进图卷积公式之前,我们先从其他的角度理解一下这个操作的物理含义,有一个形象化的理解,我们在试图得到节点表示的时候,容易想到的最方便有效的手段就是利用它周围的节点,也就是它的邻居节点或者邻居的邻居等等,这种思想可以归结为一句话:
图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡,关系越亲近的邻居影响越大。
实际上从邻居节点获取信息的思想在很多领域都有应用,例如word2vec,例如pagerank。关于这个点展开的内容文章[2]有非常详细的解释。
更加细节的如何从傅立叶变换到拉普拉斯算子到拉普拉斯矩阵的数学推导可以转向博客[7],为了避免数学功底没有那么强的初学者(比如我)被绕晕,我们先建立大纲,不要太发散。
- 图相关矩阵的定义
那么有什么东西来度量节点的邻居节点这个关系呢,学过图论的就会自然而然的想到邻接矩阵和拉普拉斯矩阵。举个简单的例子,对于下图中的左图(为了简单起见,举了无向图且边没有权重的例子(也可以认为权重为1))而言,它的度矩阵D,邻接矩阵 A和拉普拉斯矩阵L分别如下图所示,度矩阵D只有对角线上有值,为对应节点的度,其余为0;邻接矩阵A只有在有边连接的两个节点之间为1(如果是有权图,值为两个节点之间的权重),其余地方为0;拉普拉斯矩阵L为D-A。但需要注意的是,这是最简单的一种拉普拉斯矩阵,除了这种定义,还有接下来介绍的几种拉普拉斯矩阵。

4. 图卷积的通式
任何一个图卷积层都可以写成这样一个非线性函数:
为第一层的输入,
,N为图中节点的个数,D为每个节点特征向量的维度,A为邻接矩阵,不同模型的差异点在于函数f的实现不同。
下面介绍几种具体的实现,但是每一种实现的参数大家都统称拉普拉斯矩阵。
- 实现一
其中为第l层的权重参数矩阵,
为非线性激活函数,例如ReLU。
这种思路是基于节点特征与其所有邻居节点有关的思想。邻接矩阵A与特征H相乘,等价于,某节点的所有邻居节点(有边相连)的特征相加。这样多层隐含层叠加,能利用多层邻居的信息。
但这样存在两个问题:
1)没有考虑节点自身对自己的影响;
2)邻接矩阵A没有被规范化,这在提取图特征时可能存在问题,比如邻居节点多的节点倾向于有更大的影响力。
因此实现二和实现三针对这两点进行了优化。
- 实现二
拉普拉斯矩阵L=D-A,学名Combinatorial Laplacian,是针对实现一的问题1的改进
引入了度矩阵,从而解决了没有考虑自身节点信息自传递的问题
- 实现三
对于这里的拉普拉斯矩阵,学名Symmetric normalized Laplacian,也有论文或者博客写
,就是一个符号的差别,但本质上还是实现一的两个问题进行的改进:
1)引入自身度矩阵,解决自传递问题;
2)对邻接矩阵的归一化操作,通过对邻接矩阵两边乘以节点的度开方然后取逆得到。 具体到每一个节点对 i,j,矩阵中的元素由下面的式子给出(对于无向无权图):

其中分别表示节点i,j的度,也就是度矩阵在节点i,j处((i,i)(j,j))的值。
可能有一点比较疑惑的是怎么两边乘以一个矩阵的逆就归一化了? 这里需要复习到矩阵取逆的本质是做什么。
我们回顾下矩阵的逆的定义,对于式子,假如我们希望求矩阵X,那么当然是令等式两边都乘以
,然后式子就变成了
.
举个例子对于,单个节点运算来说,做归一化就是除以它节点的度,这样每一条邻接边信息传递的值就被规范化了,不会因为某一个节点有10条边而另一个只有1条边导致前者的影响力比后者大,因为做完归一化前者(每条边)的权重只有0.1了,从单个节点上升到二维矩阵的运算,就是对矩阵求逆了,乘以矩阵的逆的本质,就是做矩阵除法完成归一化。但左右分别乘以节点i,j度的开方,就是考虑一条边的两边的点的度。
常见的拉普拉斯矩阵除了以上举的两种,还有等等[3][4],归一化的方式有差别,根据论文[5]的实验,这些卷积核的形式并没有一种能够在任何场景下比其他的形式效果好,因此在具体使用的时候可以进行多种尝试,但主流的还是实现三,也就是大多数博客提到的。
- 另一种表述
上面是以矩阵的形式计算,可能会看起来非常让人疑惑,下面从单个节点的角度来重新看下这些个公式(本质是一样的,上文解释过,对于单个节点就是除法,对于矩阵就是乘以度矩阵的逆),对于第l+1层的节点的特征,对于它的邻接节点
,N是节点i的所有邻居节点的集合,可以通过以下公式计算得到:
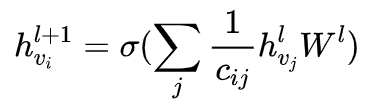
其中,,
,
为i的邻居节点的集合,
为i,j的度,这跟上面的公式其实是等价的,所以有些地方的公式是这个,有些是上面那个。
5. 参考文献
[1] https:// zhuanlan.zhihu.com/p/77729049 图嵌入的分类
[2] https://www.zhihu.com/question/54504471/answer/630639025 关于图卷积的物理学解释
[3] https://www.zhihu.com/question/54504471/answer/332657604拉普拉斯公式推倒细节,包括谱分解和傅立叶变换
[4] http://tkipf.github.io/graph-convolutional-networks 两篇论文细讲
[5] https://github.com/conferencesub/ICLR_2020各种图卷积核比较
[6] https://persagen.com/files/misc/scarselli2009graph.pdfGNN首次被提出的paper
[7] https://zhuanlan.zhihu.com/p/85287578 拉普拉斯矩阵和拉普拉斯算子的关系
