有向图的强连通分量
1.强连通 代表的是 这个连通块中的每两个点互相都是有一条路径是可以走到的
2.分量 就是子图;
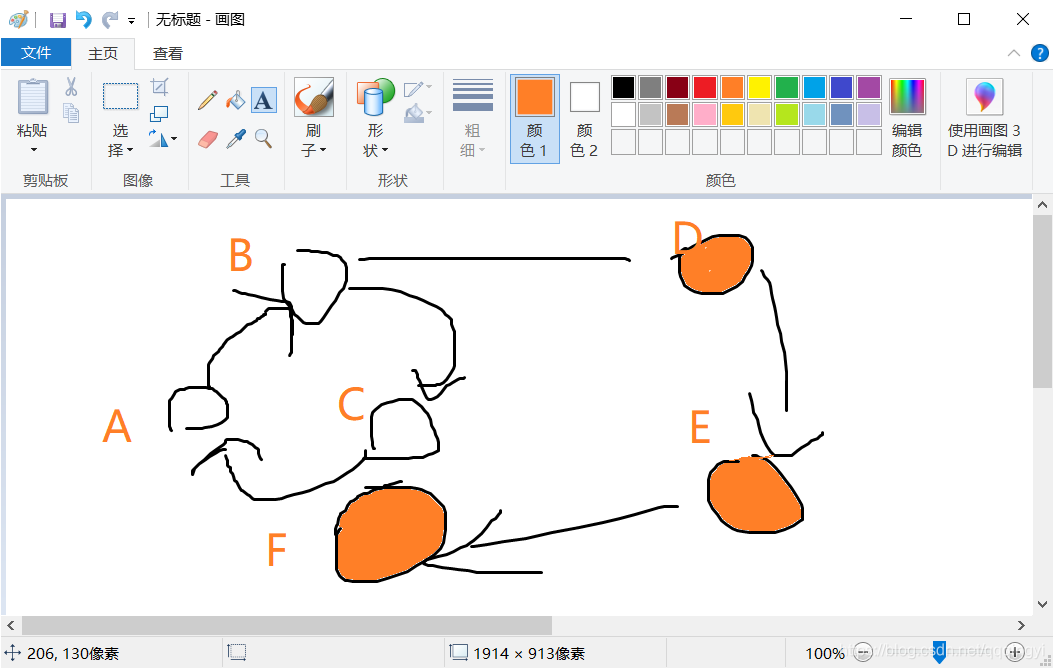
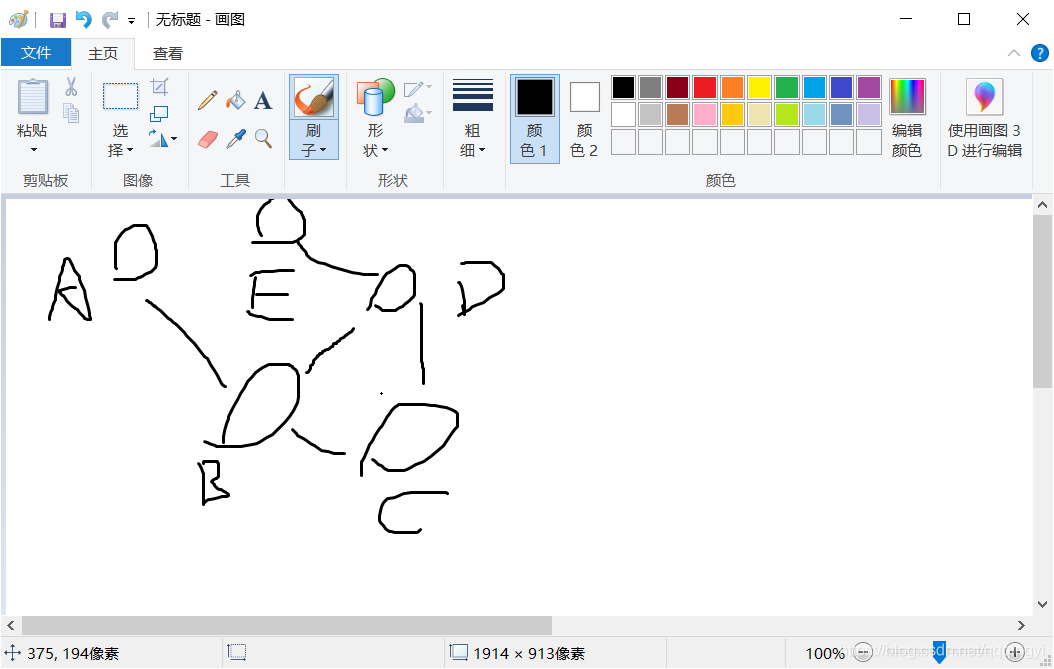
从这张图上可以看出 A B C这三个点都是互相可以走到的 所以他们就是一个联通块 D E F 三个点都是单向能走到 所以D E F 分别为三个联通分量
所以这个图中 一共有 四 个连通分量
然后又引入一个概念 缩点 将连通块中的点当成一个点
可以用来求 连通块问题
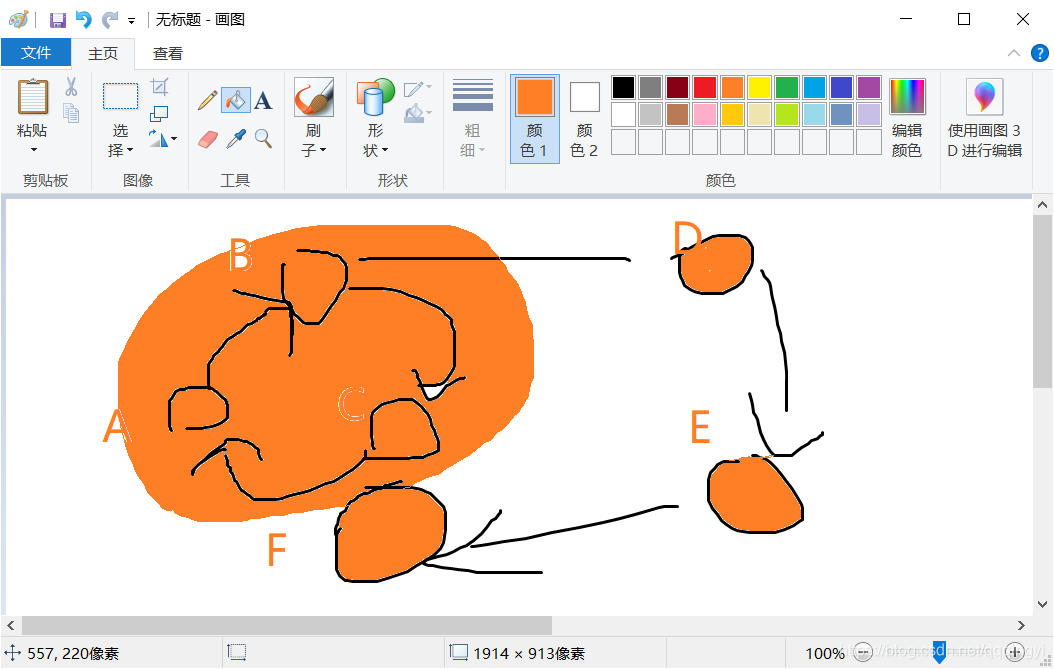
我们知道概念了 该如何去求这个图中有几个连通分量呢
引用时间戳这个概念
A - > B -> D -> E -> F
A -> B -> C
所以ABCDEF的进入时间分别为1 2 6 3 4 5
我们走到 F的时候 发现没有路可以走了 所以没有形成 一个环所以 他自成一个 E D 分别自成一个 走到 C的时候发现可以回到 1 所以他是可以和 A成一个环的 所以 把C的时间戳修改成 A的时间戳 表明 他们是可以走一起的 同样返回的时候 把 B 的时间戳也修改成 与 C已经成功成环的时间戳 即可
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e4 + 10,M = 5e4 + 10;
int head[N],to[M],last[M],cnt;
void add(int a,int b){
to[++cnt] = b;
last[cnt] = head[a];
head[a] = cnt;
}
int n,m;
int toopc[N];
int dfn[N],low[N],sta[N],top,ttime,flag[N],scc_cnt,st_size[N],belong[N];
void dfs(int x){
dfn[x] = low[x] = ++ttime; //两个时间戳 一个记录进入时间 一个记录最后是否是一个时间戳的时间
sta[++top] = x,flag[x] = 1; //记录这个路径中的点
for(int i = head[x]; i != -1; i = last[i]){
int j = to[i];
if(!dfn[j]){
dfs(j);
low[x] = min(low[x],low[j]); //变成 下一个点已经成环的时间戳
}else if(dfn[j] && flag[j]){
low[x] = min(low[x],dfn[j]); //如果此次路劲已经走过了他 那么直接判断即可
}
}
if(low[x] == dfn[x]){
//如果时间戳相同的话 那么这个点就是这个环的起点位置
++scc_cnt;
int y;
int h = 0;
do{
++h;
y = sta[top--];
flag[y] = 0;
belong[y] = scc_cnt; //这个点属于这个环
}while(y != x);
st_size[scc_cnt] = h;
}
}
int main(){
memset(head,-1,sizeof head);
cin >> n >> m;
for(int i = 1; i <= m; i++){
int x,y;
cin >> x >> y;
add(x,y);
}
for(int i = 1; i <= n; i++){
if(!dfn[i]) dfs(i);
}
for(int i = 1; i <= n; i++){
for(int j = head[i]; j != -1; j = last[j]){
int k = to[j];
if(belong[i] != belong[k]){
toopc[belong[i]]++;
}
}
}
int sum = 0;int s = 0;
for(int i = 1; i <= scc_cnt; i++){
if(toopc[i] == 0){
sum += st_size[i];
++s;
}
if(s > 1){
sum = 0;
}
}
cout << sum << endl;
return 0;
}
双连通分量指的是 连通块中的每两个点都有 两条不相交的路径可以走到对方
而去掉图中的一条边 使连通块增加的这个边 叫做桥
去掉 全部与一个点的边 使连通块数量增加的点 叫割点
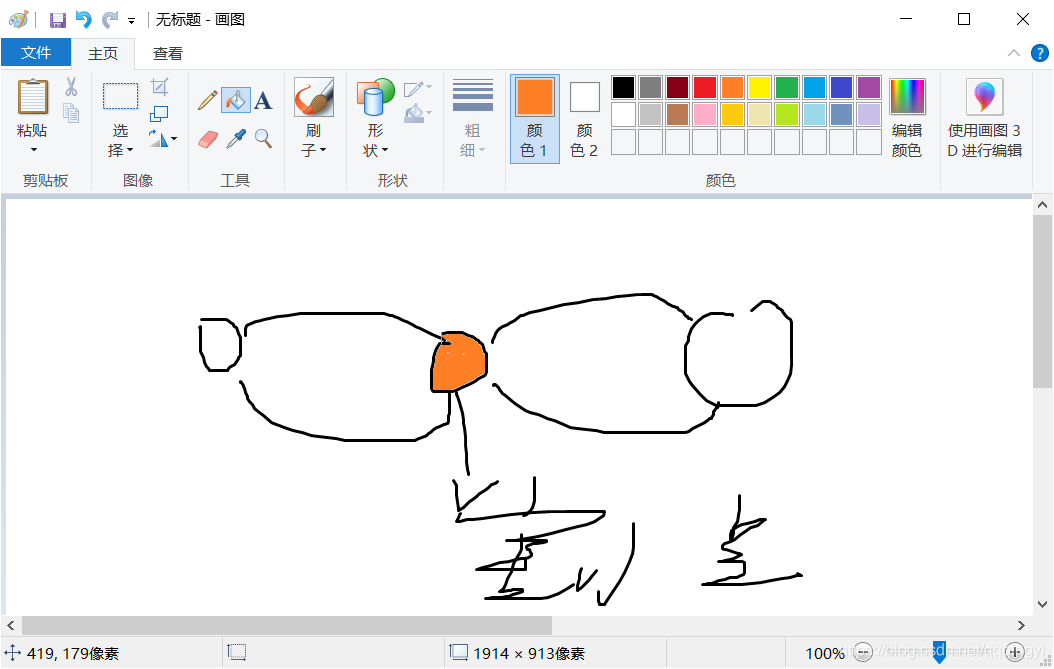
红色的点就是割点
如何去求一个图中的桥呢
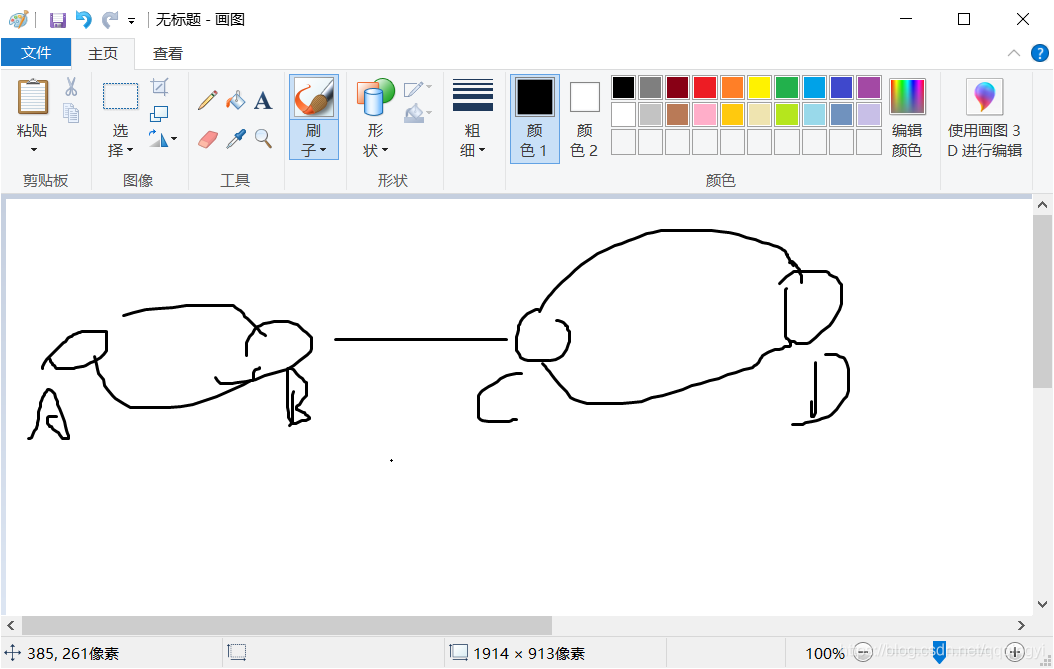
由图推导
A->B->C->D->C 所以C和D是一个环 是一个联通块
但是C -> B 是B -> C 的反向边 所以 C->B不能使ABCD成为同一个双连通块
所以 这个时候 B->C就成为了一个桥同样B->C也是一个桥 所以当
这条边无法是他们成为同一个连通块的时候 就是一个桥;
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e4 + 10,M = 1e5 + 10;
int n,m;
int head[N],to[M],last[M],cnt;
void add(int a,int b){
to[cnt] = b;
last[cnt] = head[a];
head[a] = cnt++;
}
int dfn[N],low[N],sta[N],is_bridge[N],belong[N],toop[N];
int times,top,scc_cnt;
void tarjan(int x,int lastt){
dfn[x] = low[x] = ++times;
sta[++top] = x;
for(int i = head[x]; i != -1; i = last[i]){
int j = to[i];
if(!dfn[j]){
tarjan(j,i);
low[x] = min(low[x],low[j]);
if(dfn[x] < low[j]){
// 如果low[j] > dfn[x] 说明 j 和 x点不是同一连通分量
is_bridge[i] = is_bridge[i ^ 1] = 1;
}
}else if(i != (lastt ^ 1)){
//由于是无向图所以 i + 1 是 i 的反向边 如果 i % 2 == 0
low[x] = min(low[x],dfn[j]); //如果不判断反向边的话 dfn[x] == low[j]
}
}
if(dfn[x] == low[x]){
++scc_cnt;
int y;
do{
y = sta[top--];
belong[y] = scc_cnt;
}while(y != x);
}
}
int main(){
memset(head,-1,sizeof head);
cin >> n >> m;
for(int i = 1; i <= m; i++){
int x,y;
cin >> x >> y;
add(x,y);
add(y,x);
}
tarjan(1,-1);
for(int i = 0; i < cnt; i++){
if(is_bridge[i]){
toop[belong[to[i]]]++;
}
}
int ans = 0;
for(int i = 1; i <= scc_cnt; i++){
if(toop[i] == 1){
ans++;
}
}
cout << (ans + 1) / 2 << endl;
return 0;
}
割点怎么求;
我们照样可以用图来推导
C ->B -> A
我们发现 A自成了一个连通分量 所以A只能 通过 B才能返回到原来的祖先
所以B就是一个割点
同样如果A B 成环的话 A 还是得需要从B才能回到C 所以B还是割点
所以当dfn[i] <= low[j]的时候 那么B就是一个割点
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int N = 1010;
int n,maxn;
int head[N],to[N * 2],last[N * 2],cnt;
void add(int a,int b){
to[++cnt] = b;
last[cnt] = head[a];
head[a] = cnt;
}
vector<int>dcc[N];
int dfn[N],low[N],sta[N],cut[N];
int times,top,root,dcc_cnt;
void tarjan(int x){
dfn[x] = low[x] = ++times;
sta[++top] = x;
int ans = 0;
if(x == root && head[x] == -1){
++dcc_cnt;
dcc[dcc_cnt].push_back(x);
return;
}
for(int i = head[x]; i != -1; i = last[i]){
int j = to[i];
if(!dfn[j]){
tarjan(j);
low[x] = min(low[x],low[j]);
if(dfn[x] <= low[j]){
ans++;
if(x != root || ans > 1) cut[x] = 1; //如果他是根节点的话那么他就没有祖先所以 只有他有两个儿子节点才能变成割点
++dcc_cnt;
int y;
do{
y = sta[top--];
dcc[dcc_cnt].push_back(y);//将割点影响到的点记录下来
}while(y != j); //如果y != x的话 那么割点x就没了,那么后续如果还有连通分量的话 就不成立了
dcc[dcc_cnt].push_back(x);
}
}else low[x] = min(low[x],dfn[j]);
}
}
int main(){
int casse = 0;
while(cin >> n && n){
memset(head,-1,sizeof head);
memset(dfn,0,sizeof dfn);
memset(cut,0,sizeof cut);
maxn = 0,cnt = 0;
dcc_cnt = 0,times = 0,top = 0;
for(int i = 1; i <= n; i++){
int x,y;
cin >> x >> y;
maxn = max(maxn,x);
maxn = max(maxn,y);
add(x,y);
add(y,x);
}
for(root = 1; root <= maxn; root++){
if(!dfn[root]){
tarjan(root);
}
}
int sum = 0;
for(int i = 1; i <= maxn; i++){
if(cut[i] == 1) sum++;
}
cout << sum << endl;
}
return 0;
}