基于线性函数近似的安全强化学习 Safe RL with Linear Function Approximation 翻译 2

论文：Safe Reinforcement Learning with Linear Function Approximation
下载地址：http://proceedings.mlr.press/v139/amani21a/amani21a.pdf
会议/年份：PMLR / 2021

Word版本下载地址（辛辛苦苦打出来的）：https://download.csdn.net/download/baishuiniyaonulia/85863332
本文翻译属于半人工，有错漏请谅解。

摘要、1、2、3

基于线性函数近似的安全强化学习 Safe RL with Linear Function Approximation 翻译 1 —— https://blog.csdn.net/baishuiniyaonulia/article/details/125504660

4. 扩展到随机化的策略选择 Extension to randomized policy selection

第 2 节中介绍的 SLUCB-QVI 只能输出确定性策略。 在本节中，我们表明我们的结果可以扩展到随机策略选择的设置，这在实践中可能是可取的。 随机策略 $\pi :\mathcal{S}\times [H]\to {\Delta }_{\mathcal{A}}$ 将状态和时间步映射到动作上的分布，使得 $a\sim \pi (s,h)$ 是策略 π 建议智能体在处于状态 $s\in \mathcal{S}$ 时在时间步 $h\in [H]$ 执行的动作。 在每个情节 k 和时间步 $h\in [H]$ 中，当处于状态 $s_h^k$ 时，智能体必须从 a 中提取其动作 $a_h^k$ 安全策略 ${\pi }_k\left(s_h^k,h\right)$ 使得$${\mathbb{E}}_{a_h^k\sim {\pi }_k\left(s_h^k,h\right)}{c}_h\left(s_h^k,a_h^k\right)\le \tau$$概率很高。 我们相应地定义了一组未知的安全策略$${\tilde{\Pi }}^{\text{safe }}:=\left\{\pi :\pi (s,h)\in {\Gamma }_h^{\text{safe }}(s),\forall (s,h)\in \mathcal{S}\times [H]\right\}$$

其中 Γ h safe ( s ) : = { θ ∈ Δ A : E a ∼ θ c h ( s , a ) ≤ τ } \Gamma _{h}^{\text{safe}}(s):=\left\{ \theta \in { {\Delta }_{\mathcal{A}}}:{ {\mathbb{E }}_{a\sim\theta }}{ {c}_{h}}(s,a)\le \tau \right\} Γhsafe​(s):={ θ∈ΔA​:Ea∼θ​ch​(s,a)≤τ}。因此，在第 k 回合的时间步 $h\in [H]$ 观察状态 $s_h^k$ 之后，智能体的策略选择必须属于 ${\Gamma }_h^{\text{safe}}(s_h^k)$ 概率很高。在这个公式中，策略 π 的（动作）价值函数定义中的期望值超过了环境和策略 π 的随机性。我们用 ${\tilde{V}}_h^{\pi }$ 和 ${\tilde{Q}}_h^{\pi }$ 来表示它们，以区别于 ${\tilde{V}}_h^{\pi }$ 和 ${\tilde{Q}}_h^{\pi }$ 在 (2) 和 (3) 中定义，用于确定性策略 π。令 ${\pi }_{\ast }$ 为最优安全策略，使得 ${\tilde{V}}_h^{{\pi }_{\ast }}(s):={\tilde{V}}_h^{\ast }(s)=\underset{\pi \in {\tilde{\Pi }}^{\text{safe }}}{\sup }{\tilde{V}}_h^{\pi }(s)$ 对于所有 $(s,h)\in \mathcal{S}\times [H]$。因此，对于所有 $(a,s,h)\in \mathcal{A}\times \mathcal{S}\times [H]$，安全策略的贝尔曼方程 $\pi \in {\tilde{\Pi }}^{\text{safe }}$ 和最优安全策略是

$$\begin{array}{rl}& {\tilde{Q}}_h^{\pi }(s,a)=r_h(s,a)+\left[{\mathbb{P}}_h{\tilde{V}}_{h+1}^{\pi }\right](s,a),\\ & {\tilde{V}}_h^{\pi }(s)={\mathbb{E}}_{a\sim \pi (s,h)}\left[{\tilde{Q}}_h^{\pi }(s,a)\right],\end{array}$$$$\begin{array}{rl}& {\tilde{Q}}_h^{\ast }(s,a)=r_h(s,a)+\left[{\mathbb{P}}_h{\tilde{V}}_{h+1}^{\ast }\right](s,a),\\ & {\tilde{V}}_h^{\ast }(s)={\max }_{\theta \in {\Gamma }_h^{\text{safe }(s)}}{\mathbb{E}}_{a\in \theta }\left[{\tilde{Q}}_h^{\ast }(s,a)\right],\end{array}$$

其中${\tilde{V}}_{H+1}^{\pi }(s)={\tilde{V}}_{H+1}^{\ast }(s)=0$，定义了累积后悔 如 $R_K:=\sum _{k=1}^K{\tilde{V}}_1^{\ast }(s_1^k)-{\tilde{V}}_1^{{\pi }_k}(s_1^k)$。 (11) 中的安全约束定义使我们摆脱了对集合 D ( s ) : = { ϕ ( s , a ) : a ∈ A } \mathcal{D}(s):=\{\phi (s,a):a\in \mathcal{A}\} D(s):={ ϕ(s,a):a∈A} 的星凸假设 （假设 5），这是确定性策略选择方法所必需的。 我们建议对 SLUCB-QVI 进行修改，以适应这种新的配方，称为随机 SLUCB-QVI (RSLUCB-QVI)。 这种新算法还实现了与 SLUCB-QVI 相同阶次的亚线性后悔，即 $\tilde{\mathcal{O}}\left(\kappa \sqrt{d^3{H}^{3}T}\right)$.

虽然与 SLUCB-QVI（参见（1））中考虑的安全约束相比，RSLUCB-QVI 尊重了更温和的安全约束定义（参见（11）），但它仍然比其他现有算法通过随机策略选择解决 CMDP 具有显着优势 （Efroni 等人，2020；Turchetta 等人，2020；Garcelon 等人，2020；Zheng 和 Ratliff，2020；Ding 等人，2020a；Qiu 等人，2020；Ding 等人，2020b；Xu 等人，2020 年；Kalagarla 等人，2020 年）。 首先，这些算法中考虑的安全约束是由低于某个阈值的时间范围内的累积预期成本定义的，而 RSLUCB-QVI 保证在执行动作的每个时间步（而不是时间范围内）产生的预期成本 小于阈值。 其次，即使对于安全约束的这种更宽松的定义，这些算法在约束满足方面所能保证的最好的方法是约束违反次数的亚线性界限，而 RSLUCB-QVI 确保没有约束违反。

4.1. 随机SLUCB-QVI Randomized SLUCB-QVI

我们现在描述算法 2 中总结的 RSLUCB-QVI。令 ${\varphi }^{\theta }(s):={\mathbb{E}}_{a\sim \theta }\varphi (s,a)$。 在每个情节 $k\in [K]$ 中，在第一个循环中，智能体计算所有 $s 的真实未知集 ${\Gamma }_h^{\text{safe}}(s)$ 的估计集 $s\in \mathcal{S}$ 如下：
$${\Gamma }_h^k(s):=\{\theta \in {\Delta }_{\mathcal{A}}:{\mathbb{E}}_{a\sim \theta }\left[\frac{⟨{\Phi }_0(s,\varphi (s,a)),\tilde{\varphi }\left(s,a_0(s)\right)⟩}{{\Vert \varphi \left(s,a_0(s)\right)\Vert }_2}{\tau }_h(s)\right]+\underset{\nu \in {\mathcal{C}}_h^k(s)}{\max }⟨{\Phi }_0^{\perp }\left(s,{\mathbb{E}}_{a\sim \theta }[\varphi (s,a)]\right),\nu ⟩\le \tau \}$$

$$=\left\{\theta \in {\Delta }_{\mathcal{A}}:\frac{⟨{\Phi }_0\left(s,{\varphi }^{\theta }(s)\right),\tilde{\varphi }\left(s,a_0(s)\right)⟩}{{\Vert \varphi \left(s,a_0(s)\right)\Vert }_2}{\tau }_h(s)+⟨{\gamma }_{h,s}^k,{\Phi }_0^{\perp }\left(s,{\varphi }^{\theta }(s)\right)⟩+\beta {\Vert {\Phi }_0^{\perp }\left(s,{\varphi }^{\theta }(s)\right)\Vert }_{{\left({\mathbf{A}}_{h,s}^k\right)}^{-1}}\le \tau \right\}$$

请注意，由于 MDP 的线性结构，我们可以再次通过线性形式$⟨{\tilde{\mathbf{w}}}_h^{\ast },\varphi (s,a)⟩$参数化 ${\tilde{Q}}_h^{\ast }(s,a)$ , 其中 ${\tilde{\mathbf{w}}}_h^{\ast }:={\theta }_h^{\ast }+{\int }_{\mathcal{S}}{\tilde{V}}_{h+1}^{\ast }(s^{\prime })d\mu (s^{\prime })$。 在下一步中，对于所有 $(s,a)\in \mathcal{S}\times \mathcal{A}$，智能体计算$${\tilde{Q}}_h^k(s,a)=⟨{\tilde{\mathbf{w}}}_h^k,\varphi (s,a)⟩+{\kappa }_h(s)\beta {\Vert \varphi (s,a)\Vert }_{{\left({\mathbf{A}}_h^k\right)}^{-1}}$$

其中 ${\tilde{\mathbf{w}}}_h^{\ast }:={\left({\mathbf{A}}_h^k\right)}^{-1}widetilde{\mathbf{b}}_h^k$ 是由 Gram 矩阵 $ 计算的 ${\tilde{\mathbf{w}}}_h^{\ast }$ 的正则化最小二乘估计量\mathbf{A}_{h}^{k}$ 和 ${\tilde{\mathbf{b}}}_h^k:=\sum _{j=1}^{k-1}{\varphi }_h^j\left[r_h^j+\min \left\{{\max }_{\theta \in {\Gamma }_{h+1}^k\left(s_{h+1}^j\right)}{\mathbb{E}}_{a\sim \theta }\left[{\tilde{Q}}_{h+1}^k\left(s_{h+1}^j,a\right)\right],H\right\}\right]$。在第一个循环中的这些计算之后，智能体从分布 ${\Gamma }_h^k\left(s_h^k\right)$ 中绘制动作 $a_h^k$在第二个循环中。定义 ${\tilde{V}}_h^k(s):=\min \left\{{\max }_{\theta \in {\Gamma }_h^k(s)}{\mathbb{E}}_{a\sim \theta }\left[{\tilde{Q}}_h^k(s,a)\right],H\right\}$ , 和 ${\mathcal{E}}_3:=\{|⟨{\tilde{\mathbf{w}}}_h^k,\varphi (s,a)⟩-{\tilde{Q}}_h^{\pi }(s,a)-\left[{\mathbb{P}}_h{\tilde{V}}_{h+1}^{\pi }-{\tilde{V}}_{h+1}^k\right](s,a)|\le \beta {\Vert \varphi (s,a)\Vert }_{{\left({\mathbf{A}}_h^k\right)}^{-1}},\forall (a,s,h,k)\in \mathcal{A}\times \mathcal{S}\times [H]\times [K]\}$。

可以很容易地证明，定理 2 中所述的结果适用于专注于随机策略的设置，即在假设 1、2、3 和 4 下，并且根据定理 1 中 β 的定义，概率至少为 $1-2\delta$，事件 $\tilde{\mathcal{E}}:={\mathcal{E}}_1\bigcap {\mathcal{E}}_3$ 成立。 因此，作为命题 1 的直接结论，保证以 ${\mathcal{E}}_1$ 为条件，${\Gamma }_h^k(s)$ 内的所有策略是安全的，即 ${\Gamma }_h^k(s)\subset {\Gamma }_h^{\text{safe}}(s)$。 现在，在下面的引理中，我们量化了 ${\kappa }_h(s)$。

引理 2 （面对 RSLUCB-QVI 安全约束的乐观态度） Lemma 2 (Optimism in the face of safety constraint in RSLUCB-QVI)

令 ${\kappa }_h(s):=\frac{2H}{\tau -{\tau }_h(s)}+1$ 和假设 1,2,3 ,4 保持。 然后，以事件 $\tilde{\mathcal{E}}$ 为条件，它认为 ${\tilde{V}}_h^{\ast }(s)\le {\tilde{V}}_h^k(s),\forall (s,h,k)\in \mathcal{S}\times [H]\times [K]$。

证明包含在附录 B.1 中。 使用引理 2，我们证明 ${\tilde{Q}}_h^{\ast }(s,a)\le {\tilde{Q}}_h^k(s,a)$, $forall(a,s,h,k)\in \mathcal{A}\times \mathcal{S}\times [H]\times [K]$。 这突出了 RSLUCB-QVI 的 UCB 特性，使我们能够利用不安全的 LSVI-UCB (Jin et al., 2020) 的标准分析来建立后悔界。

定理 3 （RSLUCB-QVI 的遗憾） Theorem 3 (Regret of RSLUCB-QVI)

在假设 1、2、3 和 4 下，存在一个绝对常数 $c_{\beta }>0$ 使得对于任何固定的 $\delta \in (0,1/3)$，并且 定理 1 中 β 的定义，如果我们设 ${\kappa }_h(s):=\frac{2H}{\tau -{\tau }_h(s)}+1$，

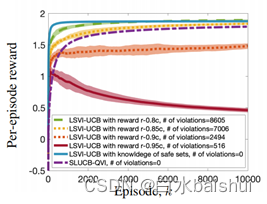
图 1. SLUCB-QVI 与不安全的最先进技术的比较验证：1) 当 LSVI-UCB (Jin et al., 2020) 知道 ${\gamma }_h^{\ast }$ ，它按预期优于 SLUCB-QVI（不知道 ${\gamma }_h^{\ast }$）； 2）当 LSVI-UCB 不知道 ${\gamma }_h^{\ast }$（如 SLUCB-QVI 的情况）并且其目标是最大化 $r-{\lambda }^{\prime }c$ 而不是 r ，较大的 ${\lambda }^{\prime }$ 导致每回合奖励和约束违规次数较小，而 SLUCB-QVI 的约束违规次数为零。

然后以至少 $1-3\delta$ 的概率，它认为 $R_K\le 2H\sqrt{T\log \left(\frac{dT}{\delta }\right)}+2(1+\kappa )\beta \sqrt{2dHT\log \left(1+\frac{K}{d\lambda }\right)}$，其中 $\kappa :={\max }_{(s,h)\in \mathcal{S}\times [H]}{\kappa }_h(s)$。证明见附录 B.2。

5. 实验 Experiments

在本节中，我们提出数值模拟来补充和证实我们的理论发现。 我们评估 SLUCB-QVI 在合成环境中的性能，并在 OpenAI Gym 的 Frozen Lake 环境中实施 RSLUCB-QVI（Brockman 等人，2016 年）。

5.1. 合成环境中的SLUCB-QVI SLUCB-QVI on synthetic environments

图 1 中显示的结果描述了 20 次实现的平均值，为此我们选择了 $\delta =0.01,\sigma =0.01,\lambda =1,d=5,\tau =0.5,H=3$ 和 $K= 10000 美元。 参数 { θ h ∗ } h ∈ [ H ] { {\left\{ \theta _{h}^{*} \right\}}_{h\in [H]}} { θh∗​}h∈[H]​ 和 { γ h ∗ } h ∈ [ H ] { {\left\{ \gamma _{h}^ {*} \right\}}_{h\in [H]}} { γh∗​}h∈[H]​ 来自 $\mathcal{N}\left(0,I_d\right)$。 为了调优参数 { μ h ∗ ( . ) } h ∈ [ H ] { {\left\{ \mu _{h}^{*}(.) \right\}}_{h\in [H]}} { μh∗​(.)}h∈[H]​ 和特征图 $\varphi$ 这样 它们与假设 1 兼容，我们认为特征空间 { ϕ ( s , a ) : ( s , a ) ∈ S × A } \{\phi (s,a):(s,a)\in \mathcal{S}\times \mathcal{A}\} { ϕ(s,a):(s,a)∈S×A} 是一个子集 d 维单纯形和 ${\mathbf{e}}_i^{\top }{\mu }_h^{\ast }(.)$ 是对 $\mathcal{S}$ 的任意概率测度 所有$i\in [d]$。 这保证了假设 1 成立。

在 SLUCB-QVI 的第一个循环（第 6 行）中计算安全集 ${\mathcal{A}}_h^k(s)$，然后选择最大化线性函数的动作（在特征映射 $ \phi $) 在特征空间 ${\mathcal{D}}_h^k\left(s_h^k\right):=\left\{\varphi \left(s_h^k,a\right):a\in {\mathcal{A}}_h^k\left(s_h^k\right)\right\}$ 在第二个循环中 （第 10 行）。 不幸的是，即使特征空间 { ϕ ( s , a ) : ( s , a ) ∈ S × A } \{\phi (s,a):(s,a)\in \mathcal{S}\times \mathcal{A}\} { ϕ(s,a):(s,a)∈S×A} 是凸的，集合 ${\mathcal{D}}_h^k\left(s_h^k\right)$ 可以具有难以最大化线性函数的形式。 在我们的实验中，我们定义映射 $\phi $ 使得集合 $\mathcal{D}(s)$ 在 $\varphi \left(s,a_0(s)\right)$ 与 $N=100$ （见定义 1），因此，我们可以证明 SLUCB-QVI 的第 10 行中的优化问题可以有效地解决（见附录 C 的证明）。

定义1 （有限星凸集） Definition 1 (Finite star convex set)

一个围绕 $x_0\in {\mathbb{R}}^d$ 的星形凸集 $\mathcal{D}$ 是有限的，如果存在有限多个向量 { x i } i = 1 N \left \{ { {\mathbf{x}}_{i}} \right\}_{i=1}^{N} { xi​}i=1N​ 使得 $\mathcal{D}={\bigcup }_{i=1}^N\left[{\mathbf{x}}_0,{\mathbf{x}}_i\right]$，其中 $\left[{\mathbf{x}}_0,{\mathbf{x}}_i\right]$ 是连接 ${\mathbf{x}}_0$ 和 ${\mathbf{x}的线}_i$。

图 1 描绘了 SLUCB-QVI 的平均每回合奖励，并将其与基线进行了比较，并强调了 SLUCB-QVI 在尊重所有时间步的安全约束方面的价值。具体来说，我们将 SLUCB-QVI 与 1) LSVI-UCB (Jin et al., 2020) 进行比较，因为它具有安全约束知识，即 ${\gamma }_h^{\ast }$； 2) LSVI-UCB，当它不知道 ${\gamma }_h^{\ast }$（如 SLUCB-QVI 的情况）并且其目标是最大化函数 $r-{\lambda }^{\prime }c$，约束被推入目标函数，对于 ${\lambda }^{\prime }=0.8,0.85,0.9$ 和 0.95 的不同值。因此，通过低奖励不鼓励采取代价高昂的行动。该图验证了具有 ${\gamma }_h^{\ast }$ 知识的 LSVI-UCB 在不了解 ${\gamma }_h^{\ast }$ 的情况下按预期优于 SLUCB-QVI。此外，当 LSVI-UCB 试图最大化 $r-{\lambda }^{\prime }c$（不知道 ${\gamma }_h^{\ast }$) 而 SLUCB-QVI 的约束违反次数为零。

5.2. 冰冻湖环境下的RSLUCB-QVI RSLUCB-QVI on Frozen Lake environment

我们评估了 RSLUCB-QVI 在 Frozen Lake 环境中的性能。 智能体寻求在 10 × 10 2D 地图中达到目标（图 2a），同时避免危险。

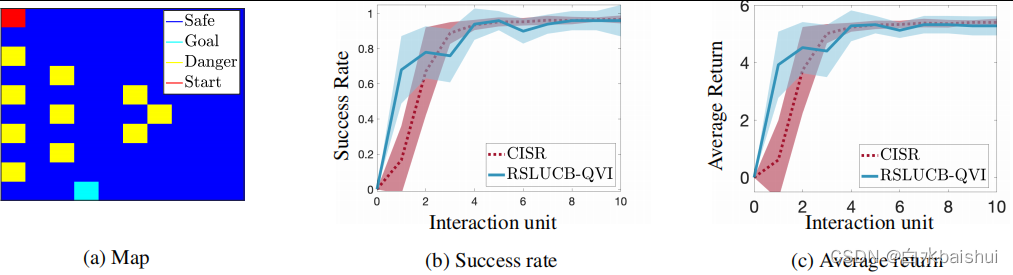
图 2.RSLUCB-QVI 和 CISR (Turchetta et al., 2020) 在 Frozen Lake 环境中的比较。

在每个时间步，智能体可以向四个方向移动，即 A = { a 1 : left,  a 2 : right,  a 3 : down,  a 4 : up } \mathcal{A}=\{ { {a}_{1}}:\text{left, }{ {a}_{2}}:\text{right, }{ {a}_{3}}:\text{down, }{ {a}_{4}}:\text{up}\} A={ a1​:left, a2​:right, a3​:down, a4​:up}。它以 0.9 的概率沿所需方向移动，以 0.05 的概率沿任一正交方向移动。我们设$H=1000,K=10,d=|\mathcal{S}|=100$, AND${\mu }^{\ast }(s)\sim \mathcal{N}\left(0,I_d\right)$ for all s ∈ S = { s 1 , … , s 100 } s\in \mathcal{S}=\left\{ { {s}_{1}},\ldots ,{ {s}_{100}} \right\} s∈S={ s1​,…,s100​}。然后，我们通过求解一组线性方程来正确指定所有 $(s,a)\in \mathcal{S}\times \mathcal{A}$ 的特征映射 $\varphi (s,a)$，使得转换尊重上述环境的细节。为了将避免危险的要求解释为形式 (11) 的约束，我们将 ${\gamma }^{\ast }$ 和 $\tau $ 调整如下：执行动作的成本 $a\in \状态 $s\in \mathcal{S}$ 处的 mathcal{A}$ 是智能体移动到危险状态之一的概率。因此，安全策略确保移动到危险状态的概率的期望值是一个小值。为此，我们设置 ${\gamma }^{\ast }=\sum _{s\in \text{ Danger states }}{\mu }^{\ast }(s)$ 和$\tau =0.1$。此外，对于每个状态 $s\in \mathcal{S}$，将一个安全动作，即导致具有小概率（$\tau =0.1$）的危险状态之一的游戏给予智能体。我们求解一组线性方程来调整 ${\theta }^{\ast }$，使得在每个状态 $s\in \mathcal{S}$，通向最接近目标的状态的方向state 给 agent 奖励 1，而玩其他三个方向给它奖励 0.01。该模型说服智能体朝着目标前进。

在指定特征图 $\varphi$ 并调整所有参数后，我们为 10 个交互单元（episodes）（即 $K=10$）实现了 RSLUCB-QVI，每个交互单元由 1000 个时间步（horizon）组成，即 $H= 1000 美元）。 在每个交互单元（情节）期间和每次移动之后，智能体可以最终处于以下三种状态之一：1）目标，导致交互单元成功终止； 2) 危险，导致交互单元出现故障并随之终止； 3）安全。 智能体达到目标会收到 6 的回报，否则会收到 0.01。

在图 2 中，我们报告了超过 20 个智能体的平均成功率和回报，我们为每个智能体实施了 10 次 RSLUCB-QVI，并将我们的结果与 (Turchetta et al., 2020) 提出的 CISR 的结果进行了比较，其中教师提供了帮助 智能体人通过干预来选择安全的行动。 虽然 RSLUCB-QVI 和 CISR 这两种方法的性能相当，但要考虑的重要一点是，CISR 中的每个交互单元（情节）由 10000 个时间步长组成，而在 RSLUCB-QVI 中这个数字是 1000 个。 值得注意的是，RSLUCB-QVI 的学习率比 CISR 快。 同样值得注意的是，我们在使用优化干预时将 RSLUCB-QVI 与 CISR 进行了比较，与其他类型的干预相比，它给出了最好的结果。

6. 结论 Conclusion

在本文中，我们开发了 SLUCB-QVI 和 RSLUCB-QVI，这两种安全 RL 算法在有限水平线性 MDP 的设置中。 对于这些算法，我们提供了次线性遗憾边界 $\tilde{\mathcal{O}}\left(\kappa \sqrt{d^3{H}^{3}T}\right)$，其中 H 是每集的持续时间，d 是特征映射的维度，κ 是表征安全约束的常数，$T=KH$ 是动作戏的总数。 我们证明了它们很有可能永远不会违反未知的安全约束。 最后，我们分别在合成和 Frozen Lake 环境中实现了 SLUCB-QVI 和 RSLUCB-QVI，这证实了我们的算法具有与了解安全约束或利用现有技术的算法相当的性能 帮助代理人避免不安全行为的教师建议。