二元分类(Binary Classfication)
分类,一种方法是使用线性回归,将所有大于0.5的预测映射为1,将所有小于0.5的预测映射为0。然而,这种方法并不能很好地工作,因为分类实际上不是一个线性函数。
分类问题和回归问题一样,只是我们现在想要预测的值只有少量离散值。现在,我们将使用二元分类问题,其中y只能有两个值,0和1。
如:
y∈{0,1},0代表良性肿瘤,1代表恶性肿瘤
收到一封邮件,0代表是正常邮件,1代表是垃圾邮件
逻辑回归(Logistic Regression)
线性回归,是一种预测算法;而Logistic回归并不是预测算法,而是一种分类算法,用于二分类的问题,也就是输出结果不是0就是1。
Sigmoid函数
忽略y是离散值这一事实来处理分类问题,并使用线性回归算法来尝试预测给定x的y。然而,构造出这种方法性能非常差。所以使用Sigmoid函数来表示。
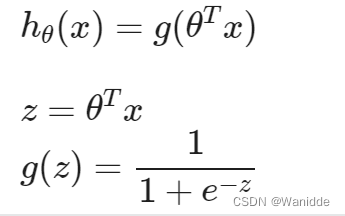
代码:
#计算sigmoid
def sigmoid(z):
return 1 / (1 + np.exp(-z))
#绘制sigmoid图像
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(np.arange(-10, 10, step=0.01),
sigmoid(np.arange(-10, 10, step=0.01)))
ax.set_ylim((-0.1,1.1))
ax.set_xlabel('z', fontsize=18)
ax.set_ylabel('g(z)', fontsize=18)
ax.set_title('sigmoid function', fontsize=18)
plt.show()是输出1的概率。如
表示的是70%的概率输出1。
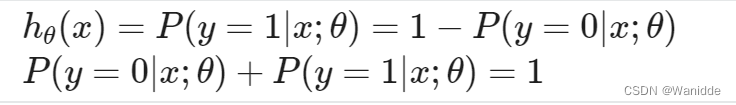
s型曲线,如下图:
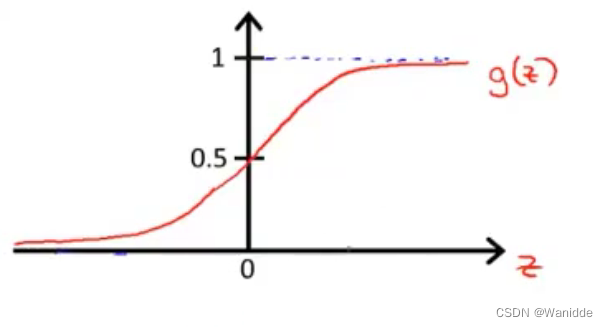
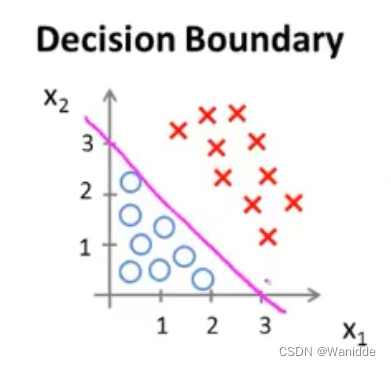
决策界限(Decision Boundary)
决策界限就是将 y=0 和 y=1 划分开来的一条线。
如,
,则决策界限如下图:
为了得到离散的0或1分类,我们可以将假设函数的输出翻译为
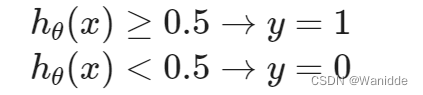
逻辑方程g则表现为
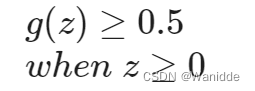
如果我们输入的g是

求决策边界:令

代码:
#画决策曲线
plotting_x1 = np.linspace(30, 100, 100) #均分指令
plotting_h1 = (-result[0][0] - result[0][1] * plotting_x1) / result[0][2]
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(plotting_x1, plotting_h1, 'y', label='Prediction')
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x',label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()代价函数(Cost Function)
我们不能使用与线性回归相同的成本函数,因为逻辑函数输出是会波动的,可能会找不到全局最优。换句话说,它不是一个凸函数。
Logistic回归的成本函数be like:
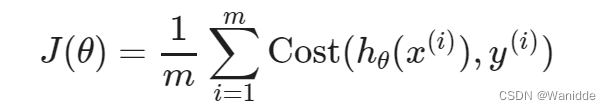
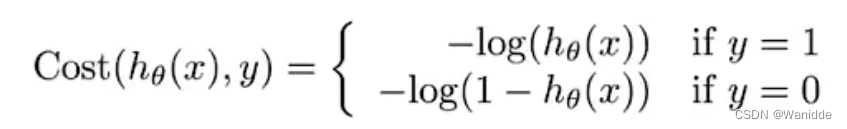
当y=1时:如果y为1,那么如果我们的假设函数输出1,那么成本函数将是0。如果我们的假设接近0,那么成本函数将接近无穷大。

y=0时:如果y为0,那么如果我们的假设函数也输出0,那么成本函数将为0。如果我们的假设接近1,那么代价函数将接近无穷大。
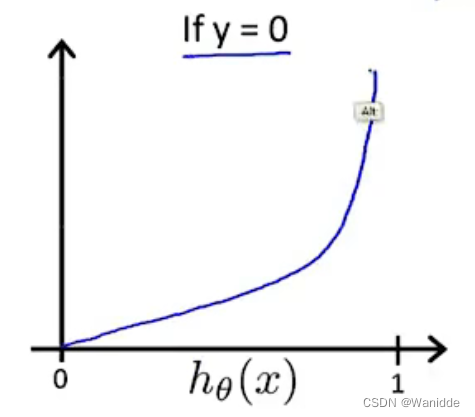
我们可以将代价函数合并成一个式子:
![]()
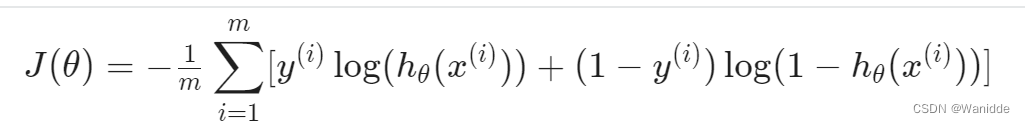
代码:
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1-y), np.log(1 - sigmoid(X * theta.T)))
return np.sum(first - second) / (len(X))
#初始化theta,X,y
#加一列常数列
data.insert(0, 'ones', 1)
#初始化X,y,θ
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]
theta = np.zeros(3)
#转换X,y的类型
X = np.array(X.values)
y = np.array(y.values)
#计算代价
cost(theta,X,y)梯度下降
logistic回归仍然可以使用梯度下降来求解min(J(θ))。
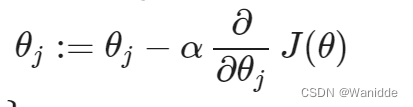
求导后:
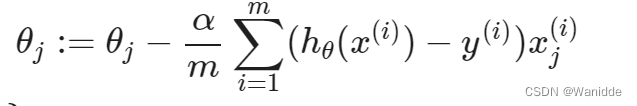
注:此算法与线性回归中的梯度下降相同,仍需同时更新所有θ的值。
代码:
#实现梯度计算的函数
def gradient(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
#误差即假设函数,h(X) - y
error = sigmoid(X * theta.T) -y
for i in range(parameters):
term = np.multiply(error, X[:,i])
grad[i] = np.sum(term) / (len(X))
return grad矢量化实现:
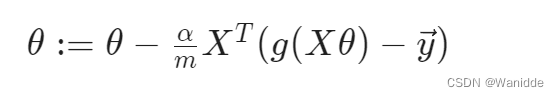
“Conjugate gradient”、“BFGS”和“L-BFGS”是更复杂、更快的优化θ的方法,可以用来代替梯度下降。可以使用封装好的函数实现。
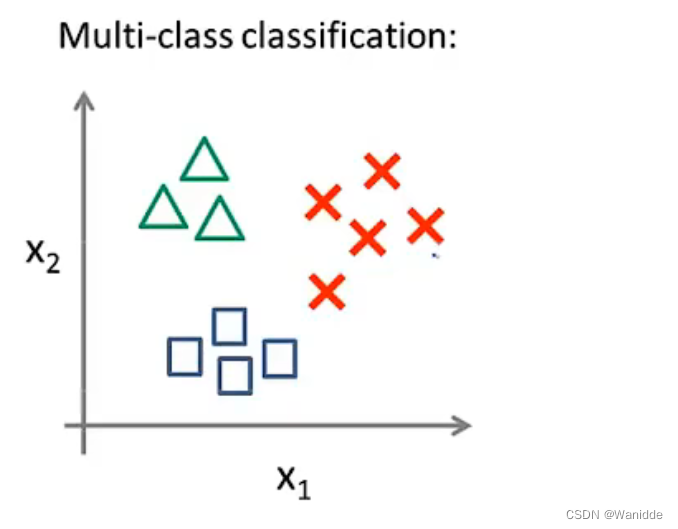
多元分类:一对多(Multiclass Classification)
当我们有两个以上的类别时,我们将对数据进行分类。我们将扩展定义不再是y={0,1},而是y={0,1…n}。我们的假设函数如下:
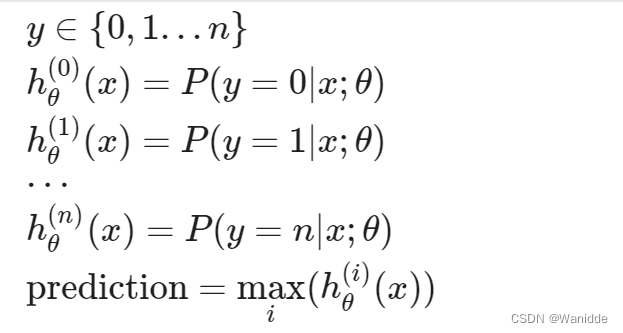
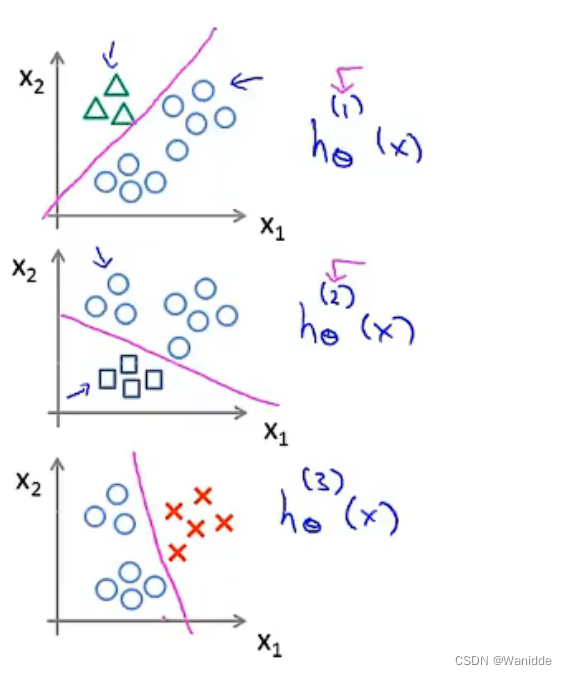
思路:我们基本上是选择一个类,然后将所有其他类合并到一个单独的第二个类。我们反复这样做,对每个案例应用二元逻辑回归,然后使用返回最大值的假设作为我们的预测。
例:
过拟合与欠拟合
欠拟合:是函数不够复杂,无法很好的描述已知数据和预测未知数据。
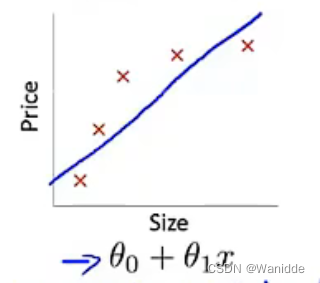
过拟合:在拟合过程中我们会增加参数θ来更好的打到拟合的效果,但如果为了拟合更好添加过多的θ就会出现问题,虽然可以将已知数据很好的表示出来,都是对新数据的预测效果则不尽人意。如下图,图一的拟合效果刚好,而图二则过度拟合。
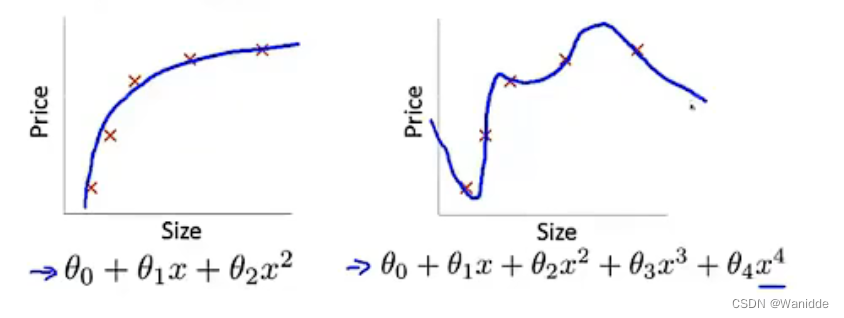 ,
,
过拟合这个术语既适用于线性回归,也适用于逻辑回归。
解决过拟合问题主要有两种方法:
1.减少参数的个数
- 手动选择要保留的功能。
- 使用模型选择算法
2.正则化
- 减少θ的个数
正则化代价函数
如果我们的假设函数过拟合,我们可以通过增加它们的代价来减少函数中某些项的权重。
如我们想要修改,我们想要消除θ3和θ4的影响,我们可以修改代价函数为:
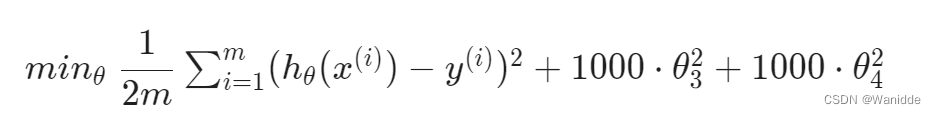
为了使代价函数趋于0,必须减小θ3和θ4的值使之趋于0。
正则化的代价函数:
λ是学习率,正则化参数。它决定了θ参数的代价增大了多少。
使用上述代价函数和求和,我们可以平滑假设函数的输出,以减少过拟合。

代码:
#实现正则化的代价函数
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1-y), np.log(1 - sigmoid(X * theta.T)))
reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
return np.sum(first - second) / len(X) + reg
#初始化X, y,theta
cols = data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]
theta2 = np.zeros(cols-1)
#进行类型转换
X2 = np.array(X2.values)
y2 = np.array(y2.values)
#λ设为1
learningRate = 1
#计算初试代价
costReg(theta2, X2, y2, learningRate)线性回归的正则化(Regularized Linear Regression)
梯度下降法:
我们修改梯度下降函数,因为我们不用正则化θ0,如下:
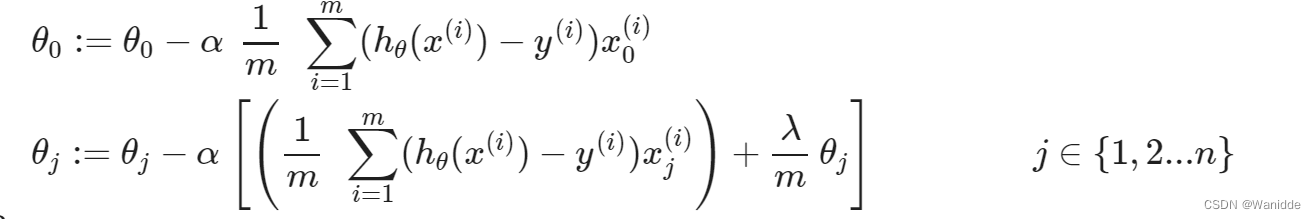
可以合并一下:
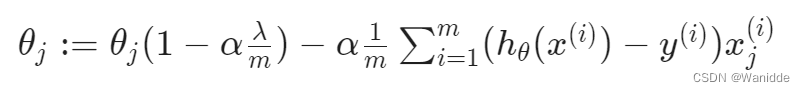
在上式中,永远小于1,可以把它看做是θj的减小。
代码:
#实现正则化的梯度下降
def gradientReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:,i])
if(i == 0):
grad[i] = np.sum(term) / len(X)
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
return grad
正规方程法:
正规方程是使用非迭代法方程的替代方法来处理正则化,要添加正则化,方程与原始方程相同,只是我们在括号内添加了另一项:
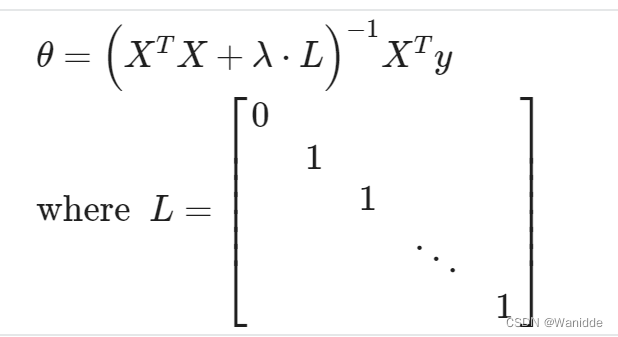
Logistic回归正则化(Regularized Logistic Regression)
我们可以用与线性回归相似的方法来正则化逻辑回归,可以避免过拟合。下图显示了由红线显示的正则化函数与由蓝线表示的非正则化函数相比,过度拟合的可能性更小。

逻辑回归的代价函数为:
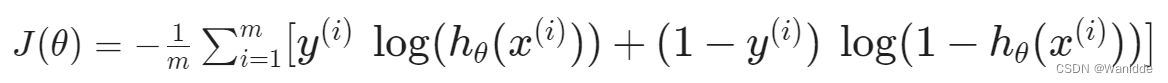
我们可以通过在末尾添加一项来正则化这个方程: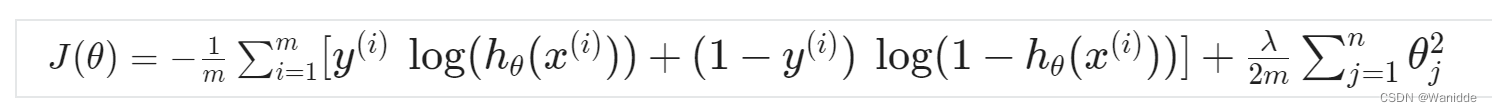
表示明确排除偏差项。
梯度下降的逻辑回归正则化:

学习参考:吴恩达机器学习