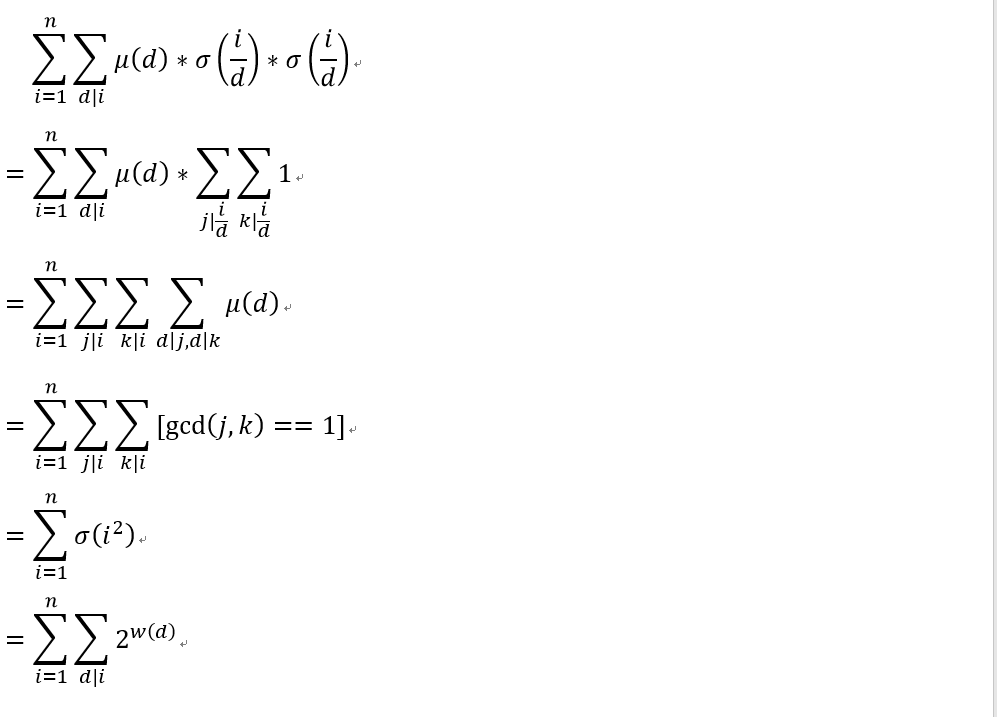Function
题目背景:
分析:数论 + 莫比乌斯反演
将这种丧病的题出到T1,也就这个出题人想的出来······这道题的本质其实是spoj的divcnt2,现在考虑直接推式子······
w(d)表示d的质因数个数,这一步的转化我们这么考虑,对于i2的约数,可以被分为两类,是i的约数也是i2的约数,是i2的约数,但不是i的约数,那么我们考虑对于i的一个约数x,显然,x的每一个质因数的次幂,一定小于等于i的对应的质因数的次幂,那么我们对于x的某一个质因数的次幂加上i的对应质因数的次幂,即:pb能整除x,pa能整除i,那么对于x * pa一定能够对应一个i2的约数,并且这个数一定不会是i的约数,考虑这意味着什么,我们可以对于x任意包含的一个质因数集合,加上对应的在i中的幂次,一定都可以得到一个i2的约数,并且不是i的约数,但是这个质因数x一定要原本包含,那么也就是x的可行的组成集合的元素为w(d)个,那么,可行的选择就有2w(d)种。我们可以发现:
考虑2w(d)的本质,相当于选择一个d的质因数集合,也就是d的不含平方质因子的因数的个数,考虑这类数的相同点就是莫比乌斯函数的值不为0,那么我们直接加莫比乌斯函数值的平方就好了,那么于是就化成了
g为右半边的式子,我们可以发现g(n)相当于1 ~ n的约数个数之和,那么我们可以通过线筛求出,也可以用sqrt(n)的时间直接计算,同样的对于左半边的式子相当于是莫比乌斯函数的平方的前缀和,考虑如何快速求解,我们可以发现原式就是求1 ~ n中不含有平方因子的数的个数,那么我们考虑容斥一下,用所有数先减去一个质数的平方的的倍数,再加上两个质数之积的平方的倍数,减去三个质数之积的平方的倍数······这也就相当于利用莫比乌斯函数容斥一下了所以我们可以得到
所以我们同样可以结合预处理和根号时间计算,考虑类似杜教筛的复杂度分析,我们可以知道预处理n2/3是最优的那么最后的复杂度就是O(n2/3)
Source:
/*
created by scarlyw
*/
#include <cstdio>
#include <string>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
#include <cctype>
#include <vector>
#include <set>
#include <queue>
#include <ctime>
#include <bitset>
inline char read() {
static const int IN_LEN = 1024 * 1024;
static char buf[IN_LEN], *s, *t;
if (s == t) {
t = (s = buf) + fread(buf, 1, IN_LEN, stdin);
if (s == t) return -1;
}
return *s++;
}
///*
template<class T>
inline void R(T &x) {
static char c;
static bool iosig;
for (c = read(), iosig = false; !isdigit(c); c = read()) {
if (c == -1) return ;
if (c == '-') iosig = true;
}
for (x = 0; isdigit(c); c = read())
x = ((x << 2) + x << 1) + (c ^ '0');
if (iosig) x = -x;
}
//*/
const int OUT_LEN = 1024 * 1024;
char obuf[OUT_LEN], *oh = obuf;
inline void write_char(char c) {
if (oh == obuf + OUT_LEN) fwrite(obuf, 1, OUT_LEN, stdout), oh = obuf;
*oh++ = c;
}
template<class T>
inline void W(T x) {
static int buf[30], cnt;
if (x == 0) write_char('0');
else {
if (x < 0) write_char('-'), x = -x;
for (cnt = 0; x; x /= 10) buf[++cnt] = x % 10 + 48;
while (cnt) write_char(buf[cnt--]);
}
}
inline void flush() {
fwrite(obuf, 1, oh - obuf, stdout);
}
/*
template<class T>
inline void R(T &x) {
static char c;
static bool iosig;
for (c = getchar(), iosig = false; !isdigit(c); c = getchar())
if (c == '-') iosig = true;
for (x = 0; isdigit(c); c = getchar())
x = ((x << 2) + x << 1) + (c ^ '0');
if (iosig) x = -x;
}
//*/
const int MAXN = 1000000 + 10;
int prime_cnt, t, cur;
int prime[MAXN], min_cnt[MAXN];
long long miu[MAXN], sum[MAXN], f[MAXN];
bool not_prime[MAXN];
inline void seive() {
not_prime[1] = true, miu[1] = 1, sum[1] = 1;
for (int i = 2; i < MAXN; ++i) {
if (!not_prime[i]) {
prime[++prime_cnt] = i, miu[i] = -1;
sum[i] = 2, min_cnt[i] = 1;
}
for (int j = 1; j <= prime_cnt && prime[j] * i < MAXN; ++j) {
int cur = prime[j] * i;
if (i % prime[j]) {
miu[cur] = -miu[i], not_prime[cur] = true;
sum[cur] = sum[i] * 2, min_cnt[cur] = 1;
} else {
miu[cur] = 0, not_prime[cur] = true;
min_cnt[cur] = min_cnt[i] + 1;
sum[cur] = sum[i] / min_cnt[cur] * (min_cnt[cur] + 1);
break ;
}
}
}
for (int i = 1; i < MAXN; ++i)
f[i] += f[i - 1] + miu[i] * miu[i], sum[i] += sum[i - 1];
}
inline long long get_miu(int cur) {
if (cur < MAXN) return f[cur];
long long ans = 0;
for (int i = 1, end = sqrt(cur); i <= end; ++i)
ans += miu[i] * (cur / i / i);
return ans;
}
inline long long get_sum(long long cur) {
if (cur < MAXN) return sum[cur];
long long ans = 0;
for (int i = 1, last; i <= cur; i = last + 1) {
last = cur / (cur / i);
ans += (long long)(last - i + 1) * (long long)(cur / i);
}
return ans;
}
inline void solve(long long cur) {
long long ans = 0;
for (int i = 1, last; i <= cur; i = last + 1) {
last = cur / (cur / i);
ans += (get_miu(last) - get_miu(i - 1)) * get_sum(cur / i);
}
W(ans), write_char('\n');
}
int main() {
freopen("function.in", "r", stdin);
freopen("function.out", "w", stdout);
R(t), seive();
while (t--) R(cur), solve(cur);
flush();
return 0;
}