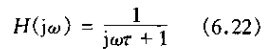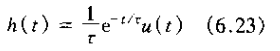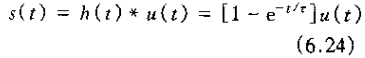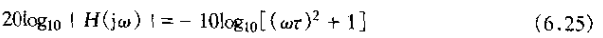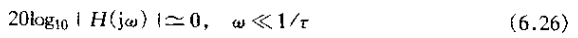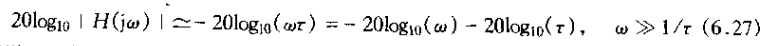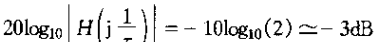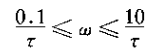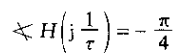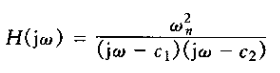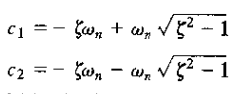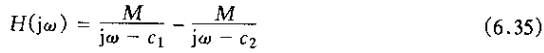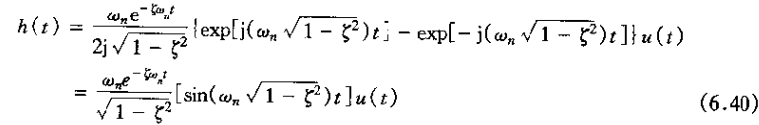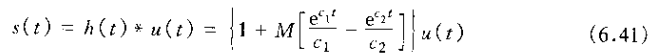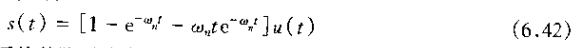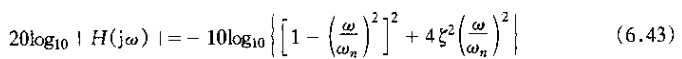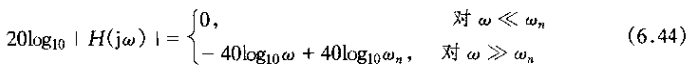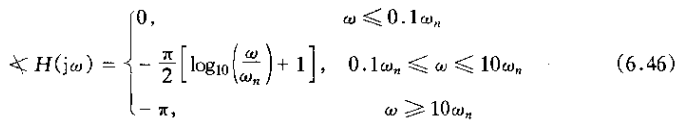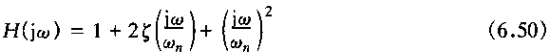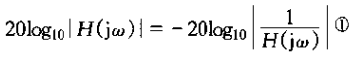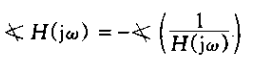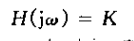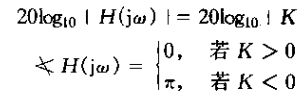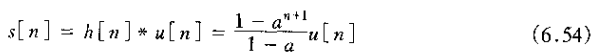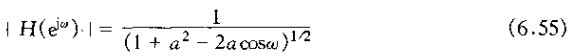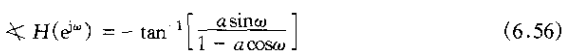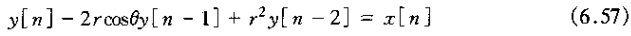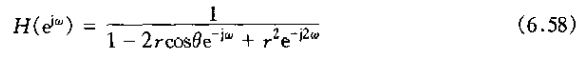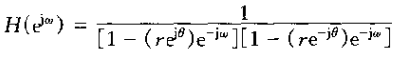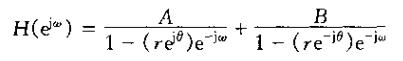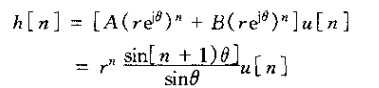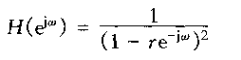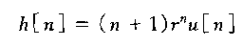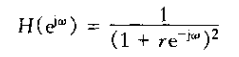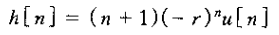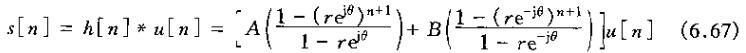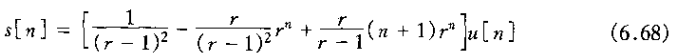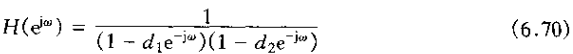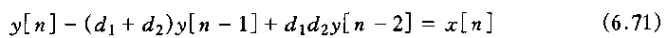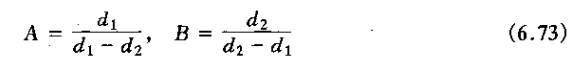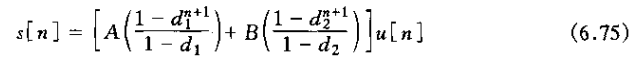注:本博客是基于奥本海姆《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、一阶与二阶连续时间系统
一)、一阶连续时间系统
1、对于一个一阶系统,其微分方程往往表示成下列形式:
区中t是一个系数。相应的一阶系统的频率响应是
其单位冲激响应是
系统的阶跃响应为
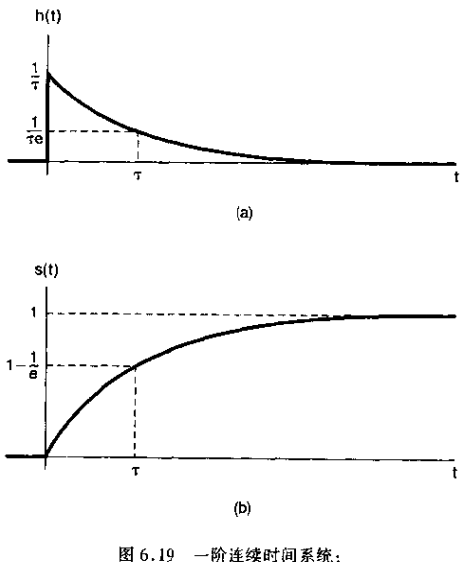
这些都分别回执图6.19)a)和图6.19(b)中。参数t称为系统的时间常数,它控制着一阶系统响应的快慢。
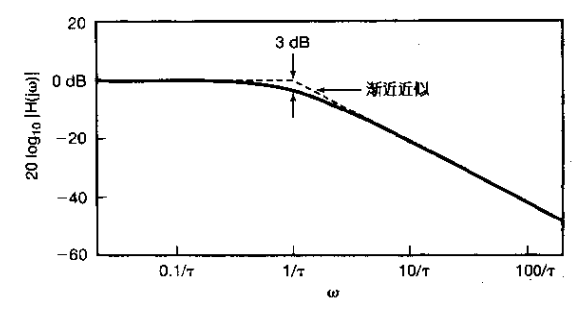
2、图6.20画出了式(6.22)频率响应的伯德图。这幅图体现了使用对数频率坐标的一个优点,这就是没有多大困难难就可以德奥一阶系统一个很有的近似伯德图。
为此,频率响应的对数特性,由式(6.22)可得
从该式可见,对于wt<<1,对数近似为零;而对于wt>>1,对数模就近似为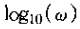
和
换句话说,一阶系统其对数模特性在第频和高频与的渐进线都是直线。低频渐进线[由式(6.26)给出]就是一条0dB线;而高频渐进线[由式(6.27)给出]相应于在|H(jw)|上每隔十倍频程有20dB的衰减,有事这就成为“没十倍频程20dB”渐进线。
注意由式(6.26)和式(6.27)所表示的这两条渐进线在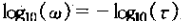
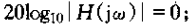
由于在w=1/t这一点,近似特性的斜率发生变化,因此这一点往往就称为转折频率。同时,由式(6.25)可知,在w=1/t这一点,式中对数内的两项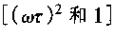
由于这个原因,w≥1/t这一点有时称为3dB点。
3、对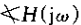
可以注意到这条近似特性作为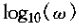
范围内是线性下降的(从0到-π/2),也就是说在转折频率上下各有一个十倍频程的范围内。同时,在w≥1/t时,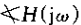
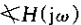
4、从上面的一阶系统可以再次看到时间和频率之间的相反关系。当t减小时,就就加速了系统的时间响应,即h(t)变得更向原点压缩阶跃响应的上升时间就减小了;榆次同时,转折率升高,即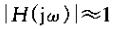
二)、二阶连续时间系统
1、二阶系统的线性常系数微分方程的一般形式为
其二阶系统的频率响应是
将H(jw)的分母因式化后,得
其中
若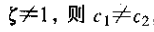
其中
由式(6.35),系统的单位冲激响应为
如果
此时的单位冲激响应为
参数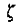
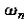
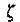
因此对于0<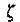
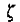
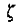
4、对于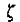
对于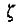
5、由式(6.33)可得
从这个表达式可以到处搞、第频率两条线性渐近线为
因此,对数模特性的低频渐近线是0dB线,而高频渐近线则有一个每隔十倍频程-40dB的斜率;也就是说,当w没增加10倍是,|H(jw)|就下降40dB。另外,两条渐近线在w=wn处相交。因此得出,对w≤wn,可以利用式(6.44)给出的近似,对对数模特性切得一个直线渐近线近似。为此,wn称为二阶系统的转折频率。
另外,也能求得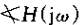
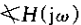
对
三)、有理型频率响应的伯德图
1、对于具有如下频率响应形式
和
的伯德图就能很快得到,因为
且
同时,对于系统函数为恒定增益的系统
因为,若K>0则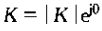
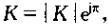
因为一个有理型频率夏官营可以按因式分解为一个恒定1增益和一阶、二阶项的乘积,所以它的伯德图就能由乘积中每一次昂的伯德图相加得到。
二、一阶与二阶离散时间系统
1、考虑由如下差分方程描述的一阶因果线性时不变系统
其中|a|<1.该系统的频率响应为
其单位脉冲为
同时,该系统的阶跃响应为
这么参数a的模|a|很类似于连续时间一阶系统中的时间常数t的作用,即|a|决定了一阶系统响应的速率。值得注意的事,与一阶连续时间系统不同,由式(6.51)索取定的一阶系统可以呈现出振荡的特性。这发生在a<0时,在这种情况下,阶跃响应即呈现出超量,又呈现出振荡特性。
2、由式(6.51)描述的一阶系统频率响应的模和相位分别是
和
当a>0时,系统呈现出高频衰减的特性,即|H(ejw)|在w接近-+π时的值比w接近0时的值小;二当a<0时,系统对高频分量较大,而对低频分量衰减。同时,也注意到,对于较小的|a|值,|H(ejw)|的最大值1/(1+a)和最小值1/(1-a)在数值上就逐渐靠近,因此|H(ejw)|的变化就相对平坦。另一方面,在|a|接近于1时,这两个值就相差很大,|H(ejw)|呈现出更为陡峭的峰值,这样就在一个较宽的频带内提供了具有良好选择性的滤波和放大。
二)、二阶离散时间系统
1、考虑一个二阶因果线性是不变系统,其差分方程为
其中0<r<1,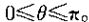
上式的分母可以因式分解,从而得
1)、当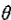
其中
这时系统的单位脉冲响应是
2)、当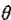
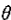
且
当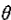
且
可看到,h[n]的衰减速率收r的控制,即r越接近1,h[n]衰减得越慢。类似的,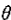
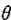
当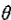
同时,对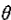
对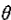
2、由式(6.57)给出的二阶系统就是相应连续时间系统前阻尼下的二阶系统,而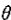
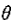
3、由式(6.59)定义的二阶系统具有复数系数因子(除非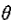
其中d1和d2都是实数,且|d1|和|d2|都小于1.式(6.70)就是下列差分方程的频率响应
在该情况下
其中
由此
这时两个衰减的实指数序列之和。同时
4、这一届仅仅福安心那些稳定的因果一阶和二阶系统,叶即频率响应是由定义的一阶和二阶系统。特别是,由式(6.51)定的因果系统,在|a|≥1时是不稳定的;同时,由式(6.56)定义的因果系统,在r≥1时也是不稳定的,而由式(6.71)定义的因果系统,在|d1|和|d2|中有一个超过1时也是不稳定的。