前言:
图由顶点集V(G)和边集E(G)组成,记为G=(V,E)。其中E(G)是边的有限集合,边是顶点的无序对(无向图)或有序对(有向图)。
思维导图:

一、基本概念:
1.定义
对有向图来说,E(G)是有向边(也称弧(Arc))的有限集合,弧是顶点的有序对,记为<v,w>,v、w是顶点,v为弧尾(箭头根部),w为弧头(箭头处)。
对无向图来说,E(G)是边的有限集合,边是顶点的无序对,记为(v, w)或者(w, v),并且(v, w)=(w,v)。
2、基本术语
顶点(Vertex):图中的数据元素。线性表中我们把数据元素叫元素,树中将数据元素叫结点。
顶点v的度:与v相关联的边的数目;
顶点v的出度:以v为起点有向边数;
顶点v的入度:以v为终点有向边数。
边:顶点之间的逻辑关系用边来表示,边集可以是空的。
无向边(Edge):若顶点V1到V2之间的边没有方向,则称这条边为无向边。
无向图(Undirected graphs):图中任意两个顶点之间的边都是无向边。(A,D)=(D,A)
有向边:若从顶点V1到V2的边有方向,则称这条边为有向边,也称弧(Arc)。用<V1,V2>表示,V1为狐尾(Tail),V2为弧头(Head)。(V1,V2)≠(V2,V1)。
有向图(Directed graphs):图中任意两个顶点之间的边都是有向边。
注意:无向边用“()”,而有向边用“< >”表示。
简单图:图中不存在顶点到其自身的边,且同一条边不重复出现。
无向完全图:无向图中,任意两个顶点之间都存在边。
有向完全图:有向图中,任意两个顶点之间都存在方向互为相反的两条弧。
权(Weight):与图的边或弧相关的数。
网(Network):带权的图。
子图(Subgraph):假设G=(V,{E})和G‘=(V',{E'}),如果V'包含于V且E'包含于E,则称G'为G的子图。
度(Degree):无向图中,与顶点V相关联的边的数目。 有向图中,入度表示指向自己的边的数目,出度表示指向其他边的数目,该顶点的度等于入度与出度的和。
简单路径:序列中顶点不重复出现的路径
简单回路:序列中第一个顶点和最后一个顶点相同的路径
路径的长度:一条路径上边或弧的数量。
连通图:图中任意两个顶点都是连通的。
极大连通子图:该子图是G连通子图,将G的任何不在该子图的顶点加入,子图将不再连通。
极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边,子图都将不再连通。
无向图G的极大连通子图称为G的连通分量。
有向图D的极大强连通子图称为D的强连通分量。
包含无向图G的所有顶点的极小连通子图称为G的生成树。
若T是G的生成树当且仅当T满足:T是G的连通子图、T包含G的所有顶点、T中无回路。
稀疏图:边很少的图。
稠密图:边很多的图。
二、图的存储结构
1.邻接矩阵法:
图的邻接矩阵存储方式是用两个数组来表示图;一个一维数组存储图中顶点信息,一个二维数组储存图中的边或弧的信息。
例如:
1.无向图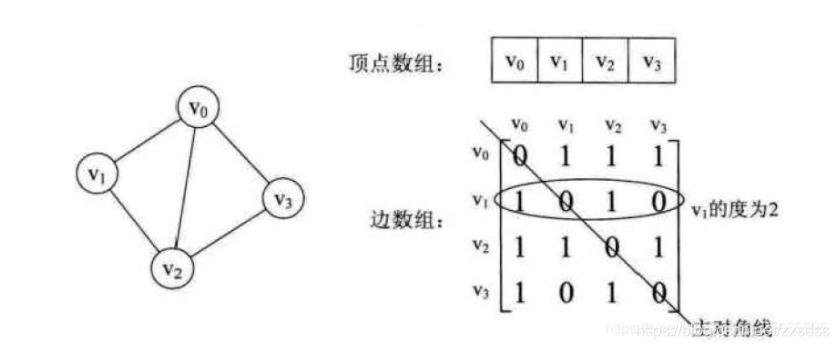
2.有向图: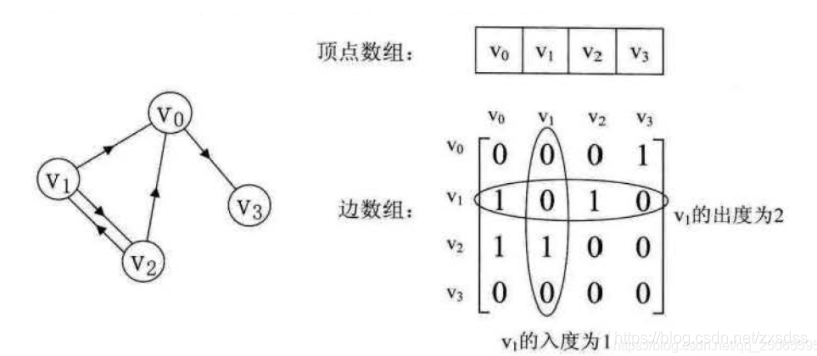
3.有向网图: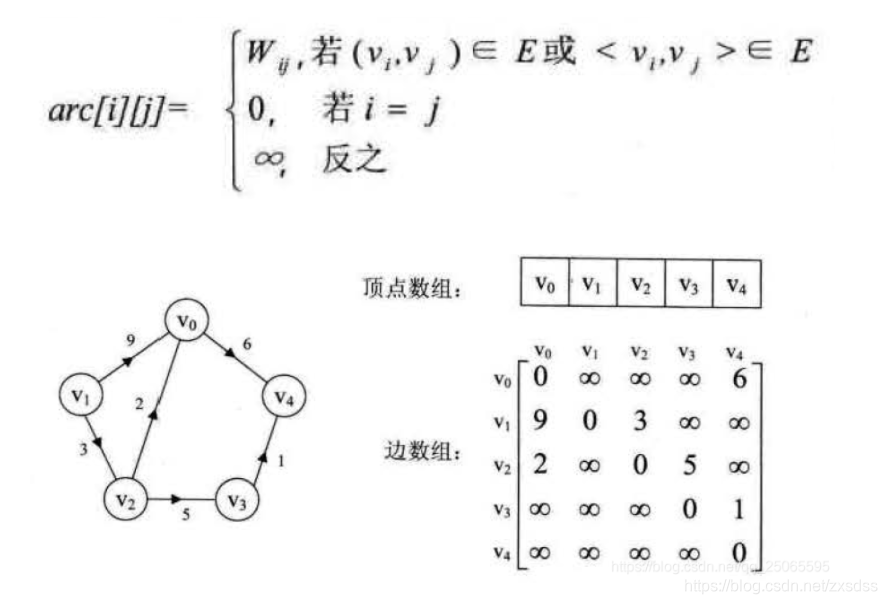
用邻接矩阵创建图:
typedef struct Graph{
char* vexs; //顶点
int** arcs; //边(使用**目的表示矩阵)
int vexNum;
int arcsNum;
}Graph;
//初始化一个图
Graph* initGraph(int vexNum)
{
Graph* G=(Graph*)malloc(sizeof(Graph));
G->vexs=(char*)malloc(sizeof(char) *vexNum);
G->arcs=(int**)malloc(sizeof(int*) *vexNum);
for(int i=0;i<vexNum;i++)
{
G->arcs[i]=(int*)malloc(sizeof(int) *vexNum);
}
G->vexNum=vexNum;
G->arcsNum=0;
return G;
}
//构建一个图
void createGraph(Graph* G,char* vexs,int* arcs)
{
for(int i=0;i<G->vexNum;i++)
{
G->vexs[i]=vexs[i];
for(int j=0;j<G->vexNum;j++)
{
/*
二维数组在内存中是连续存放的
所以,二维数组的赋值是个基于一维的
*/
G->arcs[i][j]=*(arcs+i*G->vexNum+j);
if(G->arcs[i][j]!=0)
{
G->arcsNum++;
}
}
}
/*
若为有向图:
G->arcsNum=G->arcsNum;
*/
G->arcsNum=G->arcsNum/2; //无向图
}2.邻接表法:
当一个图为稀疏图时,使用n*n的空间存储其邻接表显然比较浪费空间。而当前这种存储方法采取了顺序存储和链式存储相结合的方式,大大减少了不必要的浪费。
邻接表法简单来讲,首先见一个顺序表,将所有的顶点存至其中(顶点表)。而对于每个顶点A来讲采用链表结点的方式进行存储,将next指针指向其相邻接点a1→a2→a3…,这个单链表称为该顶点的边表(对于有向图则称为出边表)。故在此种存储方式中存在两种结点,一种是顶点表结点,一种是边表结点。
1.无向图:
2.有向图:需要用到邻接表和逆邻接表

3.带权值的网图(在边表结点定义中增加一个weight的数据域)
三、遍历图
1.深度优先遍历(DFS):从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。
2.广度优先遍历(BFS):类似于树的层次遍历。
四、最小生成树
最小生成树:构造连通网的最小代价生成树
最小生成树的两个算法都是基于MST性质:
假设(V,E)是一个连通图,U是顶点集V的一个非空子集,如果(u,v)
是一条具有最小权值的边,u属于U,v属于V-U,(u,v)必是最小生成树的边
1.prim算法(找点法)
算法简述:先将一个起点加入最小生成树,之后不断寻找与最小生成树相连的边权最小的边能通向的点,并将其加入最小生成树,直至所有顶点都在最小生成树中。


时间复杂度:O (V ^ 2)
known数组:存放已经使用过的顶点
dv数组:存放度数,随着添加的顶点,度数会随着发生变化
pv数组: 存放前继顶点
2.Kruskal算法(找边法):
算法简述:该算法可以叫做贪心算法。是连续地按照最小的权选择边,并且当所选的边不产生圈时就把它作为所取定的边。
注:
贪心算法(greedy algorithm,又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。

/*
kruskal找边法:
1.对边排序
2.选边
3.点与点的连线
核心问题:
1.建立一个边的数组并排序
2.判断图是否连通?
需要一个辅助数组,来去记录当前索引的节点所属于哪个连通分量
*/
typedef struct Edge{
int start; //起点索引
int end; //终点索引
int weight; //权值
}Edge;
Edge* initEdge(Graph* G)
{
int index=0;
Edge* edge=(Edge*)malloc(sizeof(Edge)*G->arcsNum);
for(int i=0;i<G->vexNum;i++)
{
for(int j=i+1;j<G->vexNum;j++)
{
if(G->arcs[i][j]!=MAX)
{
edge[index].start=i;
edge[index].end=j;
edge[index].weight=G->arcs[i][j];
index++;
}
}
}
return edge;
}
//排序权值函数(冒泡排序)
void sortEdge(Edge* edge,Graph* G)
{
Edge temp;
for(int i=0;i<G->arcsNum-1;i++)
{
for(int j=0;j<G->arcsNum-i-1;j++)
{
if(edge[j].weight>edge[j+1].weight)
{
temp=edge[j];
edge[j]=edge[j+1];
edge[j+1]=temp;
}
}
}
}
void kruskal(Graph* G)
{
//建立一个辅助数组
int* connected=(int*)malloc(sizeof(int)*G->vexNum);
for(int i=0;i<G->vexNum;i++)
{
connected[i]=i;
}
Edge* edge=initEdge(G);
sortEdge(edge,G);
for(int i=0;i<G->arcsNum;i++) //进行选边
{
int start=connected[edge[i].start];
int end=connected[edge[i].end];
if(start!=end) //判断是否围成一个圈
{
printf("v%c --> v%c = %d\n",G->vexs[edge[i].start],G->vexs[edge[i].end],edge[i].weight);
for(int j=0;j<G->vexNum;j++)
{
if(connected[j]==end)
{
connected[j]=start; //将每个节点的辅助值变成起点
}
}
}
}
}三、最小路径
Dijkstr算法:
求单源最短路径,即求一个顶点到任意顶点的最短路径,其时间复杂度为O(n*n)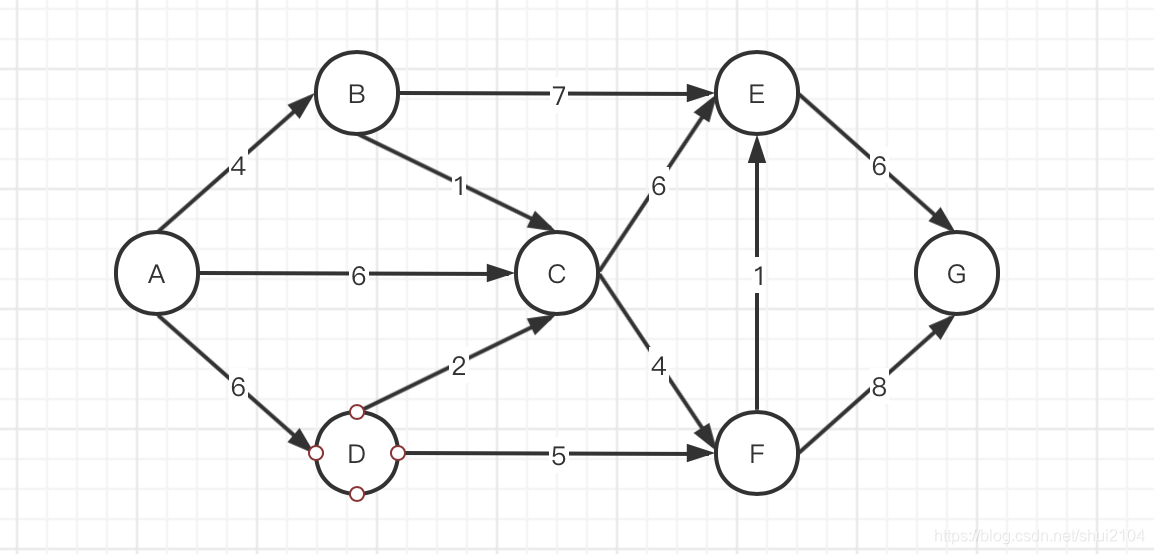
 S数组:存放已经使用过的顶点
S数组:存放已经使用过的顶点
U数组:未使用的过的顶点
A数组: 存放度数,随着添加的顶点,度数会随着发生变化
时间复杂度为:O(n^2)
注:由于学校并没有讲Floyd算法,所以不在这里呈现了。如果有需要,可在评论区下留言。
五、括扑排序
在了解这之前需了解两个概念:
DAG:有向无环图
AOV网:1.图的顶点表示任务
2.图的弧表示先后依赖关系
1.概念: 括扑排序就是将AOV中的顶点排成一个线性序列,
如果vi->vj有弧的话,那么vi就一定在vj前面
2.作用:判断图里是否有环(若打印的顶点数与图的顶点数相等,则说明图无环;反之即可)
3.括扑排序的流程:
1.找出没有前驱的顶点(入度为0),输出它,减掉 以它为出发点的所有边
2.重复第一步,直到图中不存在没有前驱的顶点
注:用一个栈存储入度为0的点,节省时间(以空间换时间)
六、关键路径


