GCN的基础理论

GCN的实用基础理论（编代码用）

1. 图的表示

$$\begin{array}{rl}& A：图结构的邻接矩阵\\ & \tilde{A}：有自连接的邻接矩阵\\ & \tilde{A}=A+I\\ & \tilde{D}：有自连接的邻接矩阵的度矩阵\\ & {\tilde{D}}_{ii}=\sum _j{\tilde{A}}_{ij}\\ & H：图节点的特征\\ & l:神经网络层数\end{array}$$

2. GCN的原理

$$H^{(l+1)}=\delta ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{(l)}{W}^{(l)})$$

• GCN的输入是邻接矩阵A和节点特征H，直接做内积，再乘一个参数矩阵W，然后激活一下，不就相当于一个的神经网络层？为什么要有自连接的邻接矩阵?
  提示：无法区分“自身节点”与“无连接节点”。只使用A的话，由于A的对角线上都是0，所以在和特征矩阵H相乘的时候，只会计算一个节点的所有邻居的特征的加权和，该节点本身的特征却被忽略了。

• 为什么需要有自连接的邻接矩阵的度矩阵？
  提示：A是没有经过归一化的矩阵，这样与特征矩阵H相乘会改变特征原本的分布，所以对A做一个标准化处理。平衡度很大的节点的重要性。（对称归一化拉普拉斯矩阵）
  $$Norm{A}_{ij}=\frac{A_{ij}}{\sqrt{d_i}\sqrt{d_j}}$$

3. GCN的底层实现（pytorch）

Pytorch-Geometric (PyG)：https://github.com/pyg-team/pytorch_geometric

官方文档 https://pytorch-geometric.readthedocs.io/en/latest/notes/introduction.html

PyG 提供了以下几个主要功能:

• Data Handling of Graphs（图数据处理）
• Common Benchmark Datasets（通用基准数据集）
• Mini-batches
• Data Transforms（数据转换）
• Learning Methods on Graphs（图学习算法）
• Exercises（训练）

3.1 Data Handling of Graphs（图数据处理）

图用于对对象（节点）之间的成对关系（边）进行建模。 PyG 中的单个图由torch_geometric.data.Data 的实例描述，该实例默认包含以下属性：

• data.x: 节点特征矩阵H，形状：[num_nodes, num_node_features]
• data.edge_index: 图邻接矩阵A，形状： [2, num_edges]，数据类型： torch.long

  举例：[[0,1,1,2],[1,0,2,1]]：表示0节点和1节点之间有边，1节点和2节点之间有边
  即：[[所有起点节点]，[所有终点节点]]。这里和一般思维不同，它们互为转置。注意使用时要转化为这种形式之后再使用

• data.edge_attr: 边特征矩阵，形状：[num_edges, num_edge_features]
• data.y: 训练目标(可以是任意形状)，e.g., 节点尺度上的标签，形状： [num_nodes, *] or 整张图尺度上的标签 [1, *]
• data.pos: 节点坐标矩阵，形状：[num_nodes, num_dimensions]

import torch
from torch_geometric.data import Data

# 注意：edge_index是定义所有边的源节点和目标节点的张量，不是索引元组的列表。
# --------------------第一种定义方法-----------------------------
edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)
x = torch.tensor([[-1], [0], [1]], dtype=torch.float)

data = Data(x=x, edge_index=edge_index)
>>> Data(edge_index=[2, 4], x=[3, 1])

# --------------------第二种定义方法-----------------------------
edge_index = torch.tensor([[0, 1],
                           [1, 0],
                           [1, 2],
                           [2, 1]], dtype=torch.long)
x = torch.tensor([[-1], [0], [1]], dtype=torch.float)

data = Data(x=x, edge_index=edge_index.t().contiguous()) # 注意这里edge_index进行了转置
>>> Data(edge_index=[2, 4], x=[3, 1])

3.2 Common Benchmark Datasets（通用基准数据集）

包含一些测试使用的基本数据集

3.3 Mini-batches

神经网络通常以批处理的方式训练。PyG 通过创建稀疏块对角邻接矩阵(由’ edge_index '定义)，并在节点维度上连接特征矩阵和目标矩阵来实现小批的并行化。

扫描二维码关注公众号，回复： 14870935 查看本文章

这种组合允许不同数量的节点和边在一个批次的例子（即A1~An它们的维度可以不同）：

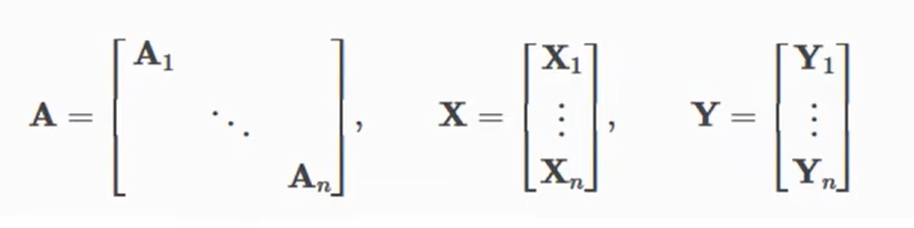
4. 实现GCN层

此公式可分为以下步骤:

1. 在邻接矩阵中添加自循环。
2. 线性变换节点特征矩阵。
3. 计算归一化系数。
4. 规范化节点特征
5. 对相邻节点特征求和(“add”聚合)。

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super().__init__(aggr='add')  # "Add" aggregation (Step 5).
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        # Step 1: 在邻接矩阵中添加自循环。~A
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: 线性变换节点特征矩阵。H*W
        x = self.lin(x)

        # Step 3: 计算归一化系数。
        row, col = edge_index # row：第一行数据，col：第二行数据
        deg = degree(col, x.size(0), dtype=x.dtype) # deg：度矩阵D; 参数为col算入度，参数为row算出度
        deg_inv_sqrt = deg.pow(-0.5) # D^(-0.5)
        deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
        # The result is saved in the tensor norm of shape [num_edges, ]
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # D^(-0.5) * ~A * D^(-0.5)

        # Step 4-5: 规范化节点特征，对相邻节点特征求和(“add”聚合)。
        return self.propagate(edge_index, x=x, norm=norm) # D^(-0.5) * ~A * D^(-0.5) * H * W

    def message(self, x_j, norm): # 扩展相乘，保证A和H能够相乘
        # x_j has shape [E, out_channels]

        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_j

5. GCN简单实例

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv

class GNN(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = GCNConv(dataset.num_node_features, 16) # 参数1: 节点特征数，参数2: 随机
        self.conv2 = GCNConv(16, dataset.num_classes) # 参数1: 与上一层一致，参数2: label类别数

    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        
        x = self.conv1(x, edge_index) # x为特征矩阵，edge_index为邻接矩阵
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)

from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='./data/Cora', name='Cora')

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = GNN().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

model.eval()
pred = model(data).argmax(dim=1)
correct = (pred[data.test_mask] == data.y[data.test_mask]).sum()
acc = int(correct) / int(data.test_mask.sum())
print(f'Accuracy: {
      
      acc:.4f}')

GCN的数学理论基础（理解用）

1. GCN基础

GNN公式： $H^{(l+1)}=f(A,H(l))$，其中$A$为图邻接矩阵，$H$为图上所有节点的特征矩阵

GCN公式：$H^{(l+1)}=\delta ({\hat{D}}^{-1/2}\hat{A}{\hat{D}}^{-1/2}{H}^{(l)}\theta )$，其中$D$为度矩阵，$\theta$为待学习的参数

GNN与GCN的区别：

GNN包含：

1. 从空域对图直接进行处理
2. 先将图从空域转化到谱域，然后再谱域操作完后，再转换到空域。即GCN。至于为什么要从空域转化到谱域再操作是因为在空域上由于图上的节点的结构并不固定（比如每个图上的节点的相邻节点都不一致），因此难以找到一个通用的卷积核对图进行提取特征，但转换到谱域上，就好处理了。这也是为什么要用到傅里叶变换的思想。

下面我们来探究以下GCN公式的来源。

2. 谱域图理论

谱域图理论简而言之就是研究与邻接矩阵A相关矩阵的一些性质的理论。

首先先复习一下线性代数中的几个相关概念：

（1）特征值和特征向量

对于一个矩阵A而言，如果$A\vec{x}=\lambda \vec{x}$，并且$|\vec{x}|\ne 0$，那么$\vec{x}$就是A的特征向量，$\lambda$则是对应的一个特征值

（2）实对称矩阵：矩阵的元素都为实数，并且矩阵是一个对称矩阵。

实对称矩阵的性质：实对称矩阵A的不同特征值对应的特征向量是正交的。写成数学表达式就是A可以表示为$A=U\Lambda U^T$，其中$U{U}^T=I$，$\Lambda$为一个对角线元素全为特征值，其他位置都为0的矩阵。

（3）半正定矩阵：

半正定矩阵的性质：矩阵是实对称矩阵；矩阵所有的特征值都大于等于0

（4）二次型：${\vec{x}}^{T}A\vec{x}$
（5）Rayleigh商：${\vec{x}}^{T}A\vec{x}/{\vec{x}}^T\vec{x}$。性质：当 $\vec{x}$ 是A的特征向量时，Rayleigh商即为对应的特征值。

有了上面这些理论，接下俩来看看与邻接矩阵A相关的一些矩阵：

拉普拉斯矩阵：$L=D-A$，$其中D为度矩阵$
对称规范化拉普拉斯矩阵： $L_{sym}=D^{-1/2}L{D}^{-1/2}$

为什么要研究上面这两个矩阵？是因为这两个矩阵具有优良的性质（这些性质能够应用到傅里叶变换上）。性质如下：

1. 这两个矩阵都是实对称矩阵（因此也是半正定矩阵），因此有n个大于等于零的特征值及对应的特征向量。
2. $L_{sym}$特征值的取值范围为[0,2]

第一个性质无需证明，因为上面已经给出矩阵的相关性质。下面来证明一下第二个性质：

1. 首先定义一个矩阵G，其中(i,i),（i,j)，(j,i)，(j,j)为1，其他位置为0，形式如下：
   $$\begin{array}{ccccccc}0& 0& 0& ...& 0& 0& 0\\ 0& 0& 0& ...& 0& 0& 0\\ 0& 0& 1& ...& 1& 0& 0\\ ...& & & & & & \\ 0& 0& 1& ...& 1& 0& 0\\ 0& 0& 0& ...& 0& 0& 0\\ 0& 0& 0& ...& 0& 0& 0\end{array}$$
2. 然后计算 ${\vec{x}}^{T}G\vec{x}$ ，其中$\vec{x}$为任意向量，结果为 $${\vec{x}}^{T}G\vec{x}=(x_i+x_j{)}^2$$（这里就不展开算了，自己可以在草稿纸上算一下）
3. 定义一个$L^{pos}=D+A$，易得 $$L^{pos}=D+A=\sum _{i,j\in E}G$$（后面这个求和公式就是所有情况的G矩阵相加）
4. 那么就能得到 ${\vec{x}}^T{L}^{pos}\vec{x}={\sum }_{i,j\in E}(x_i+x_j{)}^2$
5. 定义 $L_{sym}^{pos}=D^{-1/2}{L}^{pos}{D}^{-1/2}=D^{-1/2}(D+A)D^{-1/2}=I+D^{-1/2}A{D}^{-1/2}$。
6. 又因为 ${\vec{x}}^T{L}_{sym}^{pos}\vec{x}={\vec{x}}^T(I+D^{-1/2}A{D}^{-1/2})\vec{x}>=0$，因此展开变换后可以得到
   $${\vec{x}}^T{L}_{sym}\vec{x}/{\vec{x}}^T\vec{x}<=2$$
7. 发现等号左边是Rayleigh商，根据上面提到的Rayleigh商的性质，当 $\vec{x}$ 为矩阵的特征向量是，对应的Rayleigh商的值就是特征值，因此上式表达的就是 $L_{sym}$ 的所有特征值都小于等于2。
8. 又因为$L_{sym}$是半正定矩阵，因此特征值大于等于0。因此$L_{sym}$特征值的取值范围为[0,2]。

这个性质很重要，下面要用到。
下面我们来探讨一下图卷积用到的傅里叶变换的知识。

3. 傅里叶变换

首先什么是傅里叶变换？我们从下面的一张图来理解：

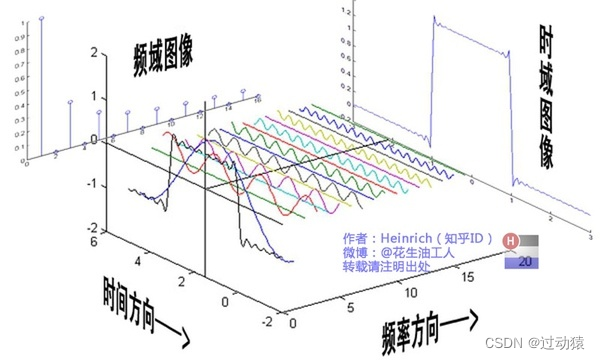
假设我们有一个描绘声波在时间上的函数$f(t)$，那么傅里叶变换的作用就是将这个函数分解成多个同样与时间作为自变量的正弦函数，原函数就是这些正弦函数的复合（至于为什么能变成多个正弦函数，这是傅里叶变换的数学原理，这里先不讨论），然后将这些函数放到以振幅为纵坐标，频率为横坐标的另一个坐标系上。简单来说，就是原函数是上面那个图的左视图（即时域图像），变换后的函数是上面那个图的右视图（即频域图像）。

为什么要做这样的变换呢？因为在有些任务中，我们如果在时域上去处理问题，会很麻烦，而在频域上去处理问题，会很简单。比如一男一女同时说话（众所周知，男生声音频率低，女生声音频率高），我们获得了这段音频，但是我们想去除这段音频中的男生的声音，如果仅根据时域图像来进行处理会非常麻烦，但是如果我们能将这段波映射到频域上，那么男生的声波都会集中在低频段，女生的声波都会集中在高频段，因此直接删除低频段的声波就能做到了，这是非常简单的。

反映到图上，我们在空域上很难解决问题，因此我们需要将这个问题换到另一个坐标系下去求解（即谱域），然后再把该结果转化回空域。这就是GCN中用到的傅里叶变换的思想。

说了这么多概念上的东西，下面来讲一下数学理论：

首先定义 $\vec{c}$ 为图中所有节点的某个特征向量，然后探讨一下 $L\vec{c}$ 的意义：

1. 首先 $L=D-A$，因此 $L\vec{c}=(D-A)\vec{c}=D\vec{c}-A\vec{c}$。
2. 然后分别计算 $D\vec{c}$ 和 $A\vec{c}$，之后做差，就能得到（右侧是个n*1的矩阵）
   $$L\vec{c}=\begin{array}{c}{\sum }_{x_j\in 与x_1相邻的节点}(x_1-x_j)\\ {\sum }_{x_j\in 与x_2相邻的节点}(x_2-x_j)\\ {\sum }_{x_j\in 与x_1相邻的节点}(x_1-x_j)\\ ...\\ {\sum }_{x_j\in 与x_1相邻的节点}(x_1-x_j)\end{array}$$
3. 我们看到矩阵右侧的每个元素，第一个元素是x1节点与所有和x1节点相邻的节点的差的求和，第二个元素是x2节点与所有和x2节点相邻的节点的差的求和，…，以此类推。因此 $L\vec{c}$ 是一个类似于聚合自己与邻居信息的操作，回想一下CNN，这不正是卷积核所做的工作嘛！！因此 $L\vec{c}$ 就是一个卷积操作，那么这和傅里叶变换有什么关系呢？
4. 因为L是一个实对称矩阵，因此 L可以表示为 $L=U\Lambda U^T$的形式，再把这个带入上面的 $L\vec{c}$ 中，得到$$L\vec{c}=U\Lambda U^T\vec{c}$$
5. 根据上面提到的实对称矩阵的性质可知，$U$和$U^T$都是正交矩阵，而我们知道一个向量（这里是$\vec{c}$）如果乘一个正交矩阵，就代表了这个向量映射到了另一个坐标空间中。（所以这里就用到了傅里叶变换的知识，将空域中的特征 $\vec{c}$ 映射到了谱域空间）
6. 那么 $L\vec{c}=U\Lambda U^T\vec{c}$ 的含义就是先将空域中的特征映射到谱域上（即$U^T\vec{c}$），然后在谱域上进行一定程度的变换（即$\Lambda U^T\vec{c}$），然后再将谱域中处理好的结果映射回空域上（即$U\Lambda U^T\vec{c}$）

到这里我们好像找到了图卷积公式的表达方法，那就是：
$$g_{\theta }\ast \vec{c}=U{g}_{\theta }(\Lambda )U^T\vec{c}$$

其中$g_{\theta }(\Lambda )$是关于$\Lambda$的多项式，$\theta$是其中要学习的参数。意义是在谱域空间对特征的一些变换提取。

但是我们不能忽略的是，这种方法我们首先需要分解$L$来得到$U$和$U^T$，这里的复杂度是$O(n^2)$，当图非常巨大时，计算的复杂度将无法承受。

因此如果选取一个比较好的$g_{\theta }(\Lambda )$从而避免分解 $L$ 就成为了一个比较必要的问题。

4. 图卷积

根据上面的分析我们已经得到了图卷积的计算公式，$$g_{\theta }\ast \vec{c}=U{g}_{\theta }(\Lambda )U^T\vec{c}$$

下面需要确定一个合适的$g_{\theta }(\Lambda )$来避免分解 $L$，普通的多项式$$a_{1}x+a_2{x}^2+...+a_n{x}^n$$其实也可以，但是在神经网络传播过程中容易造成梯度消失和梯度爆炸的问题。所以这里选择使用切比雪夫多项式。（这里看不懂可以先往下看）

切比雪夫多项式：
$$\begin{gathered} T_0(x)=1 \\ {T}_1(x)=x \\ {T}_{n+1}(x)=2x{T}_n(x)-T_{n-1}(x) \end{gathered}$$
切比雪夫多项式的性质：
$$T_n(cos\theta )=cosn\theta$$这就保证了不管n多大，在值域上都有一个摆动的稳定趋势，不会造成梯度消失或爆炸的问题。

但这又引入了一个新问题，自变量的定义域为[-1,1]，因此这里就用到了上面提到的：$L_{sym}$特征值的取值范围为[0,2]，这条结论。

因此我们可以将 $L_{sym}-I$ 作为最终决定的实对称矩阵，将它作为切比雪夫多项式的输入，他的特征值的取值范围正好是[-1,1]。（至于为什么要把 $L_{sym}-I$ 当作输入，除了他能防止梯度消失或爆炸，最重要的是他是一个实对称矩阵，以它作为输入能避免分解 $L$ 的问题（这也是我们的核心问题），下面会讲到为什么它可以避免分解 $L$）

因此，我们最终决定$$g_{\theta }(\Lambda )=\sum _{k=0}^K{\theta }_k{T}_k(\Lambda )$$

接下来，我们将卷积公式进行展开：$$g_{\theta }\ast \vec{c}=U\sum _{k=0}^K{\theta }_k{T}_k(\Lambda )U^T\vec{c}$$

$$g_{\theta }\ast \vec{c}=\sum _{k=0}^K{\theta }_k(U{T}_k(\Lambda )U^T)\vec{c}$$
然后由于 $U{T}_k(\Lambda )U^T=T_k(U\Lambda U^T)$（这一点可以自己展开去证明一下，这里就不证明了）

$$g_{\theta }\ast \vec{c}=\sum _{k=0}^K{\theta }_k{T}_k(U\Lambda U^T)\vec{c}$$

$$g_{\theta }\ast \vec{c}=\sum _{k=0}^K{\theta }_k{T}_k(U\Lambda U^T)\vec{c}$$

这里我们看到切比雪夫多项式的输入是$U\Lambda U^T$，这就要保证输入的矩阵必须是一个实对称矩阵，而上面我们提到了，我们要将$L_{sym}-I$作为切比雪夫多项式的输入，而$L_{sym}-I$的确就是一个实对称矩阵。所以代入，公式就变为：

$$g_{\theta }\ast \vec{c}=\sum _{k=0}^K{\theta }_k{T}_k(L_{sym}-I)\vec{c}$$

到此，我们发现，$U$和$U^T$已经消失了，即不需要分解 $L$ 来求这两个矩阵了，我们解决了最开始提到的核心问题。接下来，我们再对这个公式进行化简，看最终会变成一个什么形式。

为了简化这个问题，我们令K=1，即只取切比雪夫多项式的前两个，$T_0(x)=1$和$T_1(x)=x$，展开求和公式得到

$$g_{\theta }\ast \vec{c}={\theta }_0{T}_0(L_{sym}-I)\vec{c}+{\theta }_1{T}_1(L_{sym}-I)\vec{c}$$

$$g_{\theta }\ast \vec{c}={\theta }_0\vec{c}+{\theta }_1(L_{sym}-I)\vec{c}$$

由于$L_{sym}=D^{-1/2}L{D}^{-1/2}=D^{-1/2}(D-A)D^{-1/2}=I-D^{-1/2}A{D}^{-1/2}$

代入得：

$$g_{\theta }\ast \vec{c}={\theta }_0\vec{c}-{\theta }_1{D}^{-1/2}A{D}^{-1/2}\vec{c}$$

为了进一步简化问题，我们令${\theta }_1=-{\theta }_0$，那么公式变为：

$$g_{\theta }\ast \vec{c}={\theta }_0(I+D^{-1/2}A{D}^{-1/2})\vec{c}$$

再简化一下问题，直接将 $I+D^{-1/2}A{D}^{-1/2}$ 转化为 $D^{-1/2}\hat{A}{D}^{-1/2}$ ，其中 $\hat{A}=A+I$

（至于为什么，是因为先加上单位矩阵再归一化是有一定的图意义的，即给每个节点加上了自环，这样与 $\vec{c}$ 相乘后结果就会保留自身节点的特征信息，而不仅仅是该节点与其相邻节点的特征值差的总和，如果还不太懂就可以去看看https://zhuanlan.zhihu.com/p/107162772）

这样公式就变为了：

$$g_{\theta }\ast \vec{c}=D^{-1/2}\hat{A}{D}^{-1/2}\vec{c}{\theta }_0$$

把这个公式和我们最开始提到的那个GCN的公式来对比一下：
$$H^{(l+1)}=\delta ({\hat{D}}^{-1/2}\hat{A}{\hat{D}}^{-1/2}{H}^{(l)}\theta )$$

发现这两个公式在形式上完全一致，所以这个公式就是我们最开始给出的公式的来源。
到此，数学推理完毕。