1.线性回归的基本概念
在回归分析中,如果只包含一个自变量和一个因变量,且二者关心可近似用一条直线表示,则称该回归分析为一元线性回归分析。如果包含两个及两个以上的自变量,且因变量与自变量之间是线性关系,则称该回归分析为多元线性回归分析。
2.线性回归算法
设预测函数(目标函数)为:
hθ(x) = θ0 + θ1x1 + θ2x2 + θ3x3 + θ4x4
为了符号表示更方便,去x0=1,得到预测函数如下:
hθ(x) = θ0x0 + θ1x1 + θ2x2 + θ3x3 + θ4x4
将hθ(x)转为向量表示:
令列向量 x = [x0;x1;x2;x3;x4]
令列向量 θ = [θ0;θ1;θ2;θ3;θ4]
则hθ(x) = θTx
即:hθ(x) = θ0x0 + θ1x1 + θ2x2 + θ3x3 + θ4x4 = θTx (x0=1)
3.多元梯度下降算法
预测函数(目标函数): hθ(x) = θTx = θ0x0 + θ1x1 + θ2x2 + …+ θnxn (x0=1)
参数: θ0,θ1,θ2,…,θn
代价函数:
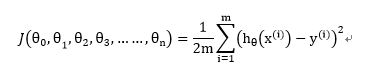
我们应该清楚针对多元线性回归,上面代价函数中的θ和x(i)都是n+1维向量。
梯度下降算法:
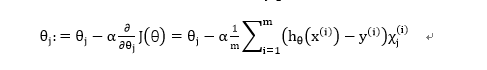
一定要同步更新θj,其中 j = 0,1,2,…n。
循环迭代,直至收敛,即可求得θj,按照此法求出所有的参数θ0,θ1,θ2,…,θn。
4.总结
对于很多现实中的数据,我们通过线性回归也许不能很好的将其与训练样本数据进行拟合,我们可能需要非线性回归得到更好的拟合。这种情况我们可以通过合理的更换特征要素,进而将非线性回归转为线性回归。