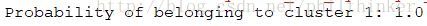OS: Windows 10 x64
Python: Anaconda 4.4.0 (Python 2.7)
IDE: Spyder
Thanks Cameron Davidson-Pilon for his great work of Bayesian Methods for Hackers: Probabilistic Programming and Bayesian Inference.
接上一篇:
用Python实现概率编程与贝叶斯推断 - Part I - Hello PyMC
贝叶斯景象图
对于一个含有
import scipy.stats as stats
from matplotlib import pyplot as plt
from IPython.core.pylabtools import figsize
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
figsize(14 , 6)
fig = plt.figure()
plt.subplot(121 )
x = y = np.linspace(0 , 5 , 100 )
X, Y = np.meshgrid(x, y)
jet = plt.cm.jet
exp_x = stats.expon.pdf(x, scale=3 )
exp_y = stats.expon.pdf(x, scale=10 )
M = np.dot(exp_x[:, None ], exp_y[None , :])
CS = plt.contour(X, Y, M)
im = plt.imshow(M, interpolation= 'none' , origin= 'lower' ,
cmap= jet, extent= (0 , 5 , 0 , 5 ))
ax = fig.add_subplot(122 , projection= '3d' )
ax.plot_surface(X, Y, M, cmap= jet)
ax.view_init(azim=390 )
ax.set_xlabel('Value of $p_1$' )
ax.set_ylabel('Value of $p_2$' )
ax.set_zlabel('Density' )运行结果如下:
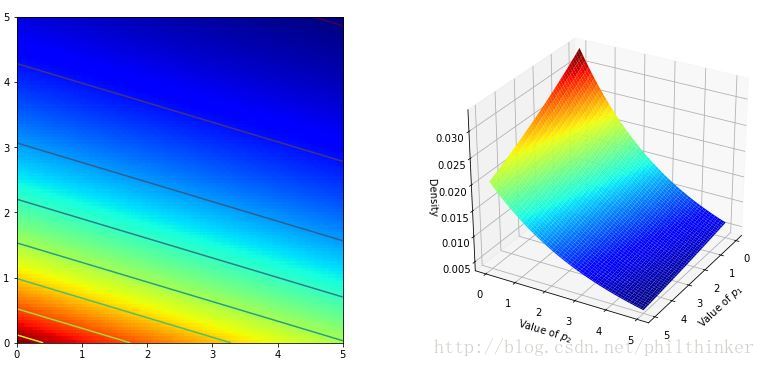
观测样本会影响概率面的形状,在某些局部产生拉伸或者挤压,以表明参数对的真实值在哪里。最后得到的是后延分布的形状。注意:如果某一点处先验概率是0,那么在这一点推不出后验概率。
MCMC算法
概述
要想得到后验分布上的“山峰”,我们需要对整个后验概率空间进行搜索。MCMC的背后思想是如何聪明地对空间进行搜索。MCMC的返回值是后验分布的一些样本点,而非分布本身。这些返回的样本被称之为“迹”。MCMC的搜索位置能收敛到后延概率最高的区域,即朝着概率值增加的方向前进。
MCMC可由一系列算法实现,这些算法大多可以描述为以下几步:
- 从当前位置开始。
- 尝试移动一个位置。
- 根据新位置是否服从于该概率数据和先验分布,来决定是否采纳这次移动。
- 如果采纳,就在新位置重复第1步;如果不采纳,那么留在原处并重复第1步。
- 大量迭代之后返回所有被采纳的点。
除了MCMC之外,寻找后验概率还可通过拉普拉斯近似、变分贝叶斯等方法。
实例:聚类
首先初始化一组数据:
# Raw data
# True parameters
mu1_true = 120.0
mu2_true = 200.0
tau1_true = 0.001
tau2_true = 0.009
data1 = pm.rnormal(mu1_true, tau1_true, size=1000)
data2 = pm.rnormal(mu2_true, tau2_true, size=800)
data = np.append(data1,data2)
# Save to npy/npz files
np.savez("rnormal_datas",data,data1,data2,mu1=mu1_true,mu2=mu2_true,
tau1=tau1_true, tau2=tau2_true)
figsize(12,4)
plt.hist(data, bins=10,color="k", histtype="stepfilled", alpha=0.8)
plt.ylim([0, None])
plt.xlabel("Value")
plt.ylabel("Count")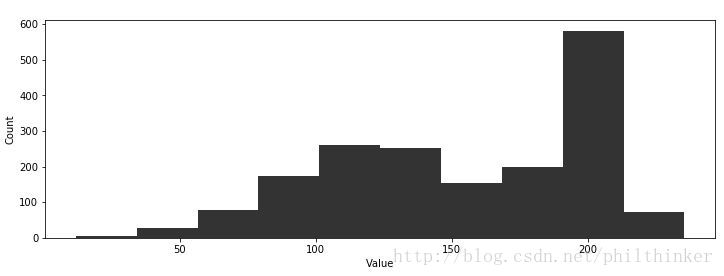
现在我们对其进行估计,我们并不知道这一组数据来自两个正态分布,且两个分布的样本点数量不一致。但是我们可以通过观察图像大致猜出数据集中包含两个正态分布,也可以大致估计其参数。可见,需要估计的参数包含:
- 样本点所属分布1和2的概率:
p ,1−p 。 - 两个正态分布的参数:
μ1 ,μ2 ,σ1 ,σ2 。注意:τ=1σ2
下面开始设定先验概率:
# Prior
p = pm.Uniform("p", 0.0, 1.0)
# Select cluster for the data
assignment = pm.Categorical("assignment",[p, 1-p], size=data.shape[0])
taus = 1.0/pm.Uniform("stds",0,16, size=2)**2 # Prior
centers = pm.Normal("centers", [125,210],[0.01,0.01],size=2)这里为
分配每个点所处的聚类簇:
@pm.deterministic
def center_i(assignment=assignment, centers=centers):
return centers[assignment]
@pm.deterministic
def tau_i(assignment=assignment, taus=taus):
return taus[assignment]由于我们事先已经利用 Categorical 为每个点选好了初始的聚类簇,这一步仅是将每个聚类簇对应的先验分布的参数赋给每个样本点,因此不具有随机性,使用确定变量。
结合样本点数据:
observations = pm.Normal("obs", center_i, tau_i,value=data, observed=True)注意此时 observations 变量的值与 data 完全相同,但是其每个值都被赋予了一个 center 属性和一个 tau 属性。
生成 PyMC 模型:
model = pm.Model([p, assignment, taus, centers])执行 MCMC 空间探索法:
mcmc = pm.MCMC(model)
mcmc.sample(50000)sample方法的参数决定执行步数。
MCMC的执行需要一段时间,完成后可以利用其 trace 方法查看它的“迹”。
figsize(12 , 6 )
plt.subplot(311)
line_width = 1
center_trace = mcmc.trace("centers" )[:]
colors = ["#348ABD" , "#A60628" ]
plt.plot(center_trace[:,0], label= "trace of center 0" ,
c= colors[0], lw= line_width)
plt.plot(center_trace[:,1], label= "trace of center 1" ,
c= colors[1], lw= line_width)
plt.title("Traces of unknown parameters" )
leg = plt.legend(loc= "upper right" )
leg.get_frame().set_alpha(0.7 )
plt.subplot(312)
std_trace = mcmc.trace("stds" )[:]
plt.plot(std_trace[:,0], label= "trace of std of cluster 0" ,
c= colors[0], lw= line_width)
plt.plot(std_trace[:,1], label= "trace of std of cluster 1" ,
c= colors[1], lw= line_width)
plt.legend(loc= "upper left" )
plt.subplot(313)
p_trace = mcmc.trace("p" )[:]
plt.plot(p_trace, label= "$p$: frequency of assignment to cluster 0" ,
color= "#467821" , lw= line_width)
plt.xlabel("Steps")
plt.ylim(0 , 1)
plt.ylabel('Value')
plt.legend();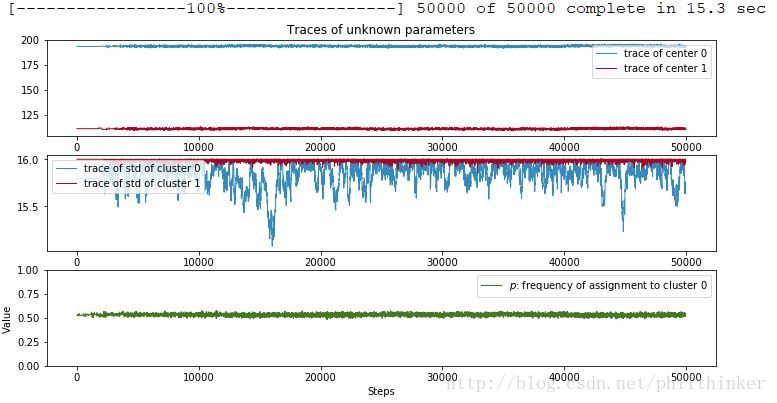
注意这些迹并非收敛到一点,而是收敛到满足一定分布下,概率较大的点集。最初的点与目标关系不大,可以丢弃,产生这些可丢弃点的过程称为预热期。这些迹总是在基于之前的位置移动。
我们可以重启MCMC采用,但这并不会重复整个过程,因为已走到的位置被隐式地存在value属性中。
mcmc.sample(100000)
figsize(15, 8)
line_width = 1
center_trace = mcmc.trace("centers")[:]
std_trace = mcmc.trace("stds")[:]
colors = ["#348ABD" , "#A60628"]
plt.plot(center_trace[:,0], label= "trace of center 0",
c=colors[0], lw=line_width)
plt.plot(center_trace[:,1], label= "trace of center 1",
c=colors[1], lw=line_width)
leg = plt.legend(loc= "upper right" )
leg.get_frame().set_alpha(0.7)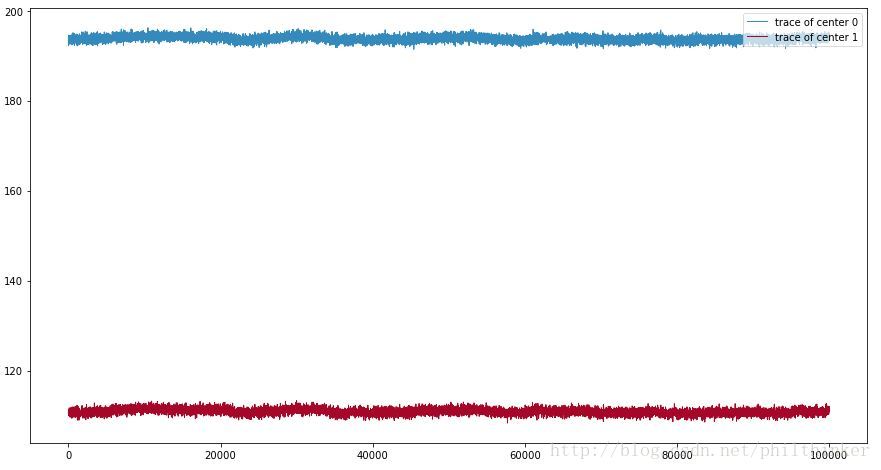
使用MCMC实例的trace方法时,可以通过传入参数chain来索引想要返回哪一次的sample调用结果,默认情况下chain=-1,即最后一次调用结果。
此时我们已经估计了各个未知元素的后验概率分布了,我们的目标的聚类。下面我们根据MCMC执行结果绘图:
figsize(11.0 , 4)
std_trace = mcmc.trace("stds")[:]
_i = [1 , 2 , 3 , 4]
for i in range (2):
plt.subplot(2 , 2 , _i[2*i])
plt.title("Posterior distribution of center of cluster %d " %i)
plt.hist(center_trace[:, i], color= colors[i], bins=30,
histtype= "stepfilled" )
plt.subplot(2 , 2 , _i[2*i+1])
plt.title("Posterior distribution of standard deviation of cluster %d " %i)
plt.hist(std_trace[:, i], color=colors[i], bins=30,
histtype= "stepfilled" )
plt.ylabel('Density' )
plt.xlabel('Value' )
plt.tight_layout()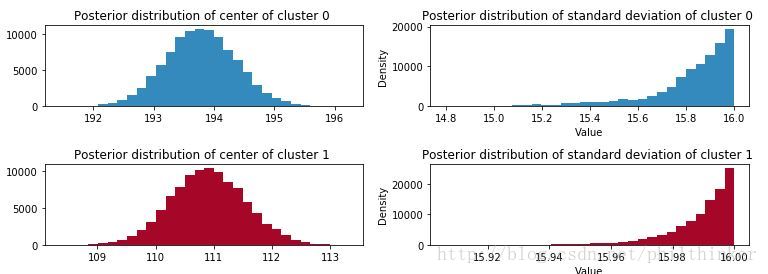
我们得到了关于正态分布各个参数的分布,下一步我们考虑如何选择能够满足最佳匹配参数。一个简单的方法是选择后验分布的均值。
import scipy.stats as stats
norm = stats.norm
x = np.linspace(20 , 300 , 500)
posterior_center_means = center_trace.mean(axis=0)
posterior_std_means = std_trace.mean(axis=0)
posterior_p_mean = mcmc.trace("p" )[:].mean()
plt.hist(data, bins=20 , histtype= "step" , normed= True , color= "k" ,
lw=2 , label= "histogram of data" )
y = posterior_p_mean*norm.pdf(x, loc= posterior_center_means[0],
scale= posterior_std_means[0])
plt.plot(x, y, label="cluster 0 (using posterior-mean parameters)",lw=3)
plt.fill_between(x, y, color= colors[1], alpha=0.3)
y = (1 - posterior_p_mean)*norm.pdf(x,loc= posterior_center_means[1],
scale= posterior_std_means[1])
plt.plot(x, y, label= "cluster 1 (using posterior-mean parameters)" , lw=3 )
plt.fill_between(x, y, color= colors[0], alpha=0.3)
plt.legend(loc= "upper left" )
plt.title("Visualizing clusters using posterior-mean parameters" )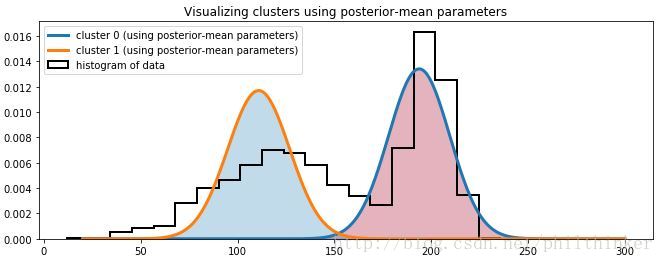
回到聚类问题上,我们的目标是得到观测数据所属的类别为1的概率值。计算方法可根据贝叶斯原理。
norm_pdf = stats.norm.pdf
p_trace = mcmc.trace("p" )[:]
x = 175
v = p_trace * norm_pdf(x, loc= center_trace[:, 0],
scale= std_trace[:, 0 ]) > \
(1 - p_trace)*norm_pdf(x, loc= center_trace[:, 1],
scale= std_trace[:, 1])
print "Probability of belonging to cluster 1:" , v.mean()改进收敛性
理想情况下,我们希望起始位置就在分布图形的山峰处,因为这其实是后验概率所处的区域。我们将山峰位置称为最大后验,简称MAP。当然MAP的真实位置是未知的,PyMC提供了一个估计该位置的对象,它接受一个PyMC model对象作为初始化参数,并提供fit()方法将model对象的变量值都置为其MAP估计值。
map_=pm.MAP(model)
map_.fit()MAP优化方法也可以认为指定,默认情况下使用的是SciPy的fmin算法。还可以选择使用Powell方法:
map_.fit(method='fmin_powell')即使在执行 mcmc.sample 之前以MAP为初值,最好也准备一段预热期。调用sample时通过指定参数burn来让sample丢弃前 n 个样本。如:
model = pm.Model([p, assignment, taus, centers])
map_=pm.MAP(model)
map_.fit()
mcmc = pm.MCMC(model)
mcmc.sample(100000, 50000)自相关性
自相关性用来衡量一串数字与自身的相关程度,1表示完美正相关,0表示完全无关,-1表示完美负相关。一种理解相关性的方式是问:如果我处于一个序列在
举个例子:
figsize(12.5 , 4)
x_t = pm.rnormal(0 , 1 , 200)
x_t[0] = 0
y_t = np.zeros(200)
for i in range (1 , 200):
y_t[i] = pm.rnormal(y_t[i - 1], 1)
plt.plot(y_t, label= "$y_t$" , lw=3)
plt.plot(x_t, label= "$x_t$" , lw=3)
plt.xlabel("Time, $t$")
plt.ylabel('Value')
plt.title("Two different series of random values")
plt.legend();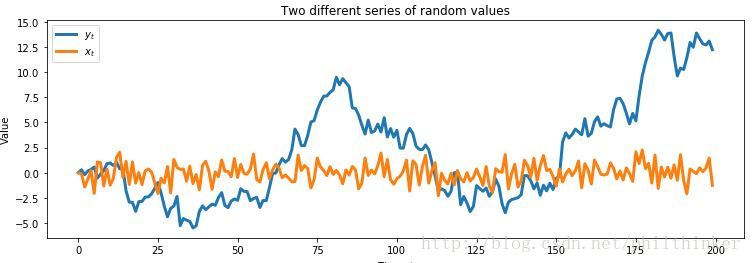
上图
def autocorr (x):
result = np. correlate(x, x, mode= 'full' )
result = result / np. max(result)
return result[result. size / 2 :]
colors = ["#348ABD" , "#A60628" , "#7A68A6" ]
x = np.arange(1 , 200)
plt.bar(x, autocorr(y_t)[1 :], width=1 , label= "$y_t$" ,
edgecolor = colors[0], color = colors[0])
plt.bar(x, autocorr(x_t)[1 :], width=1 , label= "$x_t$" ,
color= colors[1], edgecolor= colors[1])
plt.legend(title= "autocorrelation" )
plt.ylabel("Measured correlation \n between $y_t$ and $y_{t-k}$." )
plt.xlabel("$k$ (lag)" )
plt.title("Autocorrelation plot of $y_t$ and $x_t$ for differing\
$k$ lags" );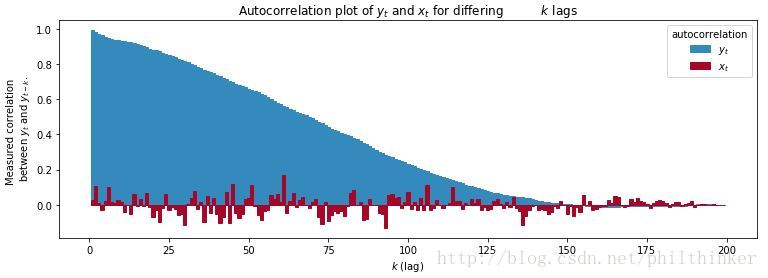
从上图可以看出随着间隔
MCMC算法会天然地返回具有相关性的采样结果。如果一次采样过程的探索效果很好,那么表现出的自相关性也会很高。
如果后验样本的自相关性很高,又会引起另一个问题:很多后处理算法需要样本间彼此独立。这个问题可以通过每隔
Matplot
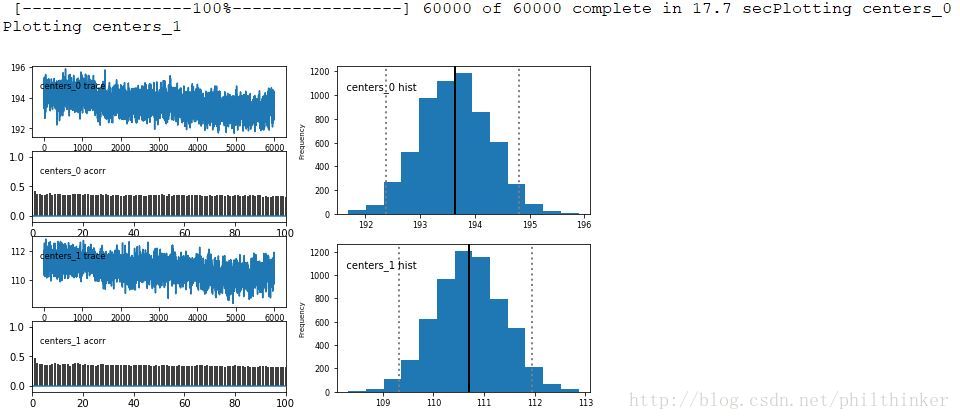
PyMC提供了一种简单的方法绘制直方图、自相关图和迹图——Matplot。Matplot包含一个plot方法,以MCMC对象为参数,返回每个变量(最多10个)的后验分布、迹和自相关函数。
from pymc.Matplot import plot as mcplt
mcmc.sample(60000, 0, 10)
mcplt(mcmc.trace("centers", 2), common_scale=False)下一篇:
用Python实现概率编程与贝叶斯推断 - Part III - 大数定律(未完待续……)