协方差,方差,标准差,均方差
方差Variance
记法:D(X)
X为随机变量
D ( X ) = E ( X 2 ) − E 2 ( X ) D(X) = E(X^{2})-E^{2}(X) D(X)=E(X2)−E2(X), 平方的均值减去均值的平方
推导过程:
E ( X ) = Σ ( x i . p i ) = X ˉ E(X) = \Sigma (x_{i}.p_{i}) =\bar X E(X)=Σ(xi.pi)=Xˉ, 则这里的 X ˉ \bar X Xˉ就是一个常数了, E 2 ( X ) = X ˉ 2 E^{2}(X)=\bar X^{2} E2(X)=Xˉ2
D ( X ) = E [ ( X − E ( X ) ) 2 ] = E [ ( X − X ˉ ) 2 ] = E [ X 2 + X ˉ 2 − 2 X ˉ X ] = E ( X 2 ) + X ˉ 2 − 2 X ˉ E ( X ) = E ( X 2 ) − E 2 ( X ) D(X)=E[(X-E(X))^{2}] = E[(X-\bar X)^{2}]=E[X^{2}+\bar X^{2}-2\bar XX]=E(X^{2})+\bar X^{2}-2\bar XE(X)= E(X^{2})-E^{2}(X) D(X)=E[(X−E(X))2]=E[(X−Xˉ)2]=E[X2+Xˉ2−2XˉX]=E(X2)+Xˉ2−2XˉE(X)=E(X2)−E2(X)
方差的性质:
- 设 C C C为常数,则 D ( C ) = 0 D(C)=0 D(C)=0
- D ( c x ) = c 2 D ( x ) D(cx) = c^{2}D(x) D(cx)=c2D(x)
- D ( − x ) = D ( x ) , D ( − 2 x ) = 4 D ( x ) D(-x) = D(x), D(-2x)=4D(x) D(−x)=D(x),D(−2x)=4D(x)
标准差(Standard Deviation),也叫 均方差
记为: σ X = D X \sigma X = \sqrt{DX} σX=DX
协方差Covariance
设有随机变量 X , Y X, Y X,Y,称 E [ ( X − E X ) ( Y − E Y ) ] E[(X -EX)(Y-EY)] E[(X−EX)(Y−EY)] 为随机变量 X , Y X, Y X,Y 的协方差,记为 C O V ( X , Y ) COV(X,Y) COV(X,Y). 即有: C O V ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] COV(X,Y) = E[(X-E(X))(Y-E(Y))] COV(X,Y)=E[(X−E(X))(Y−E(Y))]
协方差用来衡量两个变量的总体误差,这和只表示一个变量误差的方差不同,如果两个变量的变化趋势一致,也就是说,如果其中一个大于自身的期望值,另一个也大于自身的期望值,则两个变量之间的协方差就是正值。如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,则两个变量之间的协方差就是负值。
协方差和方差的关系:
C O V ( X , X ) = D ( X ) COV(X,X) = D(X) COV(X,X)=D(X)
而方差是协方差的一种特殊情况,即当两个变量是相同的情况下
协方差和相关系数的关系:
相关系数: ρ X , Y = C O V ( X , Y ) D X D Y , ρ X , Y \rho_{X,Y}=\frac{COV(X,Y)}{\sqrt{DX}\sqrt{DY}},\quad\quad \rho_{X,Y} ρX,Y=DXDYCOV(X,Y),ρX,Y是一个无量纲的量
统计学中的方差和协方差的定义
在统计学中,方差是用来度量单个随机变量的离散程度,而协方差则一般用来刻画两个随机变量的相似程度,其中,
方差的计算公式为:
σ x 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 \sigma_{x}^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar x)^{2} σx2=n−11i=1∑n(xi−xˉ)2
在此基础上,协方差的计算公式被定义为:
σ ( x , y ) = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) \sigma(x,y)=\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar x)(y_{i}-\bar y) σ(x,y)=n−11i=1∑n(xi−xˉ)(yi−yˉ)
上式中,符号 x ˉ , y ˉ \bar x, \bar y xˉ,yˉ 分别表示量随机变量所对应的观测样本均值,据此,我们发现:方差 σ x 2 \sigma_{x}^{2} σx2 可视作随机变量 x x x 关于其自身的协方差 σ ( x , x ) \sigma(x,x) σ(x,x)
从方差/协方差到协方差矩阵
根据方差的定义,给定d个随机变量 x k ∈ R n , k = 1 , 2 , 3 , . . . , d x_{k}\in \mathbb{R^{n}},k=1,2,3,...,d xk∈Rn,k=1,2,3,...,d,则这些随机变量的方差为:
这里设随机变量的个数为 d d d,可以看作机器学习中的数据矩阵 X n × d X_{n\times d} Xn×d, 即n个样本,每个样本有 d 个特征,每个特征就是一个随机变量,即每一列就是一个随机变量。 x ˉ k \bar x_{k} xˉk就表示的是每一列的均值。
σ ( x k , x k ) = 1 n − 1 ∑ i = 1 n ( x k , i − x ˉ k ) 2 , k = 1 , 2 , 3... , d \sigma(x_{k},x_{k})=\frac{1}{n-1}\sum_{i=1}^{n}(x_{k,i}-\bar x_{k})^{2},\quad k=1,2,3...,d σ(xk,xk)=n−11i=1∑n(xk,i−xˉk)2,k=1,2,3...,d
其中, x k , i x_{k,i} xk,i表示随机变量 x k x_{k} xk中的第 i i i 个观测样本, n n n 表示样本量,每个随机变量所对应的观测样本数量均为 n n n 。
对于这些随机变量,我们还可以根据协方差的定义,求出两两之间的协方差,即:
σ ( x m , x k ) = 1 n − 1 ∑ i = 1 n ( x m , i − x ˉ m ) ( x k , i − x ˉ k ) \sigma(x_{m},x_{k})=\frac{1}{n-1}\sum_{i=1}^{n}(x_{m,i}-\bar x_{m})(x_{k,i}-\bar x_{k}) σ(xm,xk)=n−11i=1∑n(xm,i−xˉm)(xk,i−xˉk)
因此,协方差矩阵为:
Σ = [ σ ( x 1 , x 1 ) ⋯ σ ( x 1 , x d ) ⋮ ⋱ ⋮ σ ( x d , x 1 ) ⋯ σ ( x d , x d ) ] ∈ R d × d \Sigma=\left[\begin{array}{ccc} \sigma\left(x_{1}, x_{1}\right) & \cdots & \sigma\left(x_{1}, x_{d}\right) \\ \vdots & \ddots & \vdots \\ \sigma\left(x_{d}, x_{1}\right) & \cdots & \sigma\left(x_{d}, x_{d}\right) \end{array}\right] \in \mathbb{R}^{d \times d} Σ=⎣⎢⎡σ(x1,x1)⋮σ(xd,x1)⋯⋱⋯σ(x1,xd)⋮σ(xd,xd)⎦⎥⎤∈Rd×d
其中,对角线上的元素为各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差,根据协方差的定义,我们可以认定:矩阵 Σ \Sigma Σ为对称矩阵(symmetric matrix),其大小为 d × d d\times d d×d。
之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。
协方差矩阵的计算
协方差矩阵的定义1: X n × d X_{n\times d} Xn×d行表示样本,列表示特征(也叫随机变量)
矩阵中的数据按行排列与按列排列求出的协方差矩阵是不同的,这里方法①的数据是按行排列的,就是每一行表示一个样本,而每一列表示一个特征,或者每一列也叫一个随机变量。
step1:找出随机变量 c i c_{i} ci
X n × d = [ x 1 T x 2 T ⋮ x n T ] = [ x 11 x 12 ⋯ x 1 d x 21 x 22 ⋯ x 2 d ⋮ ⋮ ⋮ ⋮ x n 1 x n 2 ⋯ x n d ] n × d = [ c 1 c 2 c 3 ⋅ ⋅ ⋅ c d ] \mathrm{X_{n\times d}}=\left[\begin{array}{c} \mathbf{x_{1}^{T}} \\ \mathbf{x_{2}^{T}} \\ \vdots \\ \mathbf{x_{n}^{T}} \end{array}\right]=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 d} \\ x_{21} & x_{22} & \cdots & x_{2 d} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n 1} & x_{n 2} & \cdots & x_{n d} \end{array}\right]_{n\times d}=[c_{1}\quad c_{2}\quad c_{3}\cdot\cdot\cdot c_{d}] Xn×d=⎣⎢⎢⎢⎡x1Tx2T⋮xnT⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋮⋯x1dx2d⋮xnd⎦⎥⎥⎥⎤n×d=[c1c2c3⋅⋅⋅cd]
step2:求出随机变量的均值 c ˉ i \bar c_{i} cˉi
求出随机变量的均值,即这里的每一列的均值,分别记作: [ c ˉ 1 c ˉ 2 c ˉ 3 ⋅ ⋅ ⋅ c ˉ d ] [\bar c_{1}\quad \bar c_{2}\quad \bar c_{3}\cdot\cdot\cdot \bar c_{d}] [cˉ1cˉ2cˉ3⋅⋅⋅cˉd]
step3: X n × d X_{n\times d} Xn×d 对应的列减去此列的均值,求得矩阵 C C C
X n × d X_{n\times d} Xn×d的对应的列减去此列的均值,得到矩阵 C C C:
C n × d = [ x 11 − c ˉ 1 x 12 − c ˉ 2 ⋯ x 1 d − c ˉ d x 21 − c ˉ 1 x 22 − c ˉ 2 ⋯ x 2 d − c ˉ d ⋮ ⋮ ⋮ ⋮ x n 1 − c ˉ 1 x n 2 − c ˉ 2 ⋯ x n d − c ˉ d ] n × d C_{n\times d}=\left[\begin{array}{cccc} x_{11}-\bar c_{1} & x_{12}-\bar c_{2} & \cdots & x_{1 d}-\bar c_{d} \\ x_{21}-\bar c_{1} & x_{22}-\bar c_{2} & \cdots & x_{2 d}-\bar c_{d} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n 1}-\bar c_{1} & x_{n 2}-\bar c_{2} & \cdots & x_{n d}-\bar c_{d} \end{array}\right]_{n\times d} Cn×d=⎣⎢⎢⎢⎡x11−cˉ1x21−cˉ1⋮xn1−cˉ1x12−cˉ2x22−cˉ2⋮xn2−cˉ2⋯⋯⋮⋯x1d−cˉdx2d−cˉd⋮xnd−cˉd⎦⎥⎥⎥⎤n×d
step4: 求协方差矩阵
协方差矩阵:
COV d × d = 1 n − 1 [ cov ( c 1 , c 1 ) cov ( c 1 , c 2 ) ⋯ cov ( c 1 , c d ) cov ( c 2 , c 1 ) cov ( c 2 , c 2 ) ⋯ cov ( c 2 , c d ) ⋮ ⋮ ⋮ ⋮ cov ( c d , c 1 ) cov ( c d , c 2 ) ⋯ cov ( c d , c d ) ] d × d = 1 n − 1 C d × n T C n × d \operatorname{COV}_{d\times d}=\frac{1}{n-1}\left[\begin{array}{cccc} \operatorname{cov}\left(c_{1}, c_{1}\right) & \operatorname{cov}\left(c_{1}, c_{2}\right) & \cdots & \operatorname{cov}\left(c_{1}, c_{d}\right) \\ \operatorname{cov}\left(c_{2}, c_{1}\right) & \operatorname{cov}\left(c_{2}, c_{2}\right) & \cdots & \operatorname{cov}\left(c_{2}, c_{d}\right) \\ \vdots & \vdots & \vdots & \vdots \\ \operatorname{cov}\left(c_{d}, c_{1}\right) & \operatorname{cov}\left(c_{d}, c_{2}\right) & \cdots & \operatorname{cov}\left(c_{d}, c_{d}\right) \end{array}\right]_{d\times d}=\frac{1}{n-1}C^{T}_{d\times n}C_{n\times d} COVd×d=n−11⎣⎢⎢⎢⎡cov(c1,c1)cov(c2,c1)⋮cov(cd,c1)cov(c1,c2)cov(c2,c2)⋮cov(cd,c2)⋯⋯⋮⋯cov(c1,cd)cov(c2,cd)⋮cov(cd,cd)⎦⎥⎥⎥⎤d×d=n−11Cd×nTCn×d
协方差矩阵的维度等于随机变量的个数,即列的维度。在某些场合下也会出现 1 n \frac{1}{n} n1,而不是 1 n − 1 \frac{1}{n-1} n−11
同理,协方差矩阵的定义2: X d × n X_{d\times n} Xd×n列表示样本,行表示随机变量(即特征)的时候
step1:找出随机变量 c i c_{i} ci
X d × n = [ x 1 , x 2 ⋯ x n ] = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋮ ⋮ x d 1 x d 2 ⋯ x d n ] d × n = [ c 1 c 2 ⋮ c d ] \mathrm{X_{d\times n}}=\left[\mathbf{x_{1}},\mathbf{x_{2}} \cdots\mathbf{x_{n}}\right]=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 n} \\ x_{21} & x_{22} & \cdots & x_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ x_{d 1} & x_{d 2} & \cdots & x_{d n} \end{array}\right]_{d\times n}=\left[\begin{array}{cccc} c_{1}\\ c_{2}\\ \vdots\\ c_{d}\end{array}\right] Xd×n=[x1,x2⋯xn]=⎣⎢⎢⎢⎡x11x21⋮xd1x12x22⋮xd2⋯⋯⋮⋯x1nx2n⋮xdn⎦⎥⎥⎥⎤d×n=⎣⎢⎢⎢⎡c1c2⋮cd⎦⎥⎥⎥⎤
step2:求出随机变量的均值 c ˉ i \bar c_{i} cˉi
求出随机变量的均值,即这里的每一行的均值,分别记作: [ c ˉ 1 c ˉ 2 ⋮ c ˉ d ] \left[\begin{array}{cccc} \bar c_{1}\\ \bar c_{2}\\ \vdots\\ \bar c_{d}\end{array}\right] ⎣⎢⎢⎢⎡cˉ1cˉ2⋮cˉd⎦⎥⎥⎥⎤
step3: X d × n X_{d\times n} Xd×n 对应的行减去此行的均值,求得矩阵 C C C
X d × n X_{d\times n} Xd×n的对应的行减去此行的均值,得到矩阵 C C C:
C d × n = [ x 11 − c ˉ 1 x 12 − c ˉ 1 ⋯ x 1 d − c ˉ 1 x 21 − c ˉ 2 x 22 − c ˉ 2 ⋯ x 2 d − c ˉ 2 ⋮ ⋮ ⋮ ⋮ x n 1 − c ˉ d x n 2 − c ˉ d ⋯ x n d − c ˉ d ] d × n C_{d\times n}=\left[\begin{array}{cccc} x_{11}-\bar c_{1} & x_{12}-\bar c_{1} & \cdots & x_{1 d}-\bar c_{1} \\ x_{21}-\bar c_{2} & x_{22}-\bar c_{2} & \cdots & x_{2 d}-\bar c_{2} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n 1}-\bar c_{d} & x_{n 2}-\bar c_{d} & \cdots & x_{n d}-\bar c_{d} \end{array}\right]_{d\times n} Cd×n=⎣⎢⎢⎢⎡x11−cˉ1x21−cˉ2⋮xn1−cˉdx12−cˉ1x22−cˉ2⋮xn2−cˉd⋯⋯⋮⋯x1d−cˉ1x2d−cˉ2⋮xnd−cˉd⎦⎥⎥⎥⎤d×n
step4: 求协方差矩阵
协方差矩阵:
COV d × d = 1 n − 1 [ cov ( c 1 , c 1 ) cov ( c 1 , c 2 ) ⋯ cov ( c 1 , c d ) cov ( c 2 , c 1 ) cov ( c 2 , c 2 ) ⋯ cov ( c 2 , c d ) ⋮ ⋮ ⋮ ⋮ cov ( c d , c 1 ) cov ( c d , c 2 ) ⋯ cov ( c d , c d ) ] d × d = 1 n − 1 C d × n C n × d T \operatorname{COV}_{d\times d}=\frac{1}{n-1}\left[\begin{array}{cccc} \operatorname{cov}\left(c_{1}, c_{1}\right) & \operatorname{cov}\left(c_{1}, c_{2}\right) & \cdots & \operatorname{cov}\left(c_{1}, c_{d}\right) \\ \operatorname{cov}\left(c_{2}, c_{1}\right) & \operatorname{cov}\left(c_{2}, c_{2}\right) & \cdots & \operatorname{cov}\left(c_{2}, c_{d}\right) \\ \vdots & \vdots & \vdots & \vdots \\ \operatorname{cov}\left(c_{d}, c_{1}\right) & \operatorname{cov}\left(c_{d}, c_{2}\right) & \cdots & \operatorname{cov}\left(c_{d}, c_{d}\right) \end{array}\right]_{d\times d}=\frac{1}{n-1}C_{d\times n}C^{T}_{n\times d} COVd×d=n−11⎣⎢⎢⎢⎡cov(c1,c1)cov(c2,c1)⋮cov(cd,c1)cov(c1,c2)cov(c2,c2)⋮cov(cd,c2)⋯⋯⋮⋯cov(c1,cd)cov(c2,cd)⋮cov(cd,cd)⎦⎥⎥⎥⎤d×d=n−11Cd×nCn×dT
协方差矩阵的维度等于随机变量的个数,即列的维度。在某些场合下也会出现 1 n \frac{1}{n} n1,而不是 1 n − 1 \frac{1}{n-1} n−11
协方差矩阵的定义1和定义2详细过程
当 X n × d X_{n\times d} Xn×d矩阵的行表示样本,列表示特征的时候:
由协方差矩阵定义1的求解步骤可得:
x \mathbf{x} x是d 维向量
x = [ x 1 x 2 ⋮ x d ] \mathbf{x}=\left[\begin{array}{c} \mathrm{x}_{1} \\ \mathrm{x}_{2} \\ \vdots \\ \mathrm{x}_{\mathrm{d}} \end{array}\right] x=⎣⎢⎢⎢⎡x1x2⋮xd⎦⎥⎥⎥⎤
X X X是由n个d维多元向量组成的矩阵;即X含有n个样本,每个样本都是d维的向量, X是nxd的矩阵。
x 1 = [ x 11 x 12 ⋮ x 1 d ] \mathbf{x_{1}}=\left[\begin{array}{c} \mathrm{x}_{11} \\ \mathrm{x}_{12} \\ \vdots \\ \mathrm{x}_{\mathrm{1d}} \end{array}\right] x1=⎣⎢⎢⎢⎡x11x12⋮x1d⎦⎥⎥⎥⎤, x 2 = [ x 21 x 22 ⋮ x 2 d ] \mathbf{x_{2}}=\left[\begin{array}{c} \mathrm{x}_{21} \\ \mathrm{x}_{22} \\ \vdots \\ \mathrm{x}_{\mathrm{2d}} \end{array}\right] x2=⎣⎢⎢⎢⎡x21x22⋮x2d⎦⎥⎥⎥⎤, x 3 = [ x 31 x 32 ⋮ x 3 d ] \mathbf{x_{3}}=\left[\begin{array}{c} \mathrm{x}_{31} \\ \mathrm{x}_{32} \\ \vdots \\ \mathrm{x}_{\mathrm{3d}} \end{array}\right] x3=⎣⎢⎢⎢⎡x31x32⋮x3d⎦⎥⎥⎥⎤
则
X n × d = [ x 1 T x 2 T ⋮ x n T ] = [ x 11 x 12 ⋯ x 1 d x 21 x 22 ⋯ x 2 d ⋮ ⋮ ⋮ ⋮ x n 1 x n 2 ⋯ x n d ] n × d = [ c 1 c 2 c 3 ⋅ ⋅ ⋅ c d ] \mathrm{X_{n\times d}}=\left[\begin{array}{c} \mathbf{x_{1}^{T}} \\ \mathbf{x_{2}^{T}} \\ \vdots \\ \mathbf{x_{n}^{T}} \end{array}\right]=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 d} \\ x_{21} & x_{22} & \cdots & x_{2 d} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n 1} & x_{n 2} & \cdots & x_{n d} \end{array}\right]_{n\times d}=[c_{1}\quad c_{2}\quad c_{3}\cdot\cdot\cdot c_{d}] Xn×d=⎣⎢⎢⎢⎡x1Tx2T⋮xnT⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋮⋯x1dx2d⋮xnd⎦⎥⎥⎥⎤n×d=[c1c2c3⋅⋅⋅cd]
step1:
按列算均值,得到第 j j j 列的均值 μ j \mu_{j} μj 如下:
μ j = Σ i = 1 n x i j n \mu_{j} = \frac{\overset{n}{\underset{i=1}{\Sigma}}x_{ij}}{n} μj=ni=1Σnxij
则 X X X的均值记为 μ \mu μ, μ \mathbf{\mu} μ是d 维向量
μ = [ μ 1 , μ 2 , μ 3 , ⋅ ⋅ ⋅ , μ d ] = [ c ˉ 1 c ˉ 2 c ˉ 3 ⋅ ⋅ ⋅ c ˉ d ] \mathbf{\mu}=\left[\mu_{1}, \mu_{2},\mu_{3},\cdot\cdot\cdot ,\mu_{d}\right]=[\bar c_{1}\quad \bar c_{2}\quad \bar c_{3}\cdot\cdot\cdot \bar c_{d}] μ=[μ1,μ2,μ3,⋅⋅⋅,μd]=[cˉ1cˉ2cˉ3⋅⋅⋅cˉd]
step2:
将 X X X的每一列减去平均值
C n × d = [ x 11 − c ˉ 1 x 12 − c ˉ 2 ⋯ x 1 d − c ˉ d x 21 − c ˉ 1 x 22 − c ˉ 2 ⋯ x 2 d − c ˉ d ⋮ ⋮ ⋮ ⋮ x n 1 − c ˉ 1 x n 2 − c ˉ 2 ⋯ x n d − c ˉ d ] n × d \mathbf{C_{n\times d}}=\left[\begin{array}{cccc} x_{11}-\bar c_{1} & x_{12}-\bar c_{2} & \cdots & x_{1 d}-\bar c_{d} \\ x_{21}-\bar c_{1} & x_{22}-\bar c_{2} & \cdots & x_{2 d}-\bar c_{d} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n 1}-\bar c_{1} & x_{n 2}-\bar c_{2} & \cdots & x_{n d}-\bar c_{d} \end{array}\right]_{n\times d} Cn×d=⎣⎢⎢⎢⎡x11−cˉ1x21−cˉ1⋮xn1−cˉ1x12−cˉ2x22−cˉ2⋮xn2−cˉ2⋯⋯⋮⋯x1d−cˉdx2d−cˉd⋮xnd−cˉd⎦⎥⎥⎥⎤n×d
step3:
计算协方差矩阵:
Σ d × d = C O V = 1 n − 1 . C T d × n . C n × d \Sigma_{d\times d}=COV=\frac{1}{n-1}.\mathbf{C^{T}}_{d\times n}.\mathbf{C}_{n\times d} Σd×d=COV=n−11.CTd×n.Cn×d
方法②:
当 X d × n X_{d\times n} Xd×n 矩阵,行表示特征,列表示样本的时候
由协方差矩阵的定义2得:
X X X是由n个d维多元向量组成的矩阵;即X含有n个样本,每个样本都是d维的向量,X是dxn的矩阵
x 1 = [ x 11 x 12 ⋮ x 1 d ] \mathbf{x_{1}}=\left[\begin{array}{c} \mathrm{x}_{11} \\ \mathrm{x}_{12} \\ \vdots \\ \mathrm{x}_{\mathrm{1d}} \end{array}\right] x1=⎣⎢⎢⎢⎡x11x12⋮x1d⎦⎥⎥⎥⎤, x 2 = [ x 21 x 22 ⋮ x 2 d ] \mathbf{x_{2}}=\left[\begin{array}{c} \mathrm{x}_{21} \\ \mathrm{x}_{22} \\ \vdots \\ \mathrm{x}_{\mathrm{2d}} \end{array}\right] x2=⎣⎢⎢⎢⎡x21x22⋮x2d⎦⎥⎥⎥⎤, x 3 = [ x 31 x 32 ⋮ x 3 d ] \mathbf{x_{3}}=\left[\begin{array}{c} \mathrm{x}_{31} \\ \mathrm{x}_{32} \\ \vdots \\ \mathrm{x}_{\mathrm{3d}} \end{array}\right] x3=⎣⎢⎢⎢⎡x31x32⋮x3d⎦⎥⎥⎥⎤
则
X d × n = [ x 1 , x 2 , ⋅ ⋅ ⋅ , x n ] = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋮ ⋮ x d 1 x d 2 ⋯ x d n ] d × n = [ c 1 c 2 ⋮ c d ] \mathrm{X_{d\times n}}=\left[\mathbf{x_{1}},\mathbf{x_{2}},\cdot\cdot\cdot,\mathbf{x_{n}}\right]=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 n} \\ x_{21} & x_{22} & \cdots & x_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ x_{d 1} & x_{d 2} & \cdots & x_{d n} \end{array}\right]_{d\times n}=\left[\begin{array}{c} \mathrm{c}_{1} \\ \mathrm{c}_{2} \\ \vdots \\ \mathrm{c}_{\mathrm{d}} \end{array}\right] Xd×n=[x1,x2,⋅⋅⋅,xn]=⎣⎢⎢⎢⎡x11x21⋮xd1x12x22⋮xd2⋯⋯⋮⋯x1nx2n⋮xdn⎦⎥⎥⎥⎤d×n=⎣⎢⎢⎢⎡c1c2⋮cd⎦⎥⎥⎥⎤
step1:
按行算均值,得到第 i i i 行的均值 μ i \mu_{i} μi 如下:
μ i = Σ j = 1 n x i j n \mu_{i} = \frac{\overset{n}{\underset{j=1}{\Sigma}}x_{ij}}{n} μi=nj=1Σnxij
则 X X X的均值记为 μ \mu μ, μ \mathbf{\mu} μ是d 维向量
则按行算均值: μ = [ μ 1 μ 2 ⋮ μ d ] = [ c ˉ 1 c ˉ 2 ⋮ c ˉ d ] \mu=\left[\begin{array}{c} \mathrm{\mu}_{1} \\ \mathrm{\mu}_{2} \\ \vdots \\ \mathrm{\mu}_{\mathrm{d}} \end{array}\right]=\left[\begin{array}{c} \mathrm{\bar c}_{1} \\ \mathrm{\bar c}_{2} \\ \vdots \\ \mathrm{\bar c}_{\mathrm{d}} \end{array}\right] μ=⎣⎢⎢⎢⎡μ1μ2⋮μd⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡cˉ1cˉ2⋮cˉd⎦⎥⎥⎥⎤
step2:
将 X X X的每一行减去平均值
C d × n = [ x 11 − c ˉ 1 x 12 − c ˉ 1 ⋯ x 1 n − c ˉ 1 x 21 − c ˉ 2 x 22 − c ˉ 2 ⋯ x 2 n − c ˉ 2 ⋮ ⋮ ⋮ ⋮ x d 1 − c ˉ d x d 2 − c ˉ d ⋯ x d n − c ˉ d ] d × n \mathbf{C}_{d\times n}=\left[\begin{array}{cccc} x_{11}-\bar c_{1} & x_{12}-\bar c_{1} & \cdots & x_{1 n}-\bar c_{1} \\ x_{21}-\bar c_{2} & x_{22}-\bar c_{2} & \cdots & x_{2 n}-\bar c_{2} \\ \vdots & \vdots & \vdots & \vdots \\ x_{d 1}-\bar c_{d} & x_{d 2}-\bar c_{d} & \cdots & x_{d n}-\bar c_{d} \end{array}\right]_{d\times n} Cd×n=⎣⎢⎢⎢⎡x11−cˉ1x21−cˉ2⋮xd1−cˉdx12−cˉ1x22−cˉ2⋮xd2−cˉd⋯⋯⋮⋯x1n−cˉ1x2n−cˉ2⋮xdn−cˉd⎦⎥⎥⎥⎤d×n
step3:
计算协方差:
Σ d × d = C O V = 1 n − 1 . C d × n . C T n × d \Sigma_{d\times d}=COV=\frac{1}{n-1}.\mathbf{C}_{d\times n}.\mathbf{C^{T}}_{n\times d} Σd×d=COV=n−11.Cd×n.CTn×d
但是numpy里面的cov好像是按 定义2 中方法来计算的,即 X d × n X_{d\times n} Xd×n
老师上课讲的时候是按第一种方法来计算的
Example
np.cov(m, y=None,rowvar=True, bias=False, ddof=None, fweights=None, aweights=None, *, dtype=None)
参数解释:
m为要计算的 向量or 矩阵
rowvar默认为True,即默认每一行为一个变量,每一列为一个观测值,即每一列为一个样本,每一行为一个特征变量
import numpy as np
x = [[1,2,3],[3,1,1]]
a=np.cov(x)
print(a)
# 在np中,默认输入的矩阵为Xdxn,即按方法2求协方差矩阵
# 所以,计算Xnxd则需要转置为Xdxn,即X需要转为行表示特征,列表示样本,
# 计算出来的才是正确的协方差矩阵
xT = [[1,3],[2,1],[3,1]]
print(xT)
b = np.cov(xT)
print(b)
# np.cov(m, rowvar=False)来直接计算Xnxd的协方差矩阵
print("-"*20)
print(np.cov(x, rowvar=False))

np.cov求协方差矩阵参考博客
np.cov参考博客
np.cov官网
对矩阵X,含有2个样本,每个样本有3个特征
因为X矩阵的行表示样本,列表示特征,所以要用方法①计算:
X 2 × 3 = [ x 1 T x 2 T ] = [ x 11 x 12 x 13 x 21 x 22 x 23 ] 2 × 3 = [ 1 2 3 3 1 1 ] 2 × 3 \mathrm{X_{2\times 3}}=\left[\begin{array}{c} \mathbf{x_{1}^{T}} \\ \mathbf{x_{2}^{T}} \\ \end{array}\right]=\left[\begin{array}{cccc} x_{11} & x_{12} & x_{1 3} \\ x_{21} & x_{22} & x_{2 3} \end{array}\right]_{2\times 3}=\left[\begin{array}{cccc} 1 & 2& 3 \\ 3& 1 & 1 \end{array}\right]_{2\times 3} X2×3=[x1Tx2T]=[x11x21x12x22x13x23]2×3=[132131]2×3
按方法①手动计算,就得到协方差矩阵 Σ = [ 2 − 1 − 2 − 1 0.5 1 − 2 1 2 ] 3 × 3 \Sigma=\left[\begin{array}{cccc} 2 & -1& -2 \\ -1& 0.5 & 1 \\ -2& 1 & 2 \end{array}\right]_{3\times 3} Σ=⎣⎡2−1−2−10.51−212⎦⎤3×3
协方差矩阵的意义
在概率论中,两个随机变量X,Y之间相互关系,大致有下列3种情况:
case1:
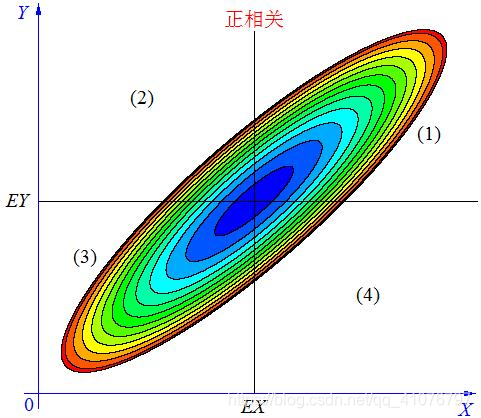
情况一,如上, 当 X, Y 的联合分布像上图那样时,我们可以看出,大致上有: X 越大 Y 也越大, X 越小 Y 也越小,这种情况,我们称为“正相关”。
case2:
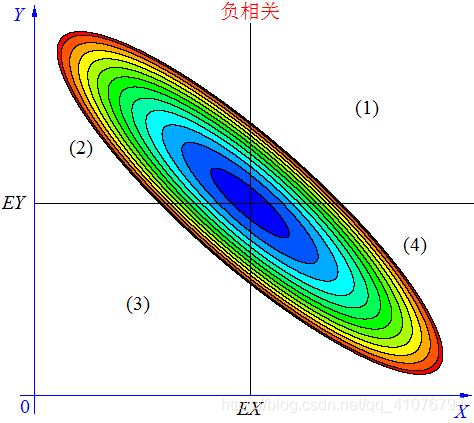
情况二, 如上图, 当X, Y 的联合分布像上图那样时,我们可以看出,大致上有:X 越大Y 反而越小,X 越小 Y 反而越大,这种情况,我们称为“负相关”。
case3:
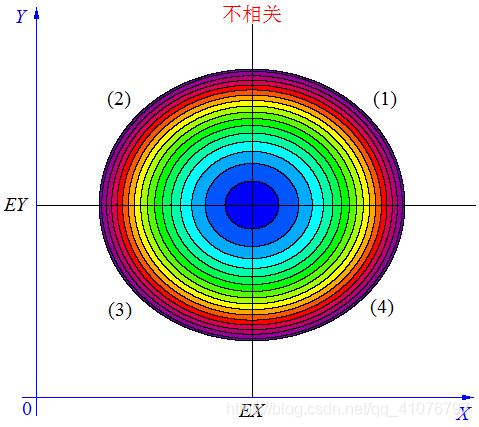
情况三,如上图, 当X, Y 的联合分布像上图那样时,我们可以看出:既不是X 越大Y 也越大,也不是 X 越大 Y 反而越小,这种情况我们称为“不相关”。
怎样将这3种相关情况,用一个简单的数字表达出来呢?
-
在图中的区域(1)中,有 X>EX ,Y-EY>0 ,所以(X-EX)(Y-EY)>0;
在图中的区域(2)中,有 X<EX ,Y-EY>0 ,所以(X-EX)(Y-EY)<0;
在图中的区域(3)中,有 X<EX ,Y-EY<0 ,所以(X-EX)(Y-EY)>0;
在图中的区域(4)中,有 X>EX ,Y-EY<0 ,所以(X-EX)(Y-EY)<0。 -
当X 与Y 正相关时,它们的分布大部分在区域(1)和(3)中,小部分在区域(2)和(4)中,所以平均来说,有E(X-EX)(Y-EY)>0 。
当 X与 Y负相关时,它们的分布大部分在区域(2)和(4)中,小部分在区域(1)和(3)中,所以平均来说,有(X-EX)(Y-EY)<0 。
当 X与 Y不相关时,它们在区域(1)和(3)中的分布,与在区域(2)和(4)中的分布几乎一样多,所以平均来说,有(X-EX)(Y-EY)=0 。 -
所以,我们可以定义一个表示X, Y 相互关系的数字特征,也就是协方差
cov(X, Y) = E[(X-EX)(Y-EY)]
当 cov(X, Y)>0时,表明 X与Y 正相关;
当 cov(X, Y)<0时,表明X与Y负相关;
当 cov(X, Y)=0时,表明X与Y不相关。
且绝对值越大,相关性越大。
这就是协方差的意义。 -
上面是协方差的意义,协方差堆在一起就组成了协方差矩阵。