嵌入式软件算法之卡尔曼滤波基本原理浅析

---

---

前言

   卡尔曼滤波是一种实时性高，滤波效果好并且计算量小的一种滤波算法，因内存占用不大的适合嵌入式使用而广受欢迎。相较于常见的经典滤波方式卡尔曼滤波使用上简单方便，但涉及到概率分布模型以及迭代存在一定的入门门槛。
   本文从卡尔曼滤波基本原理入手，通过讲解卡尔曼基本迭代过程及一阶多阶例程来实现对卡尔曼基本原理的剖析。

一、卡尔曼滤波介绍

60年代初，卡尔曼(R．E．Kalman)和布塞(R． S．Bucy)发表了一篇重要的论文《线性滤波和预测 理论的新成果》，提出了一种新的线性滤波和预测理论，被称之为卡尔曼滤波。特点是在线性状态空间表示的基础上对有噪声的输入和观测信号进行处理，求取系统状态或真实信号。
这种理论是在时间域上来表述的，基本的概念是：在线性系统的状态空间表示基础上，从输出和输入观测数据求系统状态的最优估计。这里所说的系统状态，是总结系统所有过去的输入和扰动对系统的作用的最小参数的集合，知道了系统的状态就能够与未来的输入与系统的扰动一起确定系统的整个行为。
自从卡尔曼滤波理论问世以来，在通信系统、电力系统、航空航天、环境污染控制、工业控制、雷达信号处理等许多部门都得到了应用，取得了许多成功应用的成果。例如在图像处理方面，应用卡尔曼滤波对由于某些噪声影响而造成模糊的图像进行复原[1]。

二、基本原理

卡尔曼滤波可以认为是贝叶斯滤波的一种特例，本质上都是根据贝叶斯公式叠加似然概率与先验概率得到后验概率。从最本质的原理去理解需要概率论很多的知识储备，但从使用形式上理解就比较简单。
从形式上理解是测量值与估计值的权重叠加，为了便于叠加对测量值以及估计值采用高斯分布模型来描述期望值及误差，然后利用高斯分布模型的公式性质对估计值与测量值进行叠加输出，计算出最优值误差范围。下一周期的滤波过程与当前过程一致，不断进行迭代即可。

2.1 测量值与估计值的权重配置

KMF的基本理解应从最终输出的最优值公式入手：

上式中x-表示最优输出值，x^为估计值，z为测量值，kg表示卡尔曼增益。

从式子中即可看出卡尔曼滤波与一阶低通滤波、互补滤波形式一致，依靠权重系数kg来影响最终输出值。预测值的来源依靠控制系统模型，如：当前温度为30°，以10°每秒的功率加热可预测出2秒后温度为50°(忽略散热等影响)，误差为5度。当然在简单的一阶滤波情况下控制模型可以简化，一直默认1s后的预测值为之前的实际最优输出值即可。测量值从传感器处获得，误差的大小从传感器手册上获取。
这样我们理解到了：

当前输出最优值 = 估计值 + 卡尔曼增益(权重) * ( 测量值 - 估计值 )
与一阶低通滤波不同，卡尔曼滤波的优势在于权重并不是一个固定值，会随着不断地迭代计算而进行变化。因此要想理清卡尔曼滤波算法，就要了解卡尔曼增益系数是如何来的。卡尔曼增益系数的获得得益于高斯分布数学模型。

2.2 高斯分布数学模型的描述

从上边我们知道了最优输出值是估计值与测量值的叠加，但估计值与测量值并不是一个准确的值存在一定的误差，如传感器测量温度，测量值为30度，误差为2°；估计值也会应为模型的准确程度存在计算过程的过程误差，以及外部的干扰误差。高斯分布期望与方差形式和这种值与误差的形式一致，非常适合描述这个模型。
因此卡尔曼将高斯概率分布模型来具体函数化描述各个分量值及其误差，将误差值的量间接引入。
高斯分布又叫正态分布，其概率密度函数如下所示：

e为自然底数；σ ^2为方差，对应误差；μ为期望，对应估计值/测量值

函数图形如下

通过对某一段区间的积分可得数值在这个区间的概率。整个积分区间面积为1。σ ^2方差值越大函数图形越“胖矮”反之“高瘦”，μ期望决定了函数图形在X轴上的偏移。
假设测量值为30，方差为3，估计值为32，方差为4，则如图所示：

其中红色线条表示测量值，蓝色线条表示估计值。

上图可看出两种图像具有重叠部分，重叠部分的置信区间表示此部分的数值既满足估计值的概率分布又满足测量值的概率分布，因此我们希望估计值与测量值叠加后的值分布在此区域内。为实现此效果可采用高斯分布的叠加性质。
高斯分布概率密度公式是指数形式，两个高斯分布的概率密度函数的乘机仍旧满足高斯分布。下面推导一下叠加过程：

1.假设估计值与测量值的高斯分布概率密度函数分别为：

2.根据高斯公式的性质进行相乘：
此部分为卡尔曼滤波的核心部分，叠加原理公式是贝叶斯公式：后验概率=k x似然概率 x 先验估计概率。对应下就是最优输出概率密度函数=k x 测量值概率密度函数 x 估计值概率密度函数。

3.化简并构造新的高斯公式形态

Sg称为压缩系数，决定了总概率面积的大小
3.修正Sg系数
由上可看出乘积后叠加出的公式并不完全满足高斯分布的所有性质，因为Sg的为常数项会使总面积(总概率)放大或者缩小，所以为便于高斯分布的迭代，令Sg=1，并不改变实际的最优输出期望值u，及误差，则叠加后的数值仍满足高斯分布的所有性质。

继续对之前的测量值为30，方差为3，估计值为32，方差为4，进行叠加不改变Sg的大小：

其中红色线条表示测量值，蓝色线条表示估计值，绿色线条表示概率密度函数叠加。

令Sg系数为1，可得新的分布函数图形：

其中红色线条表示测量值，蓝色线条表示估计值，绿色线条表示修正后的概率密度函数。

6.变换叠加后的方差σ ^2与期望μ，提取卡尔曼增益系数Kg



至此已完成对估计值、测量值的高斯分布描述以及叠加，根据叠加后的期望值u便得出最优估计值，叠加后的方差用于下一次估计值方差计算。
单次叠加完成后，后续便是相同的迭代过程

2.3 基于高斯分布模型的迭代

卡尔曼滤波的本质就是高斯分布模型的迭代过程，这里进行一次迭代梳理：
总共可分为三部分：

1. 估计值高斯分布模型的建立–预测
   高斯分布模型的建立需要两个参数：期望μ(估计值)和方差σ^2。
   估计值与控制模型有关，如：当前温度为30°，以10°每秒的功率加热可预测出2秒后温度为50°(忽略散热等影响)，一般一阶卡尔曼将估计值与上一次最优输出值保持一致即30°。
   估计值方差σ² 与控制模型和外界干扰噪声有关，在上一次最优输出误差基础上控制模型会将误差进行传递，因此存在过程噪声，若外部存在干扰则误差加大，因此新的方差 σ² =上一次最优输出方差*a+q;一般一阶卡尔曼滤波会简化使得a=1,只考虑干扰存在的噪声q即可，去也是卡尔曼滤波需要调参的参数之一。
   
2. 测量值高斯分布模型的建立–观测
   测量值高斯分布模型的期望值μ由传感器实时的测量值得到，方差σ²由传感器手册获取，如果找不到可以测量一组数据根据方差公式计算一个，方差一般确定了不会改变。
   
3. 叠加高斯分布模型的建立–更新
   叠加过程就是先求出卡尔曼增益，然后求出叠加后高斯分布的期望值(最优输出值)，同时求出叠加后高斯分布的方差。
   
   
   
   用数学公式描述整个过程就是6个公式：
   估计值及方差计算(预测)：
   
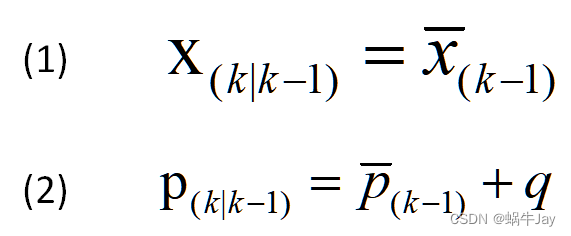
   测量值及方差获取(观测)：
   
   最优输出值及方差计算(更新)：
   先计算卡尔曼增益
   
   
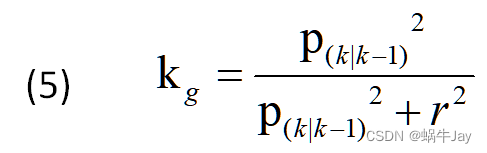
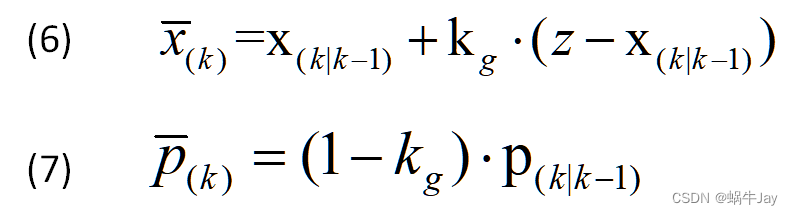
   公式3、4需要从传感器处获取，其余的公式1、2、4、5、6、7为最常见的卡尔曼滤波迭代计算公式。

三、一阶卡尔曼滤波

一阶卡尔曼滤波最容易理解也是最容易入手的突破口，基本原理讲完套一下示例更容易理解整个过程。

3.1温度示例模型

我们要研究一个房间的温度，估算k时刻的实际温度值。

1. 估计值高斯分布(预测)
   首先你要根据k-1时刻的温度值，来预测k时刻的温度(K时刻的经验温度) 。因为你相信温度是恒定的，所以你会得到k时刻的温度预测值是跟k-1时刻一样的，假设是23度(公式（1）)，同时该预测值的高斯噪声的方差是5(5是这样得到的:如果k-1时刻估算出的最优温度值的方差是3，存在一些散热的干扰因素2，相加就是5 (公式(2)) )。
2. 测量值高斯分布(观测)
   然后，你从温度计那里得到了k时刻的温度值，假设是25度，同时该值的样本方差是4度。
3. 最优输出值高斯分布(更新)
   现在，我们用于估算K时刻房间的实际温度有两个温度值:估计值23度和测量值25度。究竞实际温度是多少呢?是相信自己还是相信温度计?究竟相信谁多一点?我们需要用他们的方差来判断。H=55/(55+44)=0.61 (公式(5))，所以我们可以估算出K时刻的最优温度值为: 23+ 0.61(25-23)=24.22度(公式(6))得到了K时刻的最优温度，因为K+1时刻的估计温度值的方差计算需要得到K时刻的最优温度(24.22) 的方差，所以也需要更新最优温度的方差，(1-H)*5 =1.95(公式(7))。
   就这样，卡尔曼滤波器就不断的把误差递归，从而估算出最优的温度值，运行速度快，且只保留上一时刻的协方差。

3.2 一阶卡尔曼滤波简化说明

一阶卡尔曼滤波可以做很多简化，体现在以下几点：

1. 简化控制模型，当前估计值与上一次最优输出值相同，略过了控制作用。
2. 简化控制对估计值误差的传递，一般估计值的方差直接在上一次最优输出值方差的基础上叠加外部干扰噪声，其实外部干扰噪声也可以省略(具体效果没有对比过)。

3.3 一阶卡尔曼滤波代码

提供了两个一阶版本，一种通用型的，一种省略了噪声q，并且将迭代能融合的过程公式进行了融合，但未测试仅供借鉴。

3.3.1 基本通用型版本

.h文件

#ifndef __PUB_KMF
#define __PUB_KMF
typedef struct 
{
    
    
		float p;//最优输出方差
		float q;//噪声
		float r;//传感器方差
		float Kg;//卡尔曼增益
		float x;//最优输出
	
}ST_KMF;

class pub_kmf
{
    
    

	/*---------DATA-----------*/		
	public:
	ST_KMF st_kmf;	
	/*------------FUNCTION----------*/	
	public:
		  pub_kmf(){
    
    };
		  ~pub_kmf(){
    
    };	
	void  InitValue(void);
	float KalmanFilter(ST_KMF *st_kmf,float sensorVal);
		
};

#endif

.cpp文件

#include"pub_KMF.h"

pub_kmf st_kmf;

void pub_kmf::InitValue(void)
{
    
    
	st_kmf.q  =0.1;
	st_kmf.r  =0.2;
	st_kmf.p  =0;
	st_kmf.Kg =0;
	st_kmf.x  =0;
}

float pub_kmf::KalmanFilter(ST_KMF *st_kmf,float sensorVal)
{
    
    
	//计算估计值
	st_kmf->x = 1*st_kmf->x
	//计算估计值方差
	st_kmf->p = st_kmf->p +st_kmf->q;
	//计算卡尔曼增益
	st_kmf->Kg = (st_kmf->p*st_kmf->p)/(st_kmf->p*st_kmf->p+st_kmf->r*st_kmf->r);
	//计算最优输出
	st_kmf->x =	st_kmf->x +st_kmf->Kg*(sensorVal-st_kmf->x);
	//计算最优输出方差
	st_kmf->p = (1-st_kmf->Kg)*st_kmf->p;
}

3.3.2 最简化版本

.h文件

#ifndef __PUB_KMF
#define __PUB_KMF
typedef struct 
{
    
    
		float p;//最优输出方差
		//float q;//噪声
		float r;//传感器方差
		//float Kg;//卡尔曼增益
		float x;//最优输出
	
}ST_KMF;

void  InitValue(void);
float KalmanFilter(ST_KMF *st_kmf,float sensorVal);
extern 	ST_KMF st_kmf;	
#endif

.c文件

#include"pub_KMF.h"

ST_KMF st_kmf;	

void InitValue(void)
{
    
    
	st_kmf.r  =0.2;
	st_kmf.p  =0.1;
	//st_kmf.Kg =0;
	st_kmf.x  =0;
}

float KalmanFilter(ST_KMF *st_kmf,float sensorVal)
{
    
    
	//计算估计值
	//st_kmf->p = st_kmf->p
	//计算估计值方差
	//st_kmf->p = st_kmf->p;
	//计算卡尔曼增益
	//st_kmf->Kg = (st_kmf->p*st_kmf->p)/(st_kmf->p*st_kmf->p+st_kmf->r*st_kmf->r);
	//计算最优输出
	st_kmf->x =	st_kmf->x +((st_kmf->p*st_kmf->p)/(st_kmf->p*st_kmf->p+st_kmf->r*st_kmf->r))*(sensorVal-st_kmf->x);
	//计算最优输出方差
	st_kmf->p = ((st_kmf->r*st_kmf->r)/(st_kmf->p*st_kmf->p+st_kmf->r*st_kmf->r))*st_kmf->p;
}

---

四、多阶卡尔曼滤波

多阶卡尔曼滤波与一阶原理一致，不同点在于：

• 必须添加控制模型，哪怕再简单的控制模型也要体现出状态参数之间的关系，如机器人运动过程中的位置与速度。否则的话本质还是一阶，多阶模型非常适合多传感器数据的融合。
• 方差变为协方差，不仅体现误差还展现了转态参数之间的相关性信息。
• 由普通线性方程计算转换为矩阵运算。
• 容易融合多传感器数据
  本节在一阶原理的基础上进行讲解，侧重于体现多阶的运算过程，以二阶的机器人位置速度模型为操作示例，更多阶的模型基本原理与此一致。
  参考示例
  一个机器人在平地上进行移动，为了实现位置与速度的控制对机器人增加了位置与速度传感器，用来反馈位置与速度。
  
  于是可用x来表示机器人当前的状态，包含了机器人的位置及速度分量，称为状态向量，状态向量的表现形式如下：
  

建立小车的运动学模型

矩阵表示上式：

F为状态转移矩阵。B为控制矩阵。
当然完整一点也会有噪声出现wk。

此时输出的x则为先验估计，也就是估计值。
对应估计值的便是估计值方差了，但多状态量间并非相互独立的，因此存在不同量间的方差计算不再是单一量的离散程度，而变成了两个量间的相关性，统一用协方差表示。

机器人位置速度模型的协方差则为

先验估计的协方差更新如下式所示：

状态转移矩阵的加入表明误差会跟随状态转移进行转移，Q表示估计的噪声
此时已经完成估计值模型的更新，下面就是测量值模型，也叫做后验估计模型。

注意，传感器的输出值不一定就是我们创建的状态向量当中的元素，有时候需要进行一下简单的换算。即使是，有可能单位也不对应，所以，需要一个转换。这个转换就是矩阵，在一些文献当中也被称作状态空间到观测空间的映射矩阵。举个例子，传感器仅能测量位置与速度，但计算需要状态向量增加一个加速度，加速度值可由速度单位时间内变化量计算得到，因此测量向量为2x1矩阵，状态向量为3x1矩阵，中间需要一个3x3的转换矩阵。当然测量量中也可添加测量噪声Vk。对应的测量协方差[1]。

测量模型更新完毕，下边就需要进行模型叠加。根据一阶卡尔曼滤波叠加公式，先计算出卡尔曼增益系数，再计算出最优输出及方差推导出多阶卡尔曼增益系数矩阵、最优状态向量以及对应的协方差：一阶


二阶

过程、原理与一阶一致，协方差以及矩阵的运算会使得运算看起来变得复杂起来，实则对多传感器多状态参数的处理提供了极大的方便。

五、参数调整

参数调整参考这篇文章
先摘取部分便于使用：
Q值为过程噪声，越小系统越容易收敛，我们对模型预测的值信任度越高；但是太小则容易发散，如果Q为零，那么我们只相信预测值；Q值越大我们对于预测的信任度就越低，而对测量值的信任度就变高；如果Q值无穷大，那么我们只信任测量值；R值为测量噪声，太小太大都不一定合适。R太大，卡尔曼滤波响应会变慢，因为它对新测量的值的信任度降低；越小系统收敛越快，但过小则容易出现震荡；测试时可以保持陀螺仪不动，记录一段时间内陀螺仪的输出数据，这个数据近似正态分布，按3σ原则，取正态分布的(3σ)²作为R的初始化值。
测试时可以先将Q从小往大调整，将R从大往小调整；先固定一个值去调整另外一个值，看收敛速度与波形输出。
系统中还有一个关键值P，它是误差协方差初始值，表示我们对当前预测状态的信任度，它越小说明我们越相信当前预测状态；它的值决定了初始收敛速度，一般开始设一个较小的值以便于获取较快的收敛速度。随着卡尔曼滤波的迭代，P的值会不断的改变，当系统进入稳态之后P值会收敛成一个最小的估计方差矩阵，这个时候的卡尔曼增益也是最优的，所以这个值只是影响初始收敛速度。

六、卡尔曼滤波扩展

卡尔曼滤波虽然是实时性很强的滤波但仅针对线性系统（状态转移为线性关系，即当前估计值Xk与上一次最优Xk-1成比例），对误差的估计仅基于规定好的传感器误差以及计算噪声误差，并不一种针对实际过程过程进行统计计算的误差并且进记录上一次的输出值。因此出现了扩展卡尔曼滤波的算法，不同之处在于估计与测量变成非线性的函数迭代形式，为了方便处理非线性部分采用泰勒一阶展开的形式间接转化为线性。

总结

大概梳理了一下一阶卡尔曼滤波的迭代以及原理，对高阶以及扩展的讲解较少，有兴趣的可以参考一下参考资料中的链接。
总过程分为三部分：预测、观测、更新。明白了这三个过程，设计程序参数修改基本就可以使用了。

参考资料

1. How a Kalman filter works, in pictures
2. 卡尔曼滤波
3. STM32应用(六)一阶卡尔曼滤波代码和简单应用
4. 两个高斯分布乘积的理论推导
5. 卡尔曼滤波中关键参数的调整
6. 滤波算法: 贝叶斯滤波