本文章是从其他地方总结一些对自己有用的理论,全文可在底部参考文章中查阅。
侵删,不断学习不断更新~
我们知道,矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
实际上,上述的一段话既讲了矩阵变换特征值及特征向量的几何意义(图形变换)也讲了其物理含义。物理的含义就是运动的图景:特征向量在一个矩阵的作用下作伸缩运动,伸缩的幅度由特征值确定。特征值大于1,所有属于此特征值的特征向量身形暴长;特征值大于0小于1,特征向量身形猛缩;特征值小于0,特征向量缩过了界,反方向到0点那边去了。
关于特征值和特征向量,这里请注意两个亮点。这两个亮点一个是线性不变量的含义,二个是振动的谱含义。
——《线性代数的几何意义》
如果存在某个或某些向量在A作用之后,它只是伸长或者缩短,其位置仍停留在其原来张成的直线上,那么称之为A的特征向量,伸长或者缩短的倍数称为对应特征向量的特征值。公式表达为:
A v ‾ = λ v ‾ , ∣ A − λ I ∣ = 0 (1) A\overline v=λ\overline v ,\quad|A−λI|=0 \tag{1} Av=λv,∣A−λI∣=0(1)
N N N 个特征向量就是 N N N 个标准正交基,而特征值的模则代表矩阵在每个基上的投影长度。
在查找相关资料时,知乎马同学大佬讲解的非常详细,这里再总结一下!特征值和特征向量,称为一个特征空间,如果反复乘一个矩阵,该向量会越贴合最大值所对应的特征向量!引用马同学知乎中的一张图。
[ x x + 1 y x + 1 ] = A [ x x y x ] \begin{bmatrix} x_{x+1} \\ y_{x+1}\\ \end{bmatrix} =A \begin{bmatrix} x_{x} \\ y_{x}\\ \end{bmatrix} [xx+1yx+1]=A[xxyx]
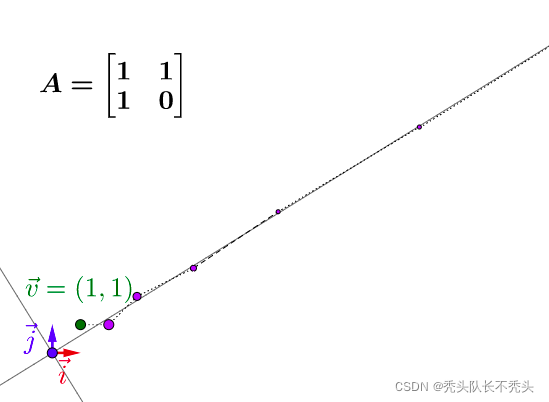
该向量会沿着特征值最大的特征空间的方向!一个很重要的性质!有大佬上传了视频到YouKu上面。
如果A为样本的协方差矩阵,特征值 λ \lambda λ 的大小就反映了变换后在特征向量方向上变换的幅度,幅度越大,说明这个方向上的元素差异也越大,换句话说这个方向上的元素更分散。
关于矩阵分解,就是为了得到特征值和特征向量,对于矩阵 A A A可以对角化的话,可以通过相似矩阵进行下面这样的特征值分解:
A = P ∧ P − 1 A = P\wedge P^{-1} A=P∧P−1
其中 ∧ \wedge ∧为对角阵, P P P的列向量是单位化的特征向量。特征值就是拉伸的比例,特征向量确定了拉伸的方向。
特征向量正交,这样变换后才能保证变换最大的方向在基方向。如果特征向量不正交就有可能不是变化最大的方向。
矩阵特征值是对特征向量进行伸缩和旋转程度的度量,实数是只进行伸缩,虚数是只进行旋转,复数就是有伸缩有旋转。其实最重要的是特征向量,从它的定义可以看出来,特征向量是在矩阵变换下只进行“规则”变换的向量,这个“规则”就是特征值。
1) A A A 和 A T A^{T} AT 有相同的特征值,但是特征向量不一定相同
证明: ∣ λ E − A T ∣ = ∣ λ E T − A T ∣ = ∣ ( λ E − A ) T ∣ = ∣ λ E − A ∣ = 0 |\lambda E-A^{T}| = |\lambda E^{T}-A^{T}|=|(\lambda E - A)^{T}|=|\lambda E-A|=0 ∣λE−AT∣=∣λET−AT∣=∣(λE−A)T∣=∣λE−A∣=0
2)若 ∑ ∣ a i j < 1 , j = 1 , 2 , . . . , n ∣ \sum|a_{ij}<1,j=1,2,...,n| \quad ∑∣aij<1,j=1,2,...,n∣ 且 ∑ ∣ a i j ∣ < 1 , j = 1 , 2 , . . . , n , ∑∣a_{ij}∣<1,j=1,2,...,n, ∑∣aij∣<1,j=1,2,...,n, 则 ∣ λ k ∣ < 1 |\lambda_{k}| < 1 ∣λk∣<1
3)若方阵的n个特征值为 λ 1 , λ 2 , . . . , λ n \lambda_{1},\lambda_{2},...,\lambda_{n} λ1,λ2,...,λn,则有① ∑ i = 1 n λ i = ∑ i = 1 n a i i \sum_{i=1}^{n}\lambda_{i} =\sum_{i=1}^{n}a_{ii} ∑i=1nλi=∑i=1naii,也就是所有的特征值之和就为矩阵对角线元素之和;② λ 1 , λ 2 , . . . , λ n = ∣ A ∣ \lambda_{1},\lambda_{2},...,\lambda_{n}=|A| λ1,λ2,...,λn=∣A∣
4)互不相同的特征值 λ 1 , λ 2 , . . . , λ n \lambda_{1},\lambda_{2},...,\lambda_{n} λ1,λ2,...,λn对应的特征向量 α 1 , α 2 , . . . , α n \alpha_{1},\alpha_{2},...,\alpha_{n} α1,α2,...,αn线性无关
5)对4)进行补充,如果每个特征向量有多对特征值,那么这些特征向量也是线性无关的
6) k k k 重特征根,对应的线性无关的特征向量的个数小于等于 k k k
其它性质:
1) k λ k\lambda kλ是 k A kA kA 的特征值
2) λ 2 \lambda^{2} λ2 是 A 2 A^{2} A2的特征值, λ k \lambda^{k} λk 是 A k A^{k} Ak 的特征值
3) 1 λ \frac{1}{\lambda} λ1 是 A − 1 A^{-1} A−1 的特征值; 1 λ ∣ A ∣ \frac{1}{\lambda}|A| λ1∣A∣ 是 A ∗ A^∗ A∗ 的特征值
参考文章:
1.特征值和特征向量
2.特征值(eigenvalue)特征向量(eigenvector)特征值分解(eigenvalue decomposition)
3.如何理解矩阵特征值?
4.【线性代数(13)】矩阵的特征值与特征向量含义及性质