ADPRL - 近似动态规划和强化学习 - Note 7 - Approximate Dynamic Programming

7. 近似动态规划 （Approximate Dynamic Programming）

在前面的章节中，我们研究了经典DP算法的理论基础和它们的高级变化。尽管这些算法具有良好的理论特性，但在许多实际应用中，这些算法仍然是低效的，甚至是不切实际的。这种现象主要是由于维数的诅咒，它在存储或计算方面都会造成潜在的高负担。SDM的一个具有挑战性的应用是边缘计算（edge computing），其中计算和数据存储被推到数据源上。显然，对于任何经典的DP算法来说，边缘的计算能力和存储容量都是非常有限的。更具体地说，本节重点讨论维度诅咒的存储角度。

图7：边缘计算应用。

7.1 近似架构 (Approximation architectures)

总成本函数近似的主要思想是构建一个相对低维的参数化空间来近似总成本函数。具体来说，一个参数化的总成本函数近似器将状态$x\in \mathcal{X}$映射为总成本函数估计值，即。

$$J:\mathcal{X}\times {\mathbb{R}}^m\to \mathbb{R},(x,\theta )\mapsto J(x,\theta )\text{\hspace{1em}(7.1)}$$

其中$\theta$是近似结构的参数（向量）。通过这样的结构，目的是将参数空间的维度从$K$的向量空间减少到$m$的向量空间，$m\ll K$，即减轻维度的诅咒。值得注意的是，实际的总成本函数不一定位于这样的近似空间中。

7.1.1 线性函数近似 （Linear Function Approximation，LFA）

总成本函数近似的一个简单框架是线性函数近似（LFA）。它的目的是构建一组实值特征，这些特征捕捉所有状态的属性，即。

$$\varphi :\mathcal{X}\to {\mathbb{R}}^m,x\mapsto \varphi (x)\text{\hspace{1em}(7.2)}$$

然后将总成本函数近似为这些特征的线性组合，即：
$$J_l:\mathcal{X}\times {\mathbb{R}}^m\to \mathbb{R},(x,\theta )\mapsto {\theta }^{\top }\varphi (x)\text{\hspace{1em}(7.3)}$$

通过将所有特征向量收集到一个矩阵中，即
$$\Phi (x):=\left[\varphi \left(x_1\right),\dots ,\varphi \left(x_K\right)\right]\in {\mathbb{R}}^{m\times K},\text{\hspace{1em}(7.4)}$$

我们可以把近似总成本函数的空间确定为$\Phi (x)$的行的张成，即
$${\mathcal{J}}_l:=\left\{\Phi (x{)}^{\top }h\mid x\in \mathcal{X},h\in {\mathbb{R}}^m\right\}\subset {\mathbb{R}}^K\text{\hspace{1em}(7.5)}$$

当然，假设所有的特征向量都是不同的，所以总成本函数的线性近似仍可区分对于诱导性策略。为了确保每个近似值$J\in {\mathcal{J}}_l$都由$h\in {\mathbb{R}}^m$相对于指定的特征矩阵$\varphi (x)$所代表，线性映射$h\mapsto \Phi (x{)}^{\top }h$需要是单射（一对一映射）。因此，我们假设特征矩阵是满秩的。

Assumption 7.1 特征矩阵的秩

特征矩阵$\Phi (x)\in {\mathbb{R}}^{m\times K}$ 的秩是$m$。

有趣的是，经典的DP算法可以被容易地建模为一个线性总成本函数近似。让我们把表格查询特征（tabular lookup features）定义为
$${\varphi }^{\text{table }}(x):={\left(1_{x_1}(x),\dots ,1_{x_K}(x)\right)}^{\top },\text{\hspace{1em}(7.6)}$$

其中指示函数 1 x i : X → { 0 , 1 } 1_{x_{i}}: \mathcal{X} \rightarrow\{0,1\} 1xi​​:X→{ 0,1} 被定义为
$$1_{x_i}(x):=\{\begin{array}{ll}1,& \text{ if }x=x_i\\ 0,& \text{ otherwise }\end{array}\text{\hspace{1em}(7.7)}$$

尽管MDP的模型假定状态空间的有限性是$\mathrm{D}\mathrm{P}$和RL求解的基础，但许多工程问题并没有这种连续状态空间的便利，如机器人技术。为了使DP或RL方法在解决具有连续状态空间的MDP问题时都是可行的，建立一种构建线性总成本函数近似空间的机制具有很大的实际用途。最流行的技术之一是瓦片编码（tile coding），如图8所示。

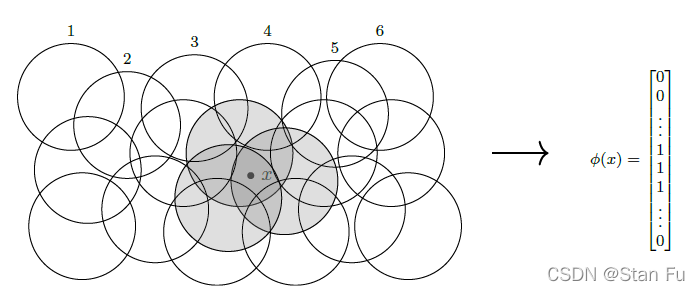
图8：瓦片编码。对于具有连续状态空间的MDP问题，每个圆盘代表一个用于生成特征的局部指标函数。

具体来说，瓦片编码的主要思想是假设相邻的状态具有相同的重要性，因此总成本函数。让我们定义连续状态空间$\mathcal{X}$中的开放子集 ${\mathcal{N}}_k\in \mathcal{X}$, for $k=1,\dots ,\tau$。 我们假设这些开放子集的联合覆盖了状态空间，即。

$$\bigcup _{k=1}^{\tau }{\mathcal{N}}_k=\mathcal{X}\text{\hspace{1em}(7.8)}$$

我们可以定义相同的指示函数为

$$1_{{\mathcal{N}}_i}(x):=\{\begin{array}{ll}1,& \text{ if }x\in {\mathcal{N}}_i\\ 0,& \text{ otherwise }\end{array}$$

然后，可以通过以下方式构建一个瓦片编码特征向量

$${\varphi }^{\text{tile }}(x):={\left(1_{{\mathcal{N}}_1}(x),\dots ,1_{{\mathcal{N}}_{\tau }}(x)\right)}^{\top }.$$

有了线性总成本函数近似的构造，然后就可以直接构造经典的DP算法了。

7.1.2 神经网络函数逼近 (Neural Function Approximation)

深度强化学习（DRL）的最新发展表明，神经网络（NNs）在解决具有大型或连续状态空间的挑战性RL问题方面具有卓越的性能。历史上，神经网络（NN）被用来近似总成本函数已经有几十年了。最近NN在解决模式识别、计算机视觉和语音识别等挑战性问题上的成功，进一步引发了人们对NN应用于总成本函数的努力。基于NN的总成本函数近似（NN-VFA）方法已经在许多具有挑战性的领域中证明了其卓越的性能，例如Atari游戏和围棋游戏。尽管取得了这些进展，对基于NN-VFA的算法的充分理解仍然是一个开放的问题，而且对更具挑战性的应用有着巨大的需求。

一个经典的NN由许多连接的基本计算单元组成，称为神经元，见图9，呈层状结构，如多层感知器（MLP），见图9。

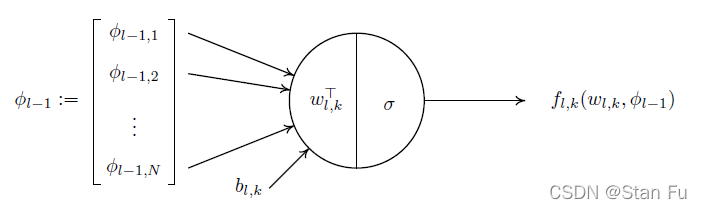
图9：单一感知器神经元的图示。

让$\sigma :\mathbb{R}\to \mathbb{R}$ 是一个单位激活函数，传统上它被选择为非常数、有界、连续和单调增长。常见的例子有Sigmoid函数

$$\sigma (x)=\frac{1}{1+e^{-x}},\text{\hspace{1em}(7.9)}$$

和整流线性单元（ReLU）。

$$\sigma (x)=\{\begin{array}{ll}0,& \text{ for }x\le 0\\ x,& \text{ for }x>0\end{array}\text{\hspace{1em}(7.10)}$$

更确切地说，让我们用$L$表示MLP结构中的层数，用$n_l$表示第$l$层的处理单元数，$l=1,\dots ,L$。 具体来说，用$l=0$，我们指的是输入层，并设定$n_0=K$，$n_L=1$。这里，我们用${\sigma }^{\prime }:\mathbb{R}\to \mathbb{R}$ 是激活函数 $\sigma$ 的一阶导数。

对于MLP结构中的第$(l,k)$个单元，指的是第$l$层中的第$k$个单元，我们定义相应的单元映射为

$$f_{l,k}\left(w_{l,k},{\varphi }_{l-1}\right):=\sigma \left(w_{l,k}^{\top }{\varphi }_{l-1}-b_{l,k}\right),\text{\hspace{1em}(7.11)}$$

其中，${\varphi }_{l-1}\in {\mathbb{R}}^{n_{l-1}}$ 表示来自第$(l-1)$层的输出，$w_{l,k}\in {\mathbb{R}}^{n_{l-1}}$ 和$b_{l,k}\in \mathbb{R}$分别是与第$(l,k)$单元相关的权重向量和偏置。请注意，一般来说，偏差$b_{l,k}$是一个与虚拟单元相关的自由变量。然而，通过下面的分析，为了表述方便，我们把它固定为公式（7.11）中的一个常数标量。然后，我们可以通过堆叠该层的所有单元映射，简单地定义第$l$层映射为

$$f_l\left(W_l,{\varphi }_{l-1}\right):={\left[f_{l,1}\left(w_{l,1},{\varphi }_{l-1}\right),\dots ,f_{l,n_l}\left(w_{l,n_l},{\varphi }_{l-1}\right)\right]}^{\top }\text{\hspace{1em}(7.12)}$$

其中$W_l:=\left[w_{l,1},\dots ,w_{l,n_l}\right]\in {\mathbb{R}}^{n_{l-1}\times n_l}$ 是第$l$个权重矩阵。具体来说，让我们用${\varphi }_0\in {\mathbb{R}}^K$表示输入，那么第$l$层的输出被递归定义为 ${\varphi }_l:=f_l\left(W_l,{\varphi }_{l-1}\right)$ 注意，MLP的最后一层通常采用自映射作为激活函数，即${\varphi }_L:=W_L^{\top }{\varphi }_{L-1}$。最后，用$\mathcal{W}:={\mathbb{R}}^{K\times n_1}\times \dots \times {\mathbb{R}}^{n_{L-1}}$来表示MLP中所有参数矩阵的集合。我们将所有的层间映射组合起来，定义整个MLP网络的映射

$$f:\mathcal{W}\times {\mathbb{R}}^K\to \mathbb{R},(\mathbf{W},x)\mapsto f_L\left(W_L,\cdot \right)\circ \dots \circ f_1\left(W_1,x\right)\text{\hspace{1em}(7.13)}$$

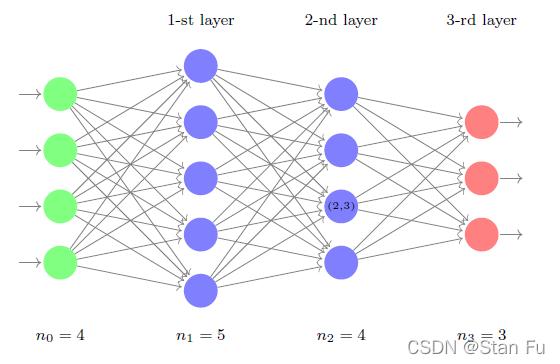
图10：一个有两个隐藏层的MLP。

有了这样的结构，我们可以定义一组参数化的总成本函数，由一个给定的MLP架构规定为
$$\mathcal{F}:=\left\{f(\mathbf{W},\cdot ):{\mathbb{R}}^K\to \mathbb{R}\mid \mathbf{W}\in \mathcal{W}\right\}\text{\hspace{1em}(7.14)}$$

更具体地说，我们用$\mathcal{F}\left(K,n_1,\dots ,n_{L-1},1\right)$来表示MLP的架构，即每层的单元数。让我们用$F_x(\mathbf{W}):=f(\mathbf{W},x)$表示状态为$x$的MLP在$\mathbf{W}$的评估，用$F(x,\mathbf{W}):={\left[F_{x_1}(\mathbf{W}),\dots ,F_{x_K}(\mathbf{W})\right]}^{\top }\in {\mathbb{R}}^K$表示 一个近似的总成本函数，MLP的近似总成本函数集被定义为

J n : = { F ( x , W ) ∣ x ∈ X , W ∈ W } ⊂ R K (7.15) \mathcal{J}_{n}:=\{F(x, \mathbf{W}) \mid x \in \mathcal{X}, \mathbf{W} \in \mathcal{W}\} \subset \mathbb{R}^{K} \tag{7.15} Jn​:={ F(x,W)∣x∈X,W∈W}⊂RK(7.15)

7.2 贝尔曼残差最小化 （Bellman Residual Minimisation ）

对于正在选择的总成本函数的特定近似架构，重要的是调查质量和方法，以确定最佳总成本函数的最佳近似。

定义 7.1 最佳总成本函数的直接估计 (Direct estimate of optimal total cost function).

给定一个无限范围的MDP { X , U , p , g , γ } \{\mathcal{X}, \mathcal{U}, p, g, \gamma\} { X,U,p,g,γ}，和一个封闭子集$\mathcal{J}\subset {\mathbb{R}}^K$，那么最优总成本函数$J_D$的直接最优估计为

$$J_D\in \underset{J\in \mathcal{J}}{\mathrm{argmin}}{\Vert J-J^{\ast }\Vert }_{\infty }\text{\hspace{1em}(7.16)}$$

解决方案$J_D$的质量以其相关GIP的真实总成本来衡量。

Proposition 7.1 最优直接估计的约束

给定一个无限范围的MDP { X , U , p , g , γ } \{\mathcal{X}, \mathcal{U}, p, g, \gamma\} { X,U,p,g,γ}和一个封闭子集$\mathcal{J}\subset {\mathbb{R}}^K$，$J_D\in \mathcal{J}$是$J^{\ast }$的最优直接估计，${\pi }_D$是关于$J_D$的贪婪策略，那么我们有

$${\Vert J^{{\pi }_D}-J^{\ast }\Vert }_{\infty }\le \frac{2(1+\gamma )}{1-\gamma }\underset{J\in \mathcal{J}}{\min }{\Vert J-J^{\ast }\Vert }_{\infty }.\text{\hspace{1em}(7.17)}$$

---

Proof.
通过应用无穷范数的三角不等式，我们可以得到

$$\begin{array}{rl}{\Vert {\mathrm{T}}_{\mathfrak{g}}J-J\Vert }_{\infty }& \le {\Vert {\mathrm{T}}_{\mathfrak{g}}J-J^{\ast }\Vert }_{\infty }+{\Vert J^{\ast }-J\Vert }_{\infty }\\ & \le (1+\gamma ){\Vert J-J^{\ast }\Vert }_{\infty }.\end{array}\text{\hspace{1em}(7.18)}$$

根据 Proposition $4.2$有

$$\begin{array}{rl}{\Vert J^{{\pi }_D}-J^{\ast }\Vert }_{\infty }& \le \frac{2}{1-\gamma }{\Vert {\mathrm{T}}_{\mathfrak{g}}{J}_D-J_D\Vert }_{\infty }\\ & \le \frac{2(1+\gamma )}{1-\gamma }{\Vert J_D-J^{\ast }\Vert }_{\infty }\\ & =\frac{2(1+\gamma )}{1-\gamma }\underset{J\in \mathcal{J}}{\min }{\Vert J-J^{\ast }\Vert }_{\infty }.\end{array}\text{\hspace{1em}(7.19)}$$

即证。

---

很明显，这种对最佳总成本的直接评估只是理论上的讨论。我们需要开发更可行的机制来寻找最佳近似值。定理3.1中所示的最佳贝尔曼算子的充分和必要条件表明，使用最佳贝尔曼算子下的残余误差来估计最佳总成本函数的可能措施如下

定义 7.2 最佳总成本函数的间接估计 (Indirect estimate of optimal total cost function).

给定一个无限范围的MDP $\mathcal{X},\mathcal{U},p,g,\gamma$，和一个封闭子集$\mathcal{J}\subset {\mathbb{R}}^K$，那么最优总成本函数$J_B$的最优间接估计为
$$J_B\in \underset{J\in \mathcal{J}}{\mathrm{argmin}}{\Vert {\mathrm{T}}_{\mathfrak{g}}J-J\Vert }_{\infty }\text{\hspace{1em}(7.20)}$$

注意，$J$与 ${\mathrm{T}}_{\mathfrak{g}}J$之间的差值的最大范数被称为贝尔曼残差（Bellman residual） 。

Proposition 7.2 最优间接估计的约束

给定一个无限范围的MDP { X , U , p , g , γ } \{\mathcal{X}, \mathcal{U}, p, g, \gamma\} { X,U,p,g,γ}，并让$J_B\in \mathcal{J}$是$J^{\ast }$的最优间接估计，${\pi }_B$是关于$J_B$的贪婪策略。那么我们有

$${\Vert J^{{\pi }_B}-J^{\ast }\Vert }_{\infty }\le \frac{2(1+\gamma )}{1-\gamma }\underset{J\in \mathcal{J}}{\min }{\Vert J-J^{\ast }\Vert }_{\infty }.\text{\hspace{1em}(7.21)}$$

---

Proof.
通过应用无穷范数的三角不等式，我们可以得到

$$\begin{array}{rl}{\Vert {\mathrm{T}}_{\mathfrak{g}}J-J\Vert }_{\infty }& \le {\Vert {\mathrm{T}}_{\mathfrak{g}}J-J^{\ast }\Vert }_{\infty }+{\Vert J^{\ast }-J\Vert }_{\infty }\\ & \le (1+\gamma ){\Vert J-J^{\ast }\Vert }_{\infty }.\end{array}\text{\hspace{1em}(7.22)}$$
直接的有
$$\begin{array}{rl}{\Vert {\mathrm{T}}_{\mathfrak{g}}{J}_B-J_B\Vert }_{\infty }& =\underset{J\in \mathcal{J}}{\min }{\Vert {\mathrm{T}}_{\mathfrak{g}}J-J\Vert }_{\infty }\\ & \le (1+\gamma )\underset{J\in \mathcal{J}}{\min }{\Vert J-J^{\ast }\Vert }_{\infty }.\end{array}\text{\hspace{1em}(7.23)}$$

该结果由命题4.2得出。

---

图11：参数化总成本近似的误差界限。

有趣的是，如Propositions 7.1和7.2所示，直接和间接方法所提供的误差界限是相等的。因此，利用贝尔曼残差最小化作为计算工具来估计最优总成本是安全的。另一个有趣的观察表明，只有当最优总成本位于给定的近似集时，两个误差界线才会变成零。显然，来自命题4.3的结果确保了当近似空间被适当构建时，GIP ${\pi }_B$可以是最优的。

Corollary 7.1 最优策略${\pi }_B$的充分不必要约束

给定一个无限范围的MDP $\mathcal{X},\mathcal{U},p,g,\gamma$，并让$J_B\in \mathcal{J}$是$J^{\ast }$的最优间接估计， ${\pi }_B$是关于$J_B$的贪婪策略，最优总成本和任何非最优总成本之间的差距由$\rho :={\min }_{\pi \notin {\mathfrak{P}}_{dm}^{\ast }}{\Vert J^{\pi }-J^{\ast }\Vert }_{\infty }>0$定义。 如果满足以下条件。

$$\underset{J\in \mathcal{J}}{\min }{\Vert J-J^{\ast }\Vert }_{\infty }\le \frac{\rho (1-\gamma )}{2(1+\gamma )}\text{\hspace{1em}(7.24)}$$

那么 ${\pi }_B$ 就是最优的。

7.3 近似价值迭代 （Approximate Value Iteration）

很明显，公式（7.20）中给出的上述贝尔曼残差是很难优化的，特别是由于${\mathrm{T}}_{\mathfrak{g}}$的评估而涉及的离散优化。一个实际的解决方案是采用VI的过程，即在给定的近似架构中对一步最优Bellman算子进行近似评估。

让我们采用线性函数近似架构，让 $J_k={\Phi }^{\top }{\theta }_k$是最佳总成本函数的估计。最佳贝尔曼算子${\mathrm{T}}_{\mathrm{g}}$对$J_k$的一次应用不一定位于同一个子空间$\mathcal{J}$中，如图12所描述。

图12：拟合值迭代算法。从总成本函数$J_k$的第 $k$次估计开始，应用最佳Bellman算子 ${\mathrm{T}}_{\mathfrak{g}}{J}_k$。

为了将其结果${\mathrm{T}}_{\mathfrak{g}}{J}_k$带回$J_k$回到近似空间$\mathcal{J}$，我们需要应用一个与无穷范数相关的适当的正交投影。具体来说，我们有如下更新规则

$$J_{k+1}={\Pi }_{\infty }{\mathrm{T}}_{\mathfrak{g}}{J}_k\text{\hspace{1em}(7.25)}$$

其中${\Pi }_{\infty }$是关于无穷大准则的正交投影

$${\Pi }_{\infty }(J)={\Phi }^{\top }\underset{\theta \in {\mathbb{R}}^m}{\mathrm{argmin}}{\Vert J-{\Phi }^{\top }\theta \Vert }_{\infty }.\text{\hspace{1em}(7.26)}$$

这种投影VI算法被称为拟合VI算法（fitted VI algorithm） 。可以证明，拟合VI收敛到一个唯一的固定点。不幸的是，解决无穷大规范下的最小化问题在数值上是不可行的。为了缓解这种困难，我们可以采用范数的等价性来开发一种数值上可行的算法。

众所周知，对于一个给定的$x\in {\mathbb{R}}^m$，以下关系成立

$$\Vert x{\Vert }_{\infty }\le \Vert x{\Vert }_2\text{\hspace{1em}(7.27)}$$

那么，一个近似的VI步可以被定义为

$$J_{k+1}\in \underset{J\in \mathcal{J}}{\mathrm{argmin}}{\Vert J-{\mathrm{T}}_{\mathfrak{g}}{J}_k\Vert }_2^2.\text{\hspace{1em}(7.28)}$$

由于我们局限于一个LFA架构，所以很容易采用正交投影的解决方案。让我们定义$\Pi :={\Phi }^{\top }{\left(\Phi {\Phi }^{\top }\right)}^{-1}\Phi$，我们可以像Algorithm 9那样直接构建一个具有LFA的近似VI。

需要注意的是，Algorithm 9不能保证收敛性，这是因为组成的操作符$\left(\Pi T_{\mathfrak{g}}\right):{\mathbb{R}}^K\to {\mathbb{R}}^K$对于$|\cdot {\Vert }_2$或$|\cdot {\Vert }_{\infty }$来说都不是一个收缩。这种现象在近似DP的背景下被称为范数不匹配(norm mismatch) 。

在本节的其余部分，我们研究近似VI的通用框架的收敛性。对于一个给定的估计值$J_k$，一个近似的VI步骤被计算为找到一个新的估计值，但要达到一定的误差，如下面的不等式，并对所有$k=0,1,\dots ,\infty$ 进行计算

$${\Vert J_{k+1}-{\mathrm{T}}_{\mathfrak{g}}{J}_k\Vert }_{\infty }\le \delta .\text{\hspace{1em}(7.29)}$$

在这里，可以用范数之间的等价关系来指定误差界限$\delta$，即：

$${\Vert J_{k+1}-{\mathrm{T}}_{\mathfrak{g}}{J}_k\Vert }_{\infty }\le {\Vert J_{k+1}-{\mathrm{T}}_{\mathfrak{g}}{J}_k\Vert }_2.\text{\hspace{1em}(7.30)}$$

图13说明了一个通用AVI算法的基本思路。

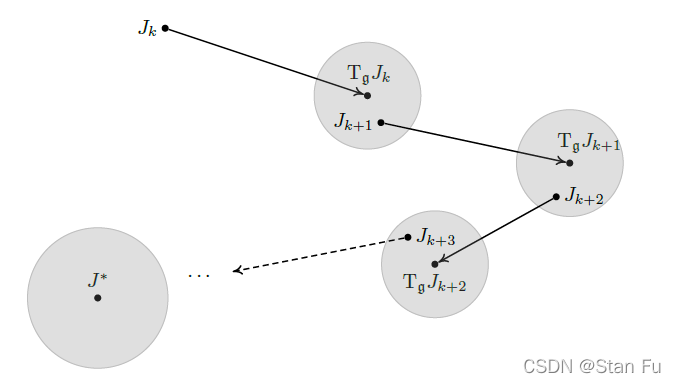
图13：近似值迭代算法。这里，总成本函数估计值周围的每个圆盘象征着总成本函数近似的误差容限。

在下面的Proposition 中，我们从估计值和最佳总成本函数之间的误差或差异方面来研究其性能。

Proposition 7.3 近似VI算法的误差界限 (Error bounds for approximate VI algorithm)

给定一个无限范围的MDP { X , U , p , g , γ } \{\mathcal{X}, \mathcal{U}, p, g, \gamma\} { X,U,p,g,γ}，由近似$VI$算法产生的$J_k$序列满足以下不等式

$$\underset{k\to \infty }{\lim }{\Vert J_k-J^{\ast }\Vert }_{\infty }\le \frac{\delta }{1-\gamma }\text{\hspace{1em}(7.31)}$$

---

Proof.

定义$J_0\in {\mathbb{R}}^K$ 是总成本函数的初始估计。我们可以将无穷范数的三角形不等式应用于近似VI的第$k$输出与精确VI算子的第$k$输出之间的差值，如下所示

$$\begin{array}{rl}{\Vert J_k-{\mathrm{T}}_{\mathfrak{g}}^k{J}_0\Vert }_{\infty }=& \Vert J_k-{\mathrm{T}}_{\mathfrak{g}}{J}_{k-1}+{\mathrm{T}}_{\mathfrak{g}}{J}_{k-1}-{\mathrm{T}}_{\mathfrak{g}}^2{J}_{k-2}+\dots \\ & \dots -{\mathrm{T}}_{\mathfrak{g}}^{k-1}{J}_1+{\mathrm{T}}_{\mathfrak{g}}^{k-1}{J}_1-{\mathrm{T}}_{\mathfrak{g}}^k{J}_0{\Vert }_{\infty }\\ \le & {\Vert J_k-{\mathrm{T}}_{\mathfrak{g}}{J}_{k-1}\Vert }_{\infty }+{\Vert {\mathrm{T}}_{\mathfrak{g}}{J}_{k-1}-{\mathrm{T}}_{\mathfrak{g}}^2{J}_{k-2}\Vert }_{\infty }+{\Vert {\mathrm{T}}_{\mathfrak{g}}^{k-1}{J}_1-{\mathrm{T}}_{\mathfrak{g}}^k{J}_0\Vert }_{\infty }\\ \le & \delta +\gamma \delta +\dots +{\gamma }^{k-1}\delta ,\end{array}\text{\hspace{1em}(7.32)}$$

其中第二个不等式是由于最佳贝尔曼算子的收缩特性${\mathrm{T}}_{\mathfrak{g}}$。根据几何级数的特性，我们得到

$${\Vert J_k-{\mathrm{T}}_{\mathfrak{g}}^k{J}_0\Vert }_{\infty }\le \frac{1-{\gamma }^k}{1-\gamma }\delta \text{\hspace{1em}(7.33)}$$

让极限$k\to \infty$，结果由Proposition 3.5中的VI算法的收敛性得出，即${\lim }_{k\to \infty }{\mathrm{T}}_{\mathfrak{g}}^k{J}_0=J^{\ast }$。

---

与经典的VI算法类似，就近似VI算法产生的估计总成本函数而言，可以一系列贪婪诱导性策略。通过回顾Theorem 4.1中GIP的直接误差界限，我们直接得出以下属性

$$\begin{array}{rl}\underset{k\to \infty }{\lim }{\Vert J^{{\pi }_k}-J^{\ast }\Vert }_{\infty }& \le \frac{2\gamma }{1-\gamma }\underset{k\to \infty }{\lim }{\Vert J_k-J^{\ast }\Vert }_{\infty }\\ & \le \frac{2\gamma \delta }{(1-\gamma {)}^2}\end{array}\text{\hspace{1em}(7.34)}$$

其中$J^{{\pi }_k}$是相对于近似VI算法的第$k$次迭代的GIP。

Corollary 7.2 一般AVI算法的有界性

给定一个无限范围的MDP { X , U , p , g , γ } \{\mathcal{X}, \mathcal{U}, p, g, \gamma\} { X,U,p,g,γ}，让$J_k$ 是由近似VI算法产生的总成本函数估计序列。让我们用${\pi }_k$表示关于$J_k$的相应的贪婪诱导策略，那么GIP的总成本函数${\pi }_k$满足以下属性

$$\underset{k\to \infty }{\lim }{\Vert J^{{\pi }_k}-J^{\ast }\Vert }_{\infty }\le \frac{2\gamma \delta }{(1-\gamma {)}^2}\text{\hspace{1em}(7.35)}$$

Remark 7.1 公差$\delta$与误差$\rho$的关系

正如我们已经讨论过的，上述误差界限可以是保守的。为了能够从AVI算法的结果中检索出一个最优策略，我们回顾一下命题4.3的结果。设$\rho >0$为最佳总成本函数和其最接近的总成本函数之间的误差，如公式（4.11）所定义。预计AVI算法极限处的误差界限将服从以下不等式

$$\underset{k\to \infty }{\lim }{\Vert J_k-J^{\ast }\Vert }_{\infty }\le \frac{\delta }{1-\gamma }<\frac{\rho (1-\gamma )}{2\gamma }\text{\hspace{1em}(7.36)}$$

作为结果，我们有

$$\delta <\frac{\rho (1-\gamma {)}^2}{2\gamma }\text{\hspace{1em}(7.37)}$$

显然，公差$\delta$的选择取决于$\rho$的总成本，不幸的是，这在一般情况下是无法获得的。

7.3 Example: E-Bus

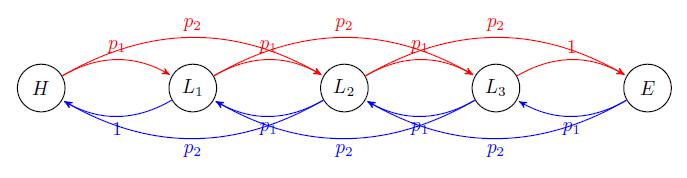
Consider a group of electric buses running round trips 24 hours a day. The task is to identify optimal operating actions at different battery states. The battery’s endurance and charging speed gradually decrease with the increase of battery life. Hence, for different buses, they have different transition probabilities between battery states. The following figure illustrates the state transitions between different states.

• Five states: $H$ - high battery, $E$ - empty battery, $L_1,L_2,L_3$ : three different low level battery statuses
• Two actions: $S$- continue to serve, C - charge
• Numbers on the edges refer to transition probabilities. $p_1=0.4,p_2=0.6$
• Discount factor $\gamma =0.9$ .

We choose the number of unserviced passengers as the local costs:

• In the high battery state, if it keeps the service, the unserviced passenger number is 0 .
• In all the low battery stats, if it keeps the service, the unserviced passenger number is 2 .
• In all the low battery state and empty battery, if it charges the battery, the unserviced passenger number is 5 .

Task 1: Implement Value Iteration (VI) and Approximate Value Iteration (AVI) algorithm with Linear Function approximation (LFA) using the feature matrix

$$\Phi =\left[\begin{array}{ccccc}-0.40& -0.44& -0.45& -0.46& -0.48\\ -0.07& 0.73& -0.61& 0.21& -0.23\end{array}\right]$$

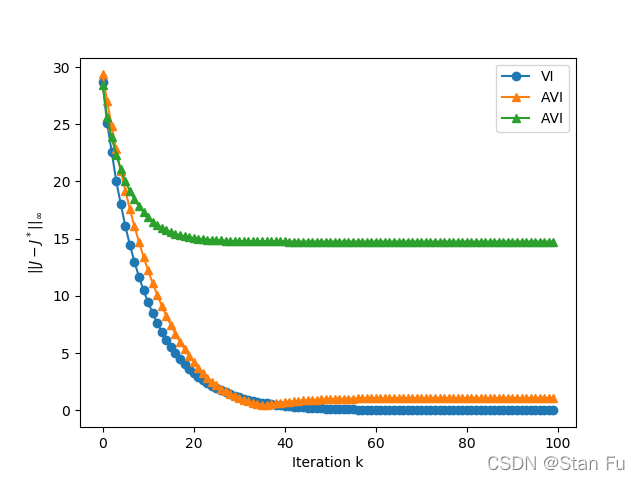
Compare their convergence speeds in terms of the difference from each iterate to the corresponding accumulation point ${\Vert J_k-J^{\ast }\Vert }_{\infty }$ against the index of sweep $k$ .

Task 2: Given the gap between the optimal total cost and any non-optimal total cost ($\rho :={\min }_{\pi \notin {\mathfrak{P}}_{dm}^{\ast }}{\Vert J^{\pi }-J^{\ast }\Vert }_{\infty }=0.239$ ), check conditions on optimality in policy according to Eq. (7.24).

Task 3: If we use a random-generated feature matrix $\Phi$ , repeat the aforementioned two tasks, what can we observe? Discussion: how do we choose the feature matrix $\Phi$ .

7.3.1 相关代码

import random
import matplotlib.pyplot as plt
import matplotlib
import numpy as np

matplotlib.rcParams.update(matplotlib.rcParamsDefault)

INIT_J = 0  # define initial total cost
ITER_N = 100  # the number of iterations

# transition probability
p1 = 0.4
p2 = 0.6

# cost of each state-action pair
ghs = 0
gl1s = gl2s = gl3s = 2
gec = gl3c = gl2c = gl1c = 5

# discount factor
gamma = 0.9

##
# using VI to get optimal_J. i.e. J*:
k = 0
jh = jl1 = jl2 = jl3 = je = INIT_J
while k < 200:
    jh_ = p1 * (ghs + gamma * jl1) + p2 * (ghs + gamma * jl2)
    jl1_ = min(p1 * (gl1s + gamma * jl2) + p2 * (gl1s + gamma * jl3), gl1c + gamma * jh)
    jl2_ = min(p1 * (gl2s + gamma * jl3) + p2 * (gl2s + gamma * je),
               p1 * (gl2c + gamma * jl1) + p2 * (gl2c + gamma * jh))
    jl3_ = min(gl3s + gamma * je, p1 * (gl3c + gamma * jl2) + p2 * (gl3c + gamma * jl1))
    je_ = p1 * (gec + gamma * jl3) + p2 * (gec + gamma * jl2)

    jh, jl1, jl2, jl3, je = jh_, jl1_, jl2_, jl3_, je_
    k += 1

jh_optim, jl1_optim, jl2_optim, jl3_optim, je_optim = jh, jl1, jl2, jl3, je
print('After VI we get the optimal costs {:.4f} {:.4f} {:.4f} {:.4f} {:.4f}'.format(jh_optim, jl1_optim, jl2_optim,
                                                                                    jl3_optim, je_optim))


##
# VI
jh = jl1 = jl2 = jl3 = je = INIT_J
vi_converge = []

for k in range(ITER_N):
    jh_ = p1 * (ghs + gamma * jl1) + p2 * (ghs + gamma * jl2)
    jl1_ = min(p1 * (gl1s + gamma * jl2) + p2 * (gl1s + gamma * jl3), gl1c + gamma * jh)
    jl2_ = min(p1 * (gl2s + gamma * jl3) + p2 * (gl2s + gamma * je),
               p1 * (gl2c + gamma * jl1) + p2 * (gl2c + gamma * jh))
    jl3_ = min(gl3s + gamma * je, p1 * (gl3c + gamma * jl2) + p2 * (gl3c + gamma * jl1))
    je_ = p1 * (gec + gamma * jl3) + p2 * (gec + gamma * jl2)

    jh, jl1, jl2, jl3, je = jh_, jl1_, jl2_, jl3_, je_
    k += 1
    # calculate the infinite norm of ||J_k - J*||
    infinity_gap = max(
        abs(jh - jh_optim),
        abs(jl1 - jl1_optim),
        abs(jl2 - jl2_optim),
        abs(jl3 - jl3_optim),
        abs(je - je_optim)
    )
    vi_converge.append(infinity_gap)

plt.plot(range(ITER_N), vi_converge, 'o-', label='VI')

plt.ylabel(r"$\|\| J - J^*\|\|_{\infty}$")
plt.xlabel('Iteration k')

##
# Approximate value iteration using specific features

phi = np.array([[-0.4, -0.44, -0.45, -0.46, -0.48],
                [-0.07, 0.73, -0.61, 0.21, -0.23]])
inv = np.linalg.inv(phi @ phi.T)
PI = phi.T @ inv @ phi
# boundary of optimal indirect estimate
rho = 0.239
boundary = rho * (1 - gamma) / (2 * (1 + gamma))
print('Upper bound  = {}, '.format(boundary))

J_AVI = np.array([0, 0, 0, 0, 0])
J_OPT = np.array([jh_optim, jl1_optim, jl2_optim, jl3_optim, je_optim])
print('\t and the left hand side = {}'.format(min(abs(PI @ J_OPT - J_OPT))))
avi_converge = []
for k in range(ITER_N):
    # TgJk
    jh, jl1, jl2, jl3, je = J_AVI
    jh_ = p1 * (ghs + gamma * jl1) + p2 * (ghs + gamma * jl2)
    jl1_ = min(p1 * (gl1s + gamma * jl2) + p2 * (gl1s + gamma * jl3), gl1c + gamma * jh)
    jl2_ = min(p1 * (gl2s + gamma * jl3) + p2 * (gl2s + gamma * je),
               p1 * (gl2c + gamma * jl1) + p2 * (gl2c + gamma * jh))
    jl3_ = min(gl3s + gamma * je, p1 * (gl3c + gamma * jl2) + p2 * (gl3c + gamma * jl1))
    je_ = p1 * (gec + gamma * jl3) + p2 * (gec + gamma * jl2)
    J_AVI = np.array([jh_, jl1_, jl2_, jl3_, je_])

    # orthogonal projector
    J_AVI = PI @ J_AVI
    if min(abs(J_AVI - J_OPT)) <= boundary:
        print('After {} iterations, the policy is optimal'.format(k))
    avi_converge.append(max(abs(J_AVI - J_OPT)))

plt.plot(range(ITER_N), avi_converge, '^-', label='AVI')

##
# Approximate value iteration using random features

phi = np.random.rand(2, 5)
inv = np.linalg.inv(phi @ phi.T)
PI = phi.T @ inv @ phi
# boundary of optimal indirect estimate
rho = 0.239
boundary = rho * (1 - gamma) / 2 * (1 + gamma)

J_AVI_rand = np.array([0, 0, 0, 0, 0])
avi_converge_rand = []
for k in range(ITER_N):
    # TgJk
    jh, jl1, jl2, jl3, je = J_AVI_rand
    jh_ = p1 * (ghs + gamma * jl1) + p2 * (ghs + gamma * jl2)
    jl1_ = min(p1 * (gl1s + gamma * jl2) + p2 * (gl1s + gamma * jl3), gl1c + gamma * jh)
    jl2_ = min(p1 * (gl2s + gamma * jl3) + p2 * (gl2s + gamma * je),
               p1 * (gl2c + gamma * jl1) + p2 * (gl2c + gamma * jh))
    jl3_ = min(gl3s + gamma * je, p1 * (gl3c + gamma * jl2) + p2 * (gl3c + gamma * jl1))
    je_ = p1 * (gec + gamma * jl3) + p2 * (gec + gamma * jl2)
    J_AVI_rand = np.array([jh_, jl1_, jl2_, jl3_, je_])

    # orthogonal projector
    J_AVI_rand = PI @ J_AVI_rand
    if min(abs(J_AVI_rand - J_OPT)) <= boundary:
        print('After {} iterations, the policy is optimal'.format(k))
    avi_converge_rand.append(max(abs(J_AVI_rand - J_OPT)))

plt.plot(range(ITER_N), avi_converge_rand, '^-', label='AVI')


plt.legend()
plt.show()

7.3.2 输出结果

After VI we get the optimal costs 26.1268 28.5141 29.3736 30.7331 31.9256
Upper bound  = 0.006289473684210525, 
	 and the left hand side = 0.20402763408068125
After 44 iterations, the policy is optimal

7.3.3 Feature matrix $\Phi$

• Calculate $J^{\pi }$ for all the possible policies. $J^{\pi }\in {\mathbb{R}}^{8\times 5}$
  So, how to establish a $J^{\pi }$ for all the possible policies?
• Singular value decomposition (SVD): $J^{\pi }={\mathbf{U}\mathbf{\Sigma }\mathbf{V}}^{\ast }$.
• Select the first two component of ${\mathbf{V}}^{\ast }$ as $\Phi$