图的定义
· 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示
为:G(V,E)。其中G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
-在图中数据元素称之为顶点(Vertex)。
-顶点集合要有穷非空。
-任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以空。
· 无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边(Egde),
用无序偶(Vi,Vj)来表示。
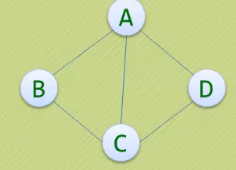
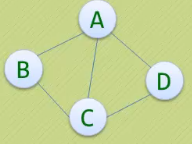
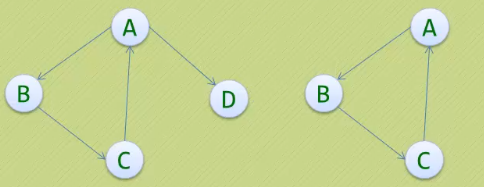
· 上图G1是一个无向图,G1={V1,E1},其中
-V1={A,B,C,D},

-E1={(A,B),(B,C),(C,D),(D,A),(A,C)}
· 有向边:若从顶点Vi到Vj的边有方向,则称这条边为有向边,也成为弧(Arc),
用有序偶<Vi,Vj>来表示,Vi称为弧尾,Vj称为弧头。
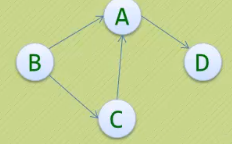
· 上图G2是一个有向图,G2={V2,E2},其中
-V2={A,B,C,D}
-E2={<B,A>,<B,C>,<C,A>,<A,D>}
· 简单图:在图结构中,若不存在顶点到其自身的边,且同一条边不重复
出现 ,则称这样的图为简单图。
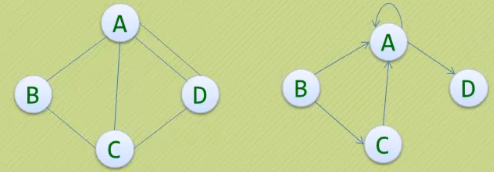
· 以下两个则不属于简单图:
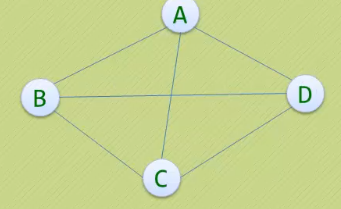
· 无向完全图:在无向完全图中,如果任意两个顶点之间都存在边,则称
该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2条边。
· 有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的
两天弧,则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边。
· 稀疏图和稠密图:这里的稀疏和稠密是模糊的概念,都是相对而言,通常认为边或
弧数小于n*logn(n是顶点的个数)的图称为稀疏图,反之称为稠密图。
· 有些图的边或弧带有与它相关的数字,这种与图的边或弧相关的数叫做权(Weight),
带权的图通常称为网(Network)。
· 假设有两个图G1=(V1,E1)和G2=(V2,E2),如果V2属于V1,E2属于E1,则
称G2为G1的子图(Subgraph)。
图的顶点与边之间的关系
· 对于无向图G=(V,E),如果边(V1,V2)属于E,则称顶点V1和V2互为邻接点(Adjacent),即V1和V2相
邻接。边(V1,V2)依附(incident)于顶点V1和V2,或者说(V1,V2)与顶点V1和V2相关联。
· 顶点V的度(Degree)是和V相关联的边的数目,记为TD(V),如下图,顶点A与B互为邻接点,
边(A,B)依附于顶点A与B上,顶点A的度为3。
· 对于有向图G=(V,E),如果有<V1,V2>属于E,则称顶点V1邻接到顶点V2,顶点V2邻接自顶点V1。
· 以顶点V为头的弧的数目称为V的入度(InDegree),记为ID(V),以V为尾的弧的数目称为
V的出度(OutDegree),记为OD(V),因此顶点V的度为TD(V)=ID(V)+OD(V)
· 下图顶点A的入度是2,出度是1,所以顶点A的度是3。
路径
· 无向图G=(V,E)中从顶点V1到顶点V2的路径。
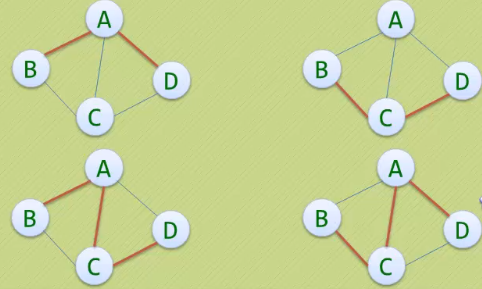
· 下图用红线列举了从顶点B到顶点D的四种不同路径:
· 如果G是有向图,则路径也是有向的。
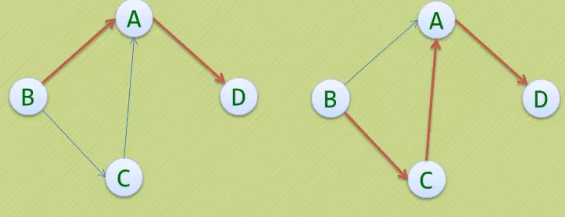
· 下图用红线列举顶点B到顶点D的两种路径,而顶点A到顶点B就不存在路径:
· 路径的长度是路径上的边或弧的数目。
· 第一个顶点到最后一个顶点相同的路径称为回路或者环(Cycle)。
· 序列中顶点不重复出现的路径称为 简单路径,除了第一个顶点和最后一个顶点
之外,其余顶点不重复出现的回路,称为简单回炉或简单环。
· 下图左侧是简单环,右侧 不是简单环:
连通图
· 在无向图G中,如果匆匆顶点V1到顶点V2有路径,则称V1和V2是联通的,如果
对于图中任意两个顶点Vi和Vj都是连通的,则称G是连通图。
· 无向图中的极大连通子图称为连通分量。
· 注意以下概念:
-首先要是子图,并且子图是要连通的。
-连通子图含有极大顶点数。
-具有极大顶点数的连通子图包含依附于这些顶点的所有边。
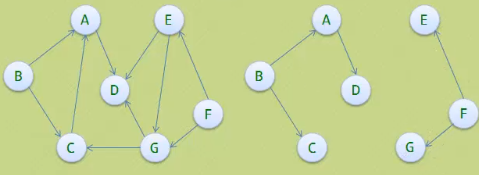
· 在有向图G中,如果对于每一队Vi到Vj都存在路径,则称G是强连通图。
· 有向图中的极大强连通子图称为有向图的强连通分量。
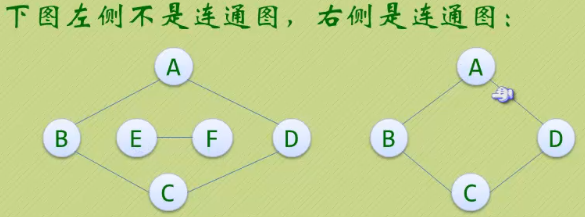
· 下图左侧并不是强连通图,右侧是。并且右侧是左侧的极大强连通子图,
也是左侧的强连通分量。
· 最后我们再来看连通图的生成树定义。
· 所谓的一个连通图的生成树是一个极小的连通子图,它含有图中全部的n个
顶点,但只有足以构成一棵树的n-1条边。
· 如果一个有向图恰有一个顶点入度为0,其余顶点入度均为1,则是一棵有向树。
左边的有向图,能拆分成右边两棵有向树。
图的存储结构
· 因为任意两个顶点之间都可能村长联系,因此无法以数据元素在内存中的物理
位置来表示元素之间的关系(内存物理位置是线性的,图的元素关系是平面的)。
· 如果用多重链表来描述倒是可以做到,但是纯粹用多重链表导致的浪费是无法
想象的(如果各个顶点的度数相差太大,就会造成巨大的浪费)。
邻接矩阵(无向图)
· 考虑到图是由顶点和边或弧两部分组成,自然会用到两个结构体来存储。
· 顶点因为不区分大小、主次,所以用一个一维数组来存储。
· 边或弧由于是顶点与顶点之间的关系,可以考虑二维数组来存储。
· 图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点
信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
· vertex[4]={v0,v1,v2,v3},边数组arc[4][4]为对称矩阵(由于无向图不分先后)
0表示不存在顶点间的边,1表示顶点间存在边。
· 对称矩阵:所谓对称矩阵就是n阶矩阵的元满足a[i][j]=a[j][i](0<=i,j<=n)。
· 有了这个二维数组组成的对称矩阵,可以很容易地知道图中的信息:
-要判定任意两顶点是否有边无边就非常容易。
-某个顶点的度就为这个顶点Vi在邻接矩阵中第i行(列)的元素之和。
-顶点Vi的所有邻接点就是矩阵中第i行元素扫描一遍,为1就是邻接点。
邻接矩阵(有向图)
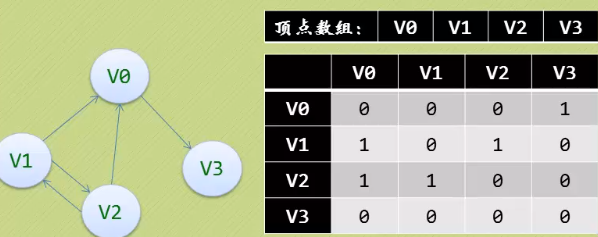
· 可见顶点数组vertex[4]={V0,V1,V2,V3},弧树组arc[4][4]也是一个矩阵,但因为是有
向图,所以这个矩阵并不对称,例如由V1到V0有弧,得到arc[1][0]=1,而V0到V1
没有弧,因此arc[0][1]=0。
· 关于入度和出度,顶点V1的入度为1,整合是第V1列各数之和,
顶点V1的出度为2,正好是第V1行的各数之和。
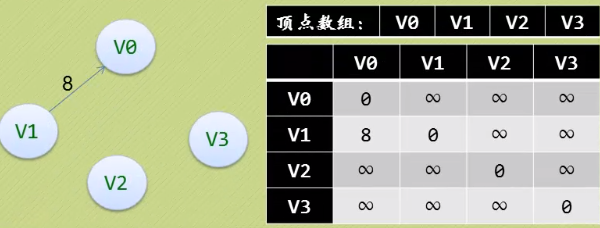
邻接矩阵(网)
· 当i=j时书上是用∞表示,有的地方用0表示
· 这里“∞”表示一个计算机允许的,大于所有边上权值的值(int最大值65535)。
图的数组表示法,结构体:
#define INFINITY 65535 //表示无穷大-->在带权的图中用到,即网
#define MAX_VERTEX_NUM 20 //图的最大顶点数
#define MAX_INFO 20 //最大信息数
typedef char InfoType; //附加信息类型
typedef int VRType; //顶点关系类型
typedef int VertexType; //顶点数据类型
//图的种类:有向图,有向网,无向图,无向网
typedef enum {
DG, DN, UDG, UDN
} GraphKind;
typedef struct ArcCell {
VRType adj; //顶点关系类型,对无权图用1或0表示是否相邻
//对带权图,则为权值类型
InfoType *info; //附加信息指针
} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct {
VertexType vexs[MAX_VERTEX_NUM];//顶点向量
AdjMatrix arcs; //邻接矩阵
int vexnum, arcnum; //当前顶点数和弧数
GraphKind kind; //图的种类
} MGraph;
邻接表(无向图)
· 我们可以发现,对于边数相对较少的图,上面的邻接矩阵是存在巨大浪费的。如下图
· 因此可以采用数组和链表组合起来存储,这里称为邻接表。
· 邻接表的处理方法是这样的:
-图中顶点用一个一维数组存储。
-图中每个顶点Vi的所有邻接点构成一个线性表,由于个数不确定,所以用单链表存储。
邻接表(有向图)
· 类似地,下面是把顶点当弧尾建立的邻接表,这样容易得到每个顶点的出度。
· 有时为了确定顶点的入度或以顶点为弧头的弧,可以建立一个有向图的逆邻接表。
邻接表(网)
· 对于带权值的网图,可以在边表结点定义中再增加一个数据域来存储权值即可。
图的邻接表存储,结构体:
#define MAX_VERTEX_NUM 20
typedef char InfoType; //附加信息类型
typedef int VertexType; //顶点数据类型
typedef struct ArcNode{
int adjvex; //该弧所指向的顶点位置
struct ArcNode *nextarc;//下个结点
InfoType *info; //当前结点(弧)的信息
}ArcNode;
typedef struct VNode{
VertexType data;//顶点信息
ArcNode *firstarc;//指向第一个依附于该顶点弧的指针
}VNode,*AdjList[MAX_VERTEX_NUM];
typedef struct {
AdjList vertices;
int vexnum,arcnum;//图的当前顶点数和弧数
int kind; //图的种类标志
}ALGraph;
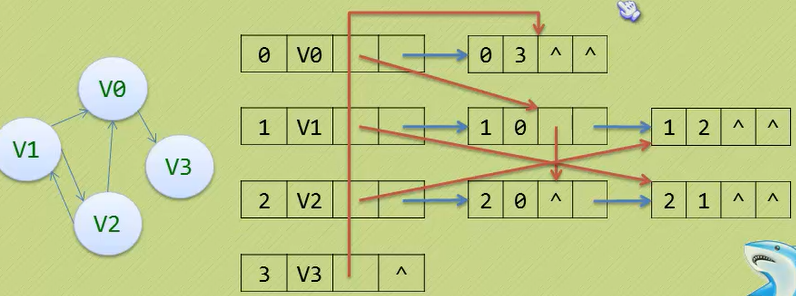
十字链表(是对于有向图来说的,关心出入度问题,所以把两个邻接表结合一起)
· 邻接表固然优秀,但也有不足,例如对有向图的处理上,有时需要再建立一个逆邻接表。
· 这时候就出现了十字链表。
· 为此重新定义顶点表结构结点结构:
· 接着重新定义边表结点结构:
· 可以发现,蓝线是邻接表的指向,红线是逆邻接表的指向,是把他们合起来了。
· 十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到Vi为
尾的弧,也容易找到以Vi为头的弧,因而容易求得顶点的出度和入度。
· 十字链表除了结构复杂一点外,其实创建图算法的时间复杂度是和邻接表相同的。
因此,在有向图的应用中,十字链表也是非常好的数据结构模型。
//十字链表
#define MAX_VERTEX_NUM 20
typedef char InfoType; //附加信息类型
typedef int VertexType; //顶点数据类型
typedef struct ArcBox{
int tailvex,headvex; //该弧的尾和头顶点的位置
struct ArcBox *hlink,*tlink;//分别为弧头相同回合弧尾相同的弧的链域
InfoType *info; //该弧相关信息的指针
}ArcBox;
typedef struct VexNode{
VertexType data;
ArcBox *firstin,*firstout;//分别指向该顶点第一条弧和出弧
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM];//表头向量
int vexnum,arcnum; //有向图的当前顶点数和弧数
}OLGraph;
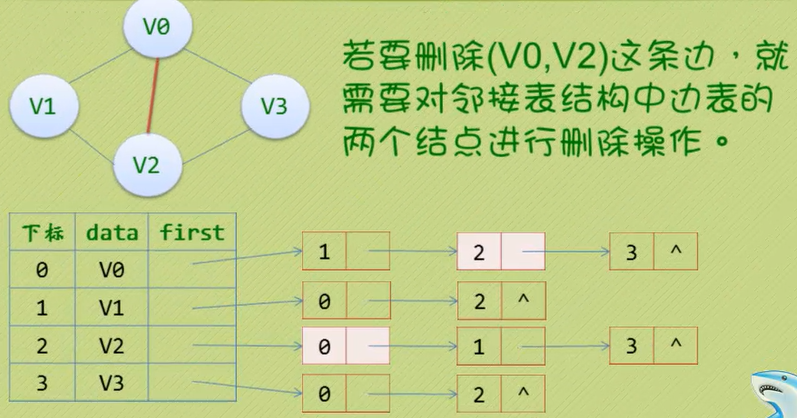
邻接多重表(对无向图而言)
· 如果在无向图的应用中,关注的重点是顶点的话,那么邻接表是不错的选择,但如果更挂关注的是边的操作,
比如对已经访问过的边做标记,或者删除某一条边等操作,邻接表就显得不方便了(如下图)
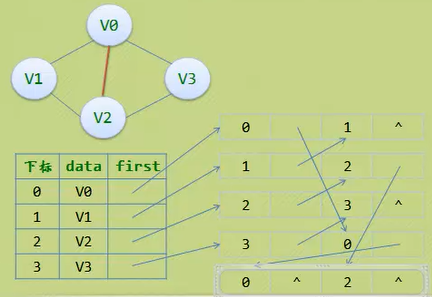
· 因此,这里仿造十字链表的方式,对边表结构进行改装,重新定义的边表结构如下:
· 其中iVex和jVex是与某条边依附的两个顶点在顶点表中的下标。
iLink指向依附点iVex的下一条边,jLink指向依附顶点jVex的下一条边。
· 也就是说在邻接多重表里边,边表存放的是一条边,而不是一个顶点。
//无向图的邻接多重表存储结构
#define MAX_VERTEX_NUM 20
typedef char InfoType; //附加信息类型
typedef int VertexType; //顶点数据类型
typedef enum {unvisited,visited}VisitIf;
typedef struct EBox{
VisitIf mark; //访问标记
int ivex,jvex; //该边依附的两个顶点的位置
struct EBox *ilink,*jlink;//分别指向依附这两个顶点的下一条边
InfoType *info; //该边信息指针
}EBox;
typedef struct VexBox{
VertexType data;
EBox *firstedge;//指向第一条依附该顶点的边
}VexBox;
typedef struct {
VexBox adjmulist[MAX_VERTEX_NUM];
int vexnum,edgenum;//无向图的当前顶点数和边数
}AMLGraph;
图的遍历(这里以邻接矩阵表示)
· 对于图的遍历,因为它的任一顶点都可以和其余的所有顶点相邻接,
因此极有可能村长重复走过某个顶点或漏了某个顶点的遍历过程。
· 如果要避免这种情况,就需要合理科学地遍历,常见的有两种遍历:
深度优先遍历和广度优先遍历。
深度优先遍历
· 也称为深度优先搜索,简称为DFS。
· 从图的某一点按照某个原则进行深度遍历,把遍历过的点作一个标记,在一个分支上
遍历到底后,逐个顶点退回,遍历其他分支,直到退回到原点,遍历完毕。
· 类似于树的先根遍历,是树的先根遍历的推广。
假设先从A遍历
代码实现:
int FirstAdjVex(MGraph G, int v) {
//返回v(序号)的第一个相邻节点(序号)
if (v > G.vexnum || v < 0)
return -1;
int i, j;
j = 0;
//如果是网
if (G.kind == DN || G.kind == UDN)
j = INFINITY;
for (i = 0; i < G.vexnum; i++)
if (G.arcs[v][i].adj != j)
return i;
return -1;
}
int NextAdjVex(MGraph G, int v, int w) {
//w是v的相邻节点,返回v相对w的下一个节点的序号,否则返回-1
int i, j;
j = 0;
//如果为网
if (G.kind == DN || G.kind == UDN)
j = INFINITY;
//两顶点不相邻
if (G.arcs[v][w].adj == j)
return -1;
//从w之后的结点开始
for (i = w + 1; i < G.vexnum; i++)
if (G.arcs[v][i].adj != j)
return i;
return -1;
}
int visited[MAX_VERTEX_NUM];//访问标记数组
void DFS(MGraph G, int v) {
//从第v个顶点出发递归地深度优先遍历图G
visited[v] = 1;
printf("%d", G.vexs[v]);//访问第v个顶点
for (int w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w))
if (!visited[w])//对未访问的邻接顶点w递归调用DFS
DFS(G, w);
}
void DFSTraverse(MGraph G) {
for (int i = 0; i < G.vexnum; ++i) {
visited[i] = 0; //访问标志数组初始化
}
for (int j = 0; j < G.vexnum; ++j) {
if (!visited[j])
DFS(G, j); //对未访问的顶点调用DFS
}
}
int main() {
MGraph G;
CreateGraph(G);
DFSTraverse(G);
return 0;
}
广度优先遍历
· 又称为广度优先搜索,简称BFS。
· 要实现广度优先遍历,可以利用队列来实现。
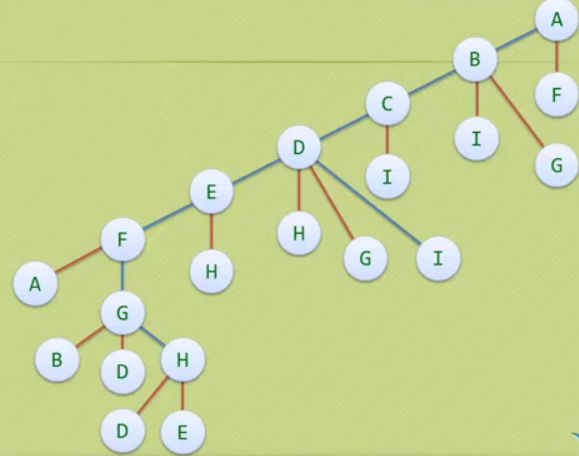
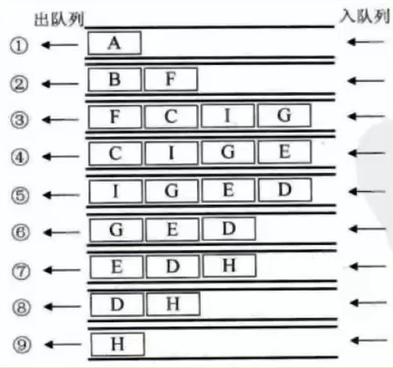
· 访问A后,把与A相邻的结点入队列,A标记已入过列。访问B,把B相邻的C,I,G入列
并标记已入列。访问F,把F相邻的G,E入列,因为G已被标记,所以只要E入列,依次类推。
代码实现:
void BFSTraverse(MGraph G) {
//按广度优先非递归遍历图G,使用辅助队列Q和访问标志数组visited
int v, w;
VertexType u;
LinkQueue Q;
for (v = 0; v < G.vexnum; ++v)//标志数组初始化
visited[v] = 0;
IniteQueue(Q); //生成队列
for (v = 0; v < G.vexnum; ++v)
if (!visited[v]) {
visited[v] = 1;
printf("%d", G.vexs[v]);
EnQueue(Q, v); //v入队列
while (!QueueEmpty(Q)) {
DeQueue(Q, u); //队头元素出队并至为u
for (w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w))
if (!visited[w]) { //w为u的尚未访问的邻接点
visited[w] = 1;
printf("%d", G.vexs[w]);
EnQueue(Q, w);
}
}
}
}
最小生成树
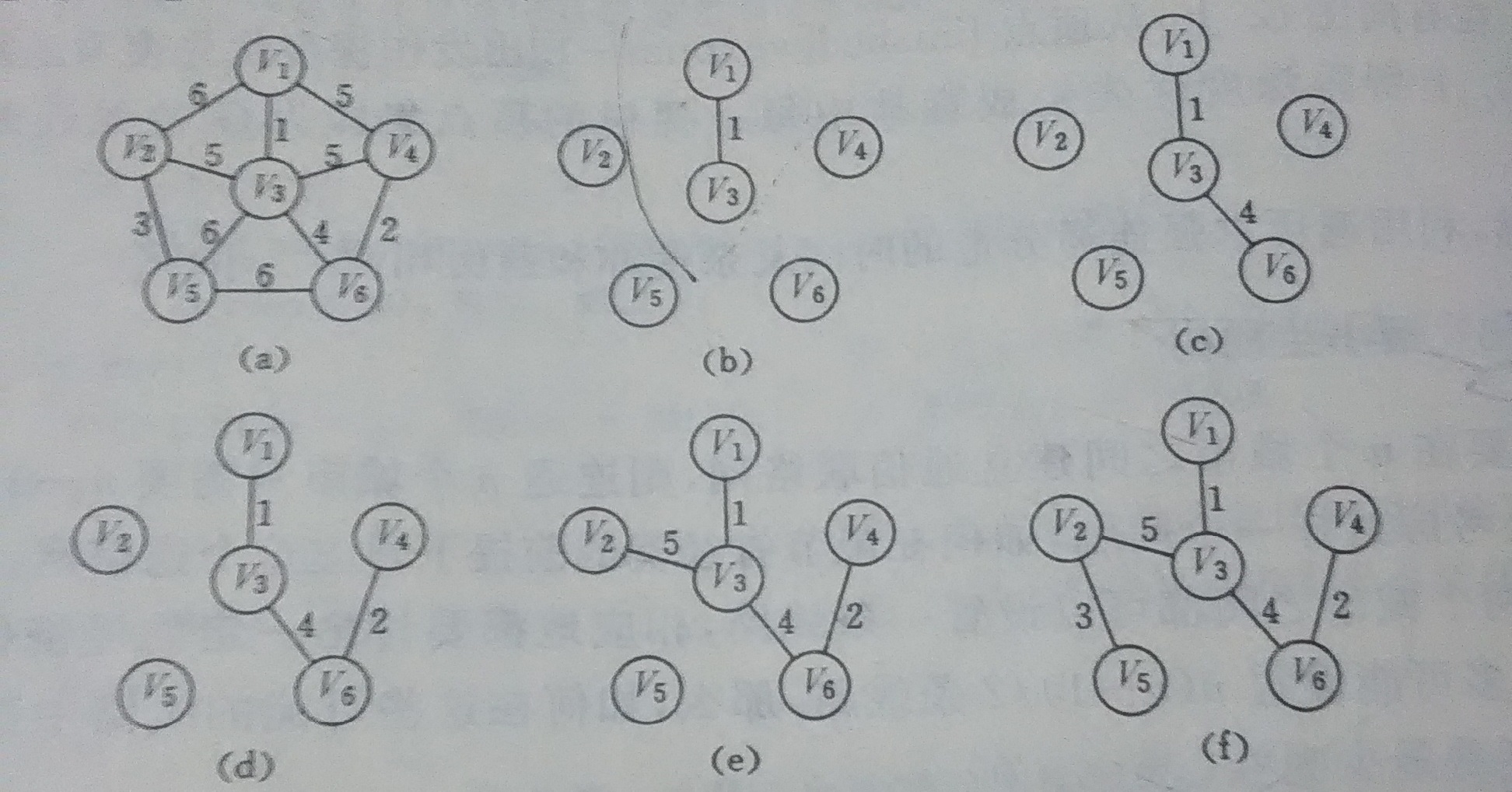
· 普里姆算法:寻找起始顶点邻接的最短边,并入集合,再寻找邻接的最短边 ,不能有环。
· 克鲁斯卡尔算法,寻找最短边,不能有环。
直接上两种算法的代码:
//普里姆算法
struct {
VertexType adjvex;
VRType lowcost;
}closedge[MAX_VERTEX_NUM];
int minmum(MGraph G){
int min=INFINITY;
int index=-1;
for (int i = 0; i < G.vexnum; ++i) {
//最小值大于 该边的权值 且 该边的权值不为 0
if(min>closedge[i].lowcost&&closedge[i].lowcost!=0){
min=closedge[i].lowcost;
index=i;
}
}
return index;
}
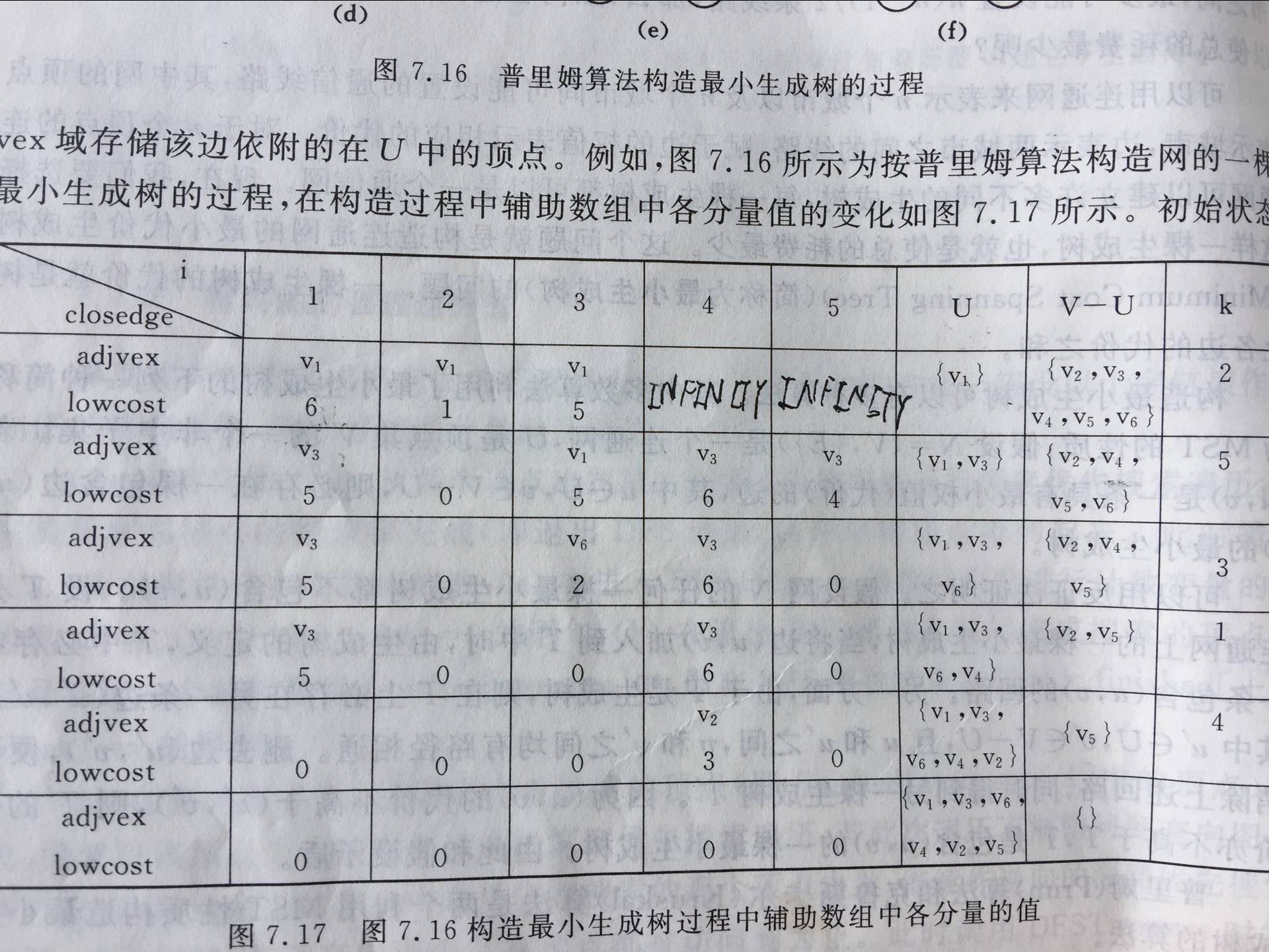
void MiniSpanTree_PRIM(MGraph G,VertexType u){
//书本P174表格
int k=LocateVex(G,u);//该顶点位置 k=0
for (int j = 0; j < G.vexnum; ++j)//辅助数组初始化
if(j!=k)//相当于u顶点 边的信息
closedge[j]={u,G.arcs[k][j].adj};//{adjvex,lowcost}
closedge[k].lowcost=0;//初始,U={u},把u并入集合
for (int i = 1; i < G.vexnum; ++i) {//选择其余G.vexnum-1个顶点
k=minmum(G); //求出T的下一个结点,第k顶点
printf("%d-->%d\n",closedge[k].adjvex,G.vexs[k]);//输出 生成树边
closedge[k].lowcost=0;//第k顶点并入U集
for(int j=0;j<G.vexnum;++j)
if(G.arcs[k][j].adj<closedge[j].lowcost)
//新顶点并入U后重新选择最小边
closedge[j]={G.vexs[k],G.arcs[k][j].adj};
}
}
//克鲁斯卡尔算法,自己写的
typedef struct {
int beginNum; //存放顶点下标
int endNum;
VertexType begin;//顶点名称
VertexType end;
VRType weight;//权重
}Edge[MAX_EDGE_NUM];//边集数组
void MiniSpanTree_Kruskal(MGraph G){
Edge edge[G.arcnum];
int set[G.vexnum];
//初始化辅助数组
for (int i = 0; i < G.vexnum; ++i) {
set[i]=i;//{0,1,2,3,4,5,....}
}
int k=0;
//得到边集数组
for (int i = 0; i < G.vexnum; ++i)
for (int j = 1; j < G.vexnum; ++j)
if (i<j&&G.arcs[i][j].adj!=INFINITY){
edge[k]->beginNum=i;
edge[k]->endNum=j;
edge[k]->begin=G.vexs[i];
edge[k]->end=G.vexs[j];
edge[k]->weight=G.arcs[i][j].adj;
k++;
}
VertexType temp;
VRType adj;
//边集数组,按权重从小到大
for (int i = 0; i < G.arcnum; ++i)
for (int j = i+1; j < G.arcnum; ++j)
if(edge[i]->weight>edge[j]->weight){
temp=edge[i]->begin;
edge[i]->begin=edge[j]->begin;
edge[j]->begin=temp;
temp=edge[i]->end;
edge[i]->end=edge[j]->end;
edge[j]->end=temp;
adj=edge[i]->weight;
edge[i]->weight=edge[j]->weight;
edge[j]->weight=adj;
k=edge[i]->beginNum;
edge[i]->beginNum=edge[j]->beginNum;
edge[j]->beginNum=k;
k=edge[i]->endNum;
edge[i]->endNum=edge[j]->endNum;
edge[j]->endNum=k;
}
int a,b;
for (int i = 0; i < G.arcnum; ++i) {
if(set[edge[i]->beginNum]!=set[edge[i]->endNum]){
//如果辅助数组中,对应数字不同
//输出该边,修改辅助数组中数字
//如果set[edge[i]->beginNum]为a
//set[edge[i]->endNum]为b
//那么把辅助数组中所有为b的改为a
printf("%d->%d weight:%d\n",edge[i]->begin,edge[i]->end,edge[i]->weight);
a=set[edge[i]->beginNum];
b=set[edge[i]->endNum];
for (int j = 0; j < G.vexnum; ++j)
if(set[j]==b)
set[j]=a;
}
}
}
· 普里姆算法的时间复杂度为O(n^2),与网中的边数无关,适用于求边稠密的最小生成树。
· 库鲁斯卡尔的时间复杂度为O(eloge),e为网中边的数目,适合于求边稀疏的最小生成树。
拓扑排序
· 一个无环的有向图称为无环图(Directed Acyclic Graph),简称DAG图。
· 所有的工程或者某种流程都可以分为若干个小的工程或者阶段,
称这些小的工程或阶段为"活动"。
· 在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,
这样的有向图为顶点表示活动的网,称之为AOV网。
· AOV网中的弧表示活动之间存在某种制约关系,且不能存在回路。
· 拓扑序列:设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列V1,V2,...,Vn
满足若从顶点Vi到Vj有一条路径,则在顶点序列中顶点Vi必在顶点Vj之前。则称
这样的顶点序列为拓扑序列。
· 拓扑排序:就是对一个有向图构造拓扑序列的过程。
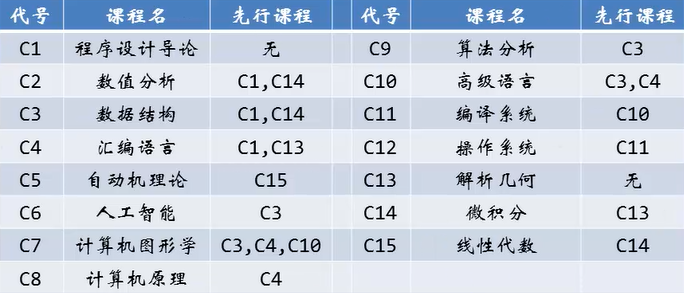
· 拓扑序列(其中一种):
1,13,4,8,15,5,2,3,10,11,12,7,6,9
注:前面的必须指向后面的。
· 对AOV网进行拓扑排序的方法和步骤如下:
-从AOV网中选择一个没有前驱的顶点(入度为0)并输出他。
-从网中删去该顶点,并且删去从该顶点发出的全部有向边。
-重复上述两步,直到剩余网中不再存在没有前驱的顶点为止。
· 由刚才我们那幅AOV网图,我们可以用邻接表(因为需要删除顶点,所以
选择邻接表会更加方便)数据结构表示:
代码实现:
int TopologicalSort(ALGraph G){
//有向图G采用邻接表存储结构
//若G无回路,则输出G的顶点的一个拓扑序列并返回1,否则0
SqStack S;
ArcNode *p;
int i,k;
InitStack(S);
for ( i = 0; i < G.vexnum; ++i) {
if(G.vertices[i]->in==0)
Push(S,i); //入度为0的顶点下标入栈
}
int count=0; //对输出顶点计数
while (!StackEmpty(S)){
Pop(S,i); //输出i号顶点,并计数
printf("%d,%d\n",i,G.vertices[i]->data);
++count;
for(p=G.vertices[i]->firstarc;p;p=p->nextarc){
k=p->adjvex; //对i号顶点的每个邻接点的入度减1
if(!(--G.vertices[k]->in)) //若入度为0,则入栈
Push(S,k);
}
}
if(count<G.vexnum)
return 0;
else
return 1;
}
算法时间复杂度:
-对一个具有n个 顶点,e条边的网来说,初始建立入度为零的顶点栈,
要检查所有顶点一次,执行时间为O(n)。
-排序中,若AOV网无回路,则每个顶点入出栈各一次次,每个表结点
被检查一次,因而执行时间是O(n+e)。
-所以整个算法时间复杂度是O(n+e)。
关键路径
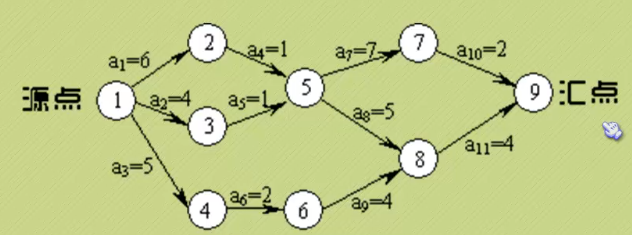
· AOE网:在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,
用边上的权值表示活动的持续时间,这种有向图的边表示活动的网称为AOE网。
· 把AOE网中入度为零的顶点称为始点或源点,出度为零的顶点称为终点或汇点。
· 路径长度最长的路径叫做关键路径。
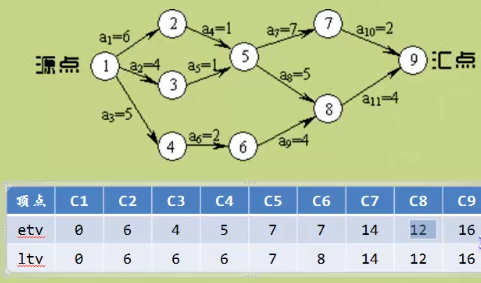
-etv(Earliest Time Of Vertex):事件最早发生时间,就是顶点的最早发生时间。
-ltv(Latest Time Of Vertex):事件最晚发生时间,就是每个顶点对应的事件最晚
需要开始的时间,如果超出此时间将会延误整个工期。
从后面往前看,减去这个工时就为最晚发生时间
例如:C8的etv为12,C6的ltv为12-4=8
-ete(Earliest Time Of Edge):活动的最早开工时间,就是弧的最早发生时间。
-lte(Latest Time Of Edge):活动的最晚发生时间,就是不推迟工期的最晚开工时间。
类似ltv算法,也要倒着过来。
代码实现:
//拓扑排序
int TopologicalSort(ALGraph G) {
//有向图G采用邻接表存储结构
//若G无回路,则输出G的顶点的一个拓扑序列并返回1,否则0
SqStack S;
ArcNode *p;
int i, k;
InitStack(S);
for (i = 0; i < G.vexnum; ++i) {
if (G.vertices[i]->in == 0)
Push(S, i); //入度为0的顶点下标入栈
}
int count = 0; //对输出顶点计数
while (!StackEmpty(S)) {
Pop(S, i); //输出i号顶点,并计数
printf("%d,%d\n", i, G.vertices[i]->data);
++count;
for (p = G.vertices[i]->firstarc; p; p = p->nextarc) {
k = p->adjvex; //对i号顶点的每个邻接点的入度减1
if (!(--G.vertices[k]->in)) //若入度为0,则入栈
Push(S, k);
}
}
if (count < G.vexnum)
return 0;
else
return 1;
}
//关键路径
int ve[];//顶点最早开始时间
int vl[];//顶点最晚开始时间
int TopologicalOrder(ALGraph G, SqStack &T) {
//有向网G采用邻接表存储结构,求各顶点事件的最早发生时间ve(全局变量)
//T为拓扑序列顶点栈,S为零入度顶点栈
//若G无回路,则用栈T返回G的一个拓扑序列,返回1,否则0
SqStack S;
ArcNode *p;
int i, k, j;
InitStack(S);
InitStack(T);
for (i = 0; i < G.vexnum; ++i) {
if (G.vertices[i]->in == 0)
Push(S, i); //入度为0的顶点下标入栈
ve[i] = 0; //初始化
}
int count = 0;
while (!StackEmpty(S)) {
Pop(S, j); //j号顶点入T栈并计数
Push(T, j);
++count;
for (p = G.vertices[j]->firstarc; p; p = p->nextarc) {
k = p->adjvex; //对j号顶点的每个邻接点的入度减1
if (!(--G.vertices[k]->in)) //若入度减为0,则入栈
Push(S, k);
//当前出栈j号顶点的 最早发生时间+ 当前循环连接k号顶点的权值 >k号顶点最早 发生时间
if (ve[j] + *(p->info) > ve[k])
//k号顶点的最早发生时间=出栈顶点号的最早发生时间+与之相连边的权值
ve[k] = ve[j] + *(p->info);
}
}
if (count < G.vexnum) //该有向网有回路
return 0;
else
return 1;
}
int CriticalPath(ALGraph G) {
//G为有向网,输出G的各项关键活动
int j, k, dut, ee, el;
char tag;
SqStack T;
ArcNode *p;
if (!TopologicalOrder(G, T))
return 0;
for (int i = 0; i < G.vexnum; ++i) //初始化顶点事件的最迟发生时间
vl[i] = ve[G.vexnum - 1];
while (!StackEmpty(T)) //按拓扑逆序求各顶点的vl值
//依附于j号顶点的第一条边(包含边权重和指向的顶点)
for (Pop(T, j), p = G.vertices[j]->firstarc; p; p = p->nextarc) {
//该弧指向顶点的位置k
k = p->adjvex;
//该弧权重
dut = *(p->info);
//k的最迟发生时间-该弧权重<初始顶点最迟发生时间
if (vl[k] - dut < vl[j])
vl[j] = vl[k] - dut;
}
for (j = 0; j < G.vexnum; ++j)
for (p = G.vertices[j]->firstarc; p; p = p->nextarc) {
k = p->adjvex;
dut = *(p->info);
//注意ve,vl是顶点的最早和最晚发生时间
//ee,el才是弧的最早和最晚发生时间
//关键路径是对弧而言
ee = ve[j];//该弧最早发生时间=该弧起始顶点最早发生时间
el = vl[k] - dut;//该弧最晚发生时间=该弧结束顶点最晚发生时间-权重
//带* 为关键
tag = (ee == el) ? '*' : '';
printf("起始顶点:%d 结束顶点:%d 该弧权重:%d 最早开始时间:%d 最晚开始时间:%d 是否关键:%c", j, k, dut, ee, el, tag);
}
}
· 这两种算法的时间复杂度均为O(n+e),前一种算法的常数因子要小些。由于计算弧的活动
最早开始时间和最迟开始时间的复杂度为O(e),所以总的求关键路径的时间复杂度O(n+e)
最短路径
· 在网图和非网图中,最短路径的含义是不同的。
-网图是两顶点经过的边上权值之和最少的路径。
-非网图是两顶点之间经过的边数最少的路径。可以看成网图,权值都为1。
· 把路径起始的第一个顶点称为源点,最后一个顶点称为终点。
· 关于最短路径,分为两种算法:
迪杰斯特拉算法
git图演示
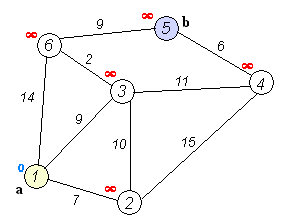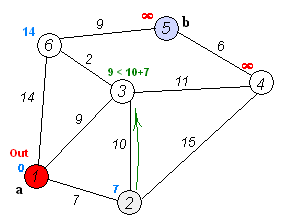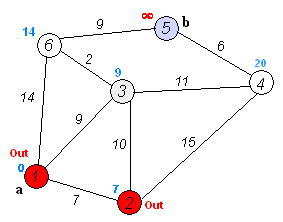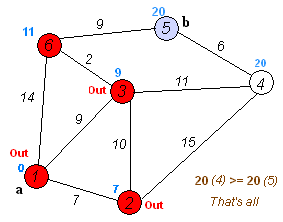
-初始所有顶点路径长为∞,设源点为0。
-搜索该源顶点的路径,依次标上花费路径长度,然后归入S集(表示已遍历)
-逐个搜索除S集合外所有已经标有花费路径长度的顶点,无需遍历归入S集顶点
遍历到其他顶点,若花费小于其标值,则修改之,遍历完成后,并入S集。
-重复上步步骤。
//最短路径,迪杰斯特拉算法
typedef int Patharc[MAX_VERTEX_NUM];//用于存储最短路径下标的数组
typedef int ShortPathTable[MAX_VERTEX_NUM];//用于存储到各点最短路径的权值和
void ShortestPath_DIJ(MGraph G, int V0, Patharc &P, ShortPathTable &D) {
int v, w, min, k = NULL;
int final[MAX_VERTEX_NUM]; //final[w]=1 表示已经求得顶点V0到Vw的最短路径
//初始化数据
for (v = 0; v < G.vexnum; v++) {
final[v] = 0; //全部顶点初始化为未找到最短路径
D[v] = G.arcs[V0][v].adj; //将与V0点有连线的顶点加上权值
P[v] = 0; //初始化路径数组P为0
}
D[V0] = 0; //V0至V0路径为0
final[V0] = 1;//V0至V0不需要求路径
//开始主循环,每次求得V0到某个v顶点的最短路径
for (v = 1; v < G.vexnum; v++) {
min = INFINITY;
//循环后得到一个已知最短路径的顶点,作为发散修正的顶点
for (w = 0; w < G.vexnum; w++)
if (!final[w] && D[w] < min) {
k = w;
min = D[w];
}
final[k] = 1; //将目前找到的最近的顶点置1
//修正当前最短路径 及距离
//从该顶点发散出去的各个顶点距离修正
for (w = 0; w < G.vexnum; w++)
//如果经过v顶点的路径比现在这条路径的长度短的话,更新
if (!final[w] && (min + G.arcs[k][w].adj < D[w])) {
D[w] = min + G.arcs[k][w].adj;//修改当前路径长度
P[w] = k; //存放前驱顶点
}
}
}
· 第一个FOR循环的时间复杂度是O(n),第二个FOR循环共进行n-1次,
每次执行时间是O(n),所以总的时间复杂度是O(n^2)。
· 如果用带权的邻接表作为有向图的存储结构,则虽然修改D的时间可以减少,
但由于在D向量中选择最小分量的时间不变,所以总时间仍为O(n^2)。
· 如果只希望找到源点到某一个特定终点的最短路径,这个问题和求
源点到其他所有顶点的最短路径一样复杂,其时间复杂度也是O(n^2)。
佛洛依德算法
· 从任意阶段i到任意节点j的最短路径只有2种可能,一种是直接从i到j另一种是
从i经过若干个节点k到j。所以,假设Dis(i,j)为节点u到节点v的最短路径的距离,
对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,
证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),
这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
· 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
· 对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
十字交叉法
方法:两条线,从左上角开始计算一直到右下角如图所示
给出矩阵,其中矩阵A是邻接矩阵,而矩阵Path记录u,v两点之间最短路径所必须经过的点。
算法实现:
//最短路径,佛洛依德算法
typedef int PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef int DistancMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
void ShortestPath_FLOYD(MGraph G, PathMatrix &P, DistancMatrix &D) {
int v, w, k;
//初始化D和P
for (v = 0; v < G.vexnum; v++)
for (w = 0; w < G.vexnum; w++) {
D[v][w] = G.arcs[v][w].adj;
P[v][w] = -1;
}
//算法核心
for (k = 0; k < G.vexnum; k++)
for (v = 0; v < G.vexnum; v++)
for (w = 0; w < G.vexnum; w++)
if (D[v][w] > D[v][k] + D[k][w]) {
D[v][w] = D[v][k] + D[k][w];
P[v][w] = P[v][k];
}
}· 此算法时间复杂度为O(n^3)。