数据结构(C语言版 严蔚敏著)——树

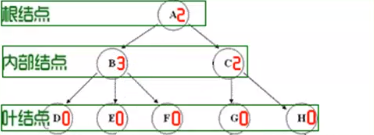
· 树（tree）是n（n>=0）个结点的有限集。当n=0时成为空树，在任意一颗非空树中：

//这里只需掌握定义，重点在二叉树 

    -有且仅有一个特定的称为根（Root）的结点；

    -当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、...、Tm,

     其中集合本身又是一棵树，并且称为根的子树(SubTree)。

    - n>0时，根结点是唯一的，坚决不可能存在多个根结点。

    - m>0时，子树的个数是没有限制的，但它们互相是一定不会相交的。

· 结点拥有的子树称为结点的度（Degree），树的度取树内各结点的度的最大值 。

    -度为0的结点称为叶结点（Leaf）或终端结点。

    -度不为0的结点称为分支结点或非终端结点，除根结点外 ，分支结点也称为内部结点。

· 结点的子树的根称为结点的孩子(Child),相应的，该结点称为孩子的双亲(Parent),

  同一双亲的孩子之间互称为兄弟(Sibling)。

· 结点的祖先是从根到该结点所经分支上的所有结点。

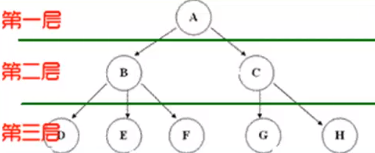
· 结点的层次(Level)从根开始定一起，根为第一层，根的孩子为第二层。

· 其双亲在同一层的结点互为堂兄弟。

· 树中结点的最大层次称为树的深度(Depth)或高度。

· 如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树

  为有序树，否则称为无序树。

二叉树

定义

· 二叉树是n(n>=0)个结点 的 有限集合，该集合或者为空集(空二叉树)，或者由

  一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

特点

· 每个结点 最多 有两棵子树，所以二叉树中不存在度大于2的结点。

· 左子树和右子树是有顺序的,次序不能颠倒。

· 即使树中某节点只有一棵子树，也要区分它是左子树还是右子树。

五种基本形态

· 空二叉树

· 只有一个根结点

· 根结点只有左子树

· 根结点只有右子树

· 根结点既有左子树又有右子树

满二叉树

    -在一棵二叉树中，如果所有分支点都存在左子树和右子树，并且所有叶子都在同一层上，

     这样的二叉树称为满二叉树。

· 满二叉树的特点有：

    -叶子只能出现在最下一层。

    -非叶子结点的度一定是2。

    -在同样深度的二叉树中，满二叉树的结点个数一定最多，同时叶子也是最多。

完全二叉树

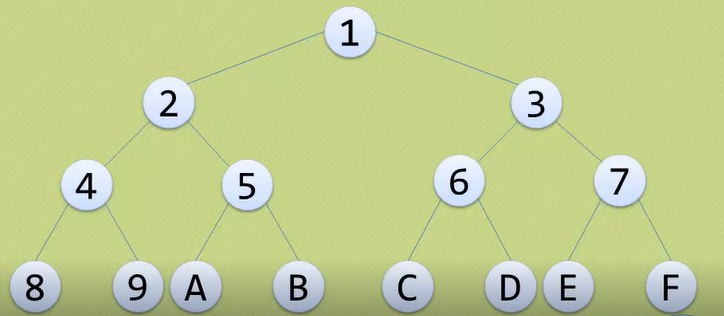
· 对一棵具有n个结点的二叉树按层序编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树

  中编号为i的结点位置完全相同，则这颗 二叉树称为完全二叉树。

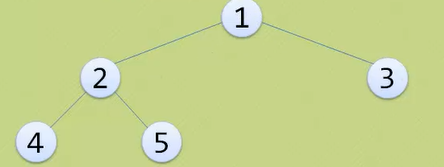
· 完全二叉树的特点有：

    -叶子结点只能出现在最下两层。

    -最下层的叶子一定集中在左部连续位置。

    -倒数第二层，若有叶子结点，一定都在右部连续位置。

    -如果结点度为1，则该结点只有左孩子。

    -同样结点数的二叉树，完全二叉树的深度最小。

· 注意：满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树。

二叉树的性质

· 性质一：在二叉树的第i层上至多有2^(i-1)个结点(i>=1)。

· 性质二：深度为k的二叉树至多有2^k-1个结点(k>=1)。

· 性质三：对任何一棵二叉树T，如果其终端结点数为n0,度为2的结点数为n2，则n0=n2+1。

    -推导过程

    -首先再假设度为1的结点数为n1，则二叉树T的结点总数n=n0+n1+n2

    -其次发现连接树总是等于总结点数n-1，并且等于n1+2*n2

    -所以n-1=n1+2*n2

    -所以n0+n1+n2-1=n1+n2+n2

    -最后n0=n2+1

· 性质四：具有n个结点的完全二叉树的深度为取下整的(log2n)+1

    -由满二叉树的定义结合性质二可得，深度为k的满二叉树的结点树n一定是2^k-1。

    -对于满二叉树可以通过n=2^k-1推得满二叉树的深度为k=log2（n+1）

    -对于倒数第二层的满二叉树我们同样很容易回推出它的结点数为n=2^(k-1)-1

    -所以完全二叉树的结点数的取值范围是：2^(k-1)-1<n<=2^k-1

    -由于n是整数，n<=2^k-1可以看成n<2^k

    -同理2^(k-1)-1<n可以看成2^(k-1)<=n

    -所以2^(k-1)<=n<2^k

    -不等式 两边同时取对数，得到k-1<=log2n<k

    -由于k是深度，必须取整，所以k为取下整的(log2n)+1

· 性质五：如果对一棵有n个结点的完全二叉树(其深度为(log2n)+1)的结点

  按层序编号，对任一结点i(1<=i<=n)有以下性质：

    -如果i=1,则结点i是二叉树的根，无双亲；如果i>1，则其双亲结点[i/2]取下整

    -如果2i>n,则结点i无左孩子(结点i为叶子结点)；否则其左孩子结点是2i

    -如果2i+1>n,则结点i无右孩子；否则其右孩子是结点2i+1

二叉链表

存储结构：

typedef char TElemType;
typedef struct BiTNode{
    TElemType data;
    BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;

创建一个二叉树

void CreateBiTree(BiTree &T){
    //按先序遍历输入结点，左孩子或右孩子为空，用空格代替
    char c;
    scanf("%c",&c);
    if(c==' '){
        //如果为空格，则指向的左孩子或者右孩子为空
        T=NULL;
    } else{
        //创建结点，按照先序遍历创建
        T=(BiTree)malloc(sizeof(BiTNode));
        if(!T)
            exit(0);
        T->data=c;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}

二叉树的遍历

· 二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得

  每个结点被访问一次且仅被访问一次。

· 二叉树的遍历次序不同于线性结构，线性结构最多也就是分为顺序、循环、双向等

  简单的遍历方式。

· 树的结点之间不存在唯一的前驱和后继这样的关系，在访问一个结点后，下一个被

 访问的结点面临着不同的选择。

· 二叉树的遍历方式可以很多，主要有下面三种：

· 前序遍历：

    -若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

· 中序遍历：

    -若树为空，则空操作返回，否则从根结点开始(注意并不是先访问根结点)，中序

      遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。

· 后序遍历：

    -若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后根结点。

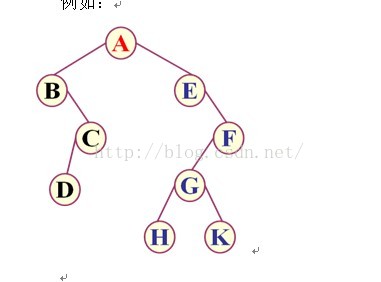
    先序遍历：ABCDEFGHK

    中序遍历：BDCAEHGKF

    后序遍历：DCBHKGFEA

递归遍历算法代码实现：

void  PrintElement(TElemType e){
    printf("%c",e);
}

void PreOrderTraverse(BiTree T){
    if(T){
        //先序遍历
        //三种遍历方式只不过更换下面三句语句的顺序
        PrintElement(T->data);
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}
void InOrderTraverse(BiTree T){
    //中序遍历
    if(T){
        InOrderTraverse(T->lchild);
        PrintElement(T->data);
        InOrderTraverse(T->rchild);
    }
}

void PostOrderTraverse(BiTree T){
    //后序遍历
    if(T){
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
        PrintElement(T->data);
    }
}

非递归的两种算法：

· 另需定义一个栈，存储结点

#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10   //存储空间分配增量
typedef struct {
    BiTree *base;    //在栈构造之前和销毁之后，base值为NULL
    BiTree *top;     //栈顶指针
    int stacksize;      //当前已分配的存储空间，以元素为单位
} SqStack;
int InitStack(SqStack &S) {
    //构造一个空栈S
    S.base = (BiTree *) malloc(STACK_INIT_SIZE * sizeof(BiTree));
    //存储分配失败
    if (!S.base)
        exit(0);
    S.top = S.base;
    S.stacksize = STACK_INIT_SIZE;
    return 1;
}


int Push(SqStack &S, BiTree e) {
    //插入元素e为新的栈顶元素
    if (S.top - S.base >= S.stacksize) {
        //栈满，追加存储空间
        S.base = (BiTree *) realloc(S.base,
                                       (S.stacksize + STACKINCREMENT) * sizeof(BiTree));
        //出错退出
        if (!S.base)
            exit(0);
        //使top指针重新回到栈顶
        S.top = S.base + S.stacksize;
        S.stacksize += STACKINCREMENT;
    }
    *S.top++ = e;//赋值后，指针上移
    return 1;
}

int Pop(SqStack &S, BiTree &e) {
    //若栈不为空，则删除S的栈顶元素，用e返回其值
    //并返回1，否则返回0
    if (S.top == S.base)
        return 0;
    //top指针下移，并赋值给e
    e = *--S.top;
    return 1;
}

int GetTop(SqStack S, BiTree &e) {
    //若栈不空，则用e返回S的栈顶元素，并返回1，否则返回0
    if (S.top == S.base)
        return 0;
    e = *(S.top - 1);
    return 1;
}

int StackEmpty(SqStack S) {
    //判断栈是否为空，空则返回1，否则返回0
    if (S.base == S.top)
        return 1;
    else
        return 0;
}
void unInOrderTraverse1(BiTree T){
    //采用二叉链表存储结构
    //中序遍历二叉树T的非递归 算法
    //方法1
    SqStack S;
    BiTree p;
    InitStack(S);//创建栈
    Push(S,T);//头结点入栈
    while (!StackEmpty(S)){//当栈非空时
        while (GetTop(S,p)&&p)//把栈顶元素给p，且p存在
            Push(S,p->lchild);//一直往左，直到尽头
        Pop(S,p);//空指针出栈
        if(!StackEmpty(S)){//判断是否空栈
            Pop(S,p);//最左边的一个结点出栈
            if(!p->data)//访问结点
                exit(0);
            else
                PrintElement(p->data);
            Push(S,p->rchild);//该结点的右子树进栈
        }
    }
}

void unInOrderTraverse2(BiTree T){
    //采用二叉链表存储结构
    //中序遍历二叉树T的非递归 算法
    //方法2
    SqStack S;
    BiTree p;
    //创建栈
    InitStack(S);
    p=T;
    while (p||!StackEmpty(S)){
        if(p){
            //根指针进栈，遍历左子树
            Push(S,p);
            p=p->lchild;
        } else{
            //根指针退栈，访问根结点 ，遍历右子树
            Pop(S,p);
            if(!p->data)
                exit(0);
            else
                PrintElement(p->data);
            p=p->rchild;
        }
    }
}

线索二叉树

普通二叉树在叶子结点中存在空指针，造成了空间浪费，线索二叉树把这些利用起来

并且能提高遍历的效率。就像链表一样，直接指示下一个结点的位置。

需要增加两个标识域

· LTage 为0  lchild域指示结点的左孩子

· LTage 为1  lchild域指示结点的前驱

· RTage 为0  rchild域指示结点的右孩子

· RTage 为1  rchild域指示结点的后继

结构体代码：

typedef char TElemType;
//Link为0表示左右孩子的指针
//Thread为1表示前驱后继的线索
enum PointerTag {
    Link, Thread
};
typedef struct BiThrNode {
    TElemType data;
    struct BiThrNode *lchild, *rchild;
    PointerTag LTag, RTag;
} BiThrNode, *BiThrTree;

中序遍历线索化以及中序遍历二叉线索树T的非递归算法

//全局变量，始终指向刚刚访问过的结点
BiThrTree pre;

void CreateBiThrTree(BiThrTree &T) {
    //遵循前序遍历约定输入
    char c;
    scanf("%c", &c);
    if (c == ' ')
        T = NULL;
    else {
        T = (BiThrTree) malloc(sizeof(BiThrNode));
        if (!T)
            exit(0);
        T->data = c;
        printf("%c", c);
        //先默认它有左右子树
        T->LTag = Link;
        T->RTag = Link;

        CreateBiThrTree(T->lchild);
        CreateBiThrTree(T->rchild);
    }
}

//中序遍历线索化
void InTreading(BiThrTree p) {
    if (p) {
        //递归左孩子线索化
        InTreading(p->lchild);
        //如果该结点没有左孩子，设置LTag为Thread，
        // 并把lchild指向刚刚访问的结点,设为前驱
        if (!p->lchild) {
            p->LTag = Thread;
            p->lchild = pre;
        }
        //如果该结点没有右孩子，设置RTag为Thread，
        // 并把刚刚访问过结点的rchild指向当前结点,设为后继
        if (!pre->rchild) {
            pre->RTag = Thread;
            pre->rchild = p;
        }
        pre = p;
        InTreading(p->rchild);
    }
}

void InOrderThreading(BiThrTree &Thrt, BiThrTree T) {
    //中序遍历二叉树T，并将其中序线索化，Thrt指向头结点
    if (!(Thrt = (BiThrTree) malloc(sizeof(BiThrNode))))
        exit(0);
    //建立头结点
    Thrt->LTag = Link;
    Thrt->RTag = Thread;
    Thrt->rchild = Thrt;//右指针回指
    //若二叉树空，则左指针回指
    if (!T)
        Thrt->lchild = Thrt;
    else {
        Thrt->lchild = T;
        pre = Thrt;
        InTreading(T);//中序遍历进行中序线索化
        //最后一个结点线索化
        pre->rchild = Thrt;
        pre->RTag = Thread;
        Thrt->rchild = pre;
    }
}

void PrintElement(TElemType e) {
    printf("%c", e);
}

void InOrderTraverse_Thr(BiThrTree T) {
    //T指向头结点，头结点的左链lchild指向根结点
    //中序遍历二叉线索树T的非递归算法
    BiThrTree p;
    p = T->lchild;//p指向根结点
    while (p != T) {//空树或遍历结束时,p==T
        while (p->LTag == Link)
            p = p->lchild;
        if (!p->data)
            exit(0);
        else
            PrintElement(p->data);//访问其左子树为空的结点
        while (p->RTag == Thread && p->rchild != T) {
            p = p->rchild;
            PrintElement(p->data);//访问后继结点
        }
        p = p->rchild;
    }
}

树、森林及二叉树的相互转换

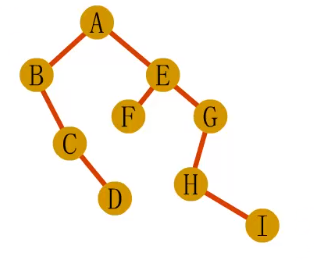
· 树转换成二叉树：

    -加线，在所有兄弟结点之间加一条线。

    -去线，对树中每个结点，只保留它与第一孩子结点的连线，

      删除它与其他孩子结点之间的连线。

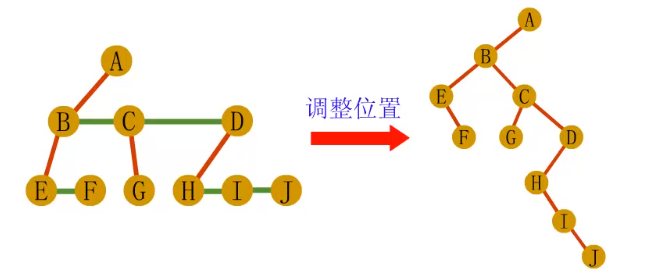
    -层次调整，以树的根结点为轴心，将整棵树顺时针旋转

      一定角度，使之结构层次分明。

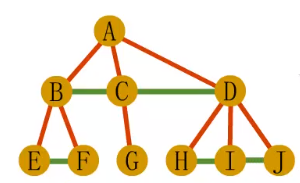
1.第一步，在树中所有兄弟结点之间加一连线

2.第二步，对每个结点，除了保留与其长子的连线外，去掉该结点与其它孩子的连线。

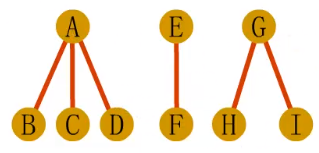
· 森林转换二叉树：

    -先将森林中的每棵树变为二叉树。

    -再将各二叉树的根结点视为兄弟从左至右连在一起，就这样形成一个二叉树。

      把第一棵根结点为根结点，其他根结点连起来，作为它的右子树。

1.第一步，先将森林中的每棵树变为二叉树。

2.第二步，将各二叉树的根结点视为兄弟从左至右连在一起。

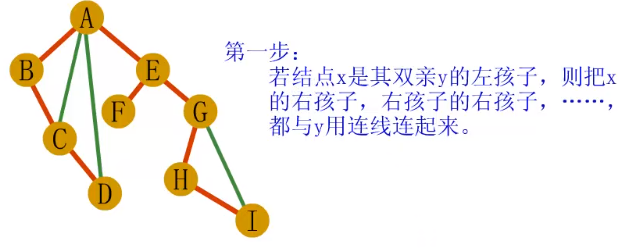
· 二叉树到树、森林的转换

    -二叉树转换为普通树是刚才的逆过程，步骤也就是反过来而已

    -判断一棵二叉树能够转换成一棵树还是森林，那就是只要看这棵

     二叉树的根结点有没有右子树，有的话就是森林，没有就是一棵树。

树与森林的遍历：（理解）

· 树的遍历分为两种方式：一种是先根遍历，另一种是后根遍历。

· 先根遍历：先访问树的根结点，然后再依次先根遍历根的每棵子树。

· 后根遍历：依次遍历每棵子树，然后再访问根结点。

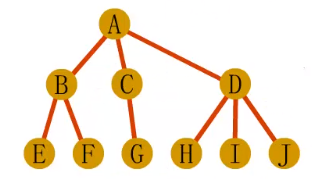
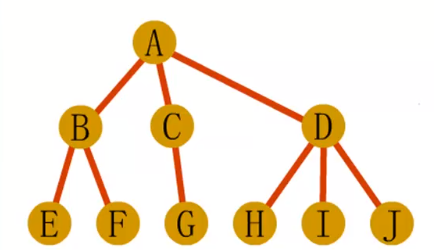
· 先根遍历结果：ABEFCGDHIJ

· 后根遍历结果：EFBGCHIJDA

·森林的遍历也分为前序遍历和后序遍历，其实就是按照树的先根遍历和

 后根遍历依次访问森林的每棵树。

· 有个 惊人的发现：树、森林前根(序)遍历和二叉树的前序遍历结果相同，

  树、森林的后根(序)遍历和二叉树的中序遍历结果相同

· 于是我们可以找到对树和森林遍历这种复杂问题的简单解决方案。

赫夫曼树

· 结点的路径长度：

    -从根结点到该结点的路径上的连接数。

· 树的路径长度：

    -树中每个叶子结点的路径长度之和。

· 结点带权路径长度：

    -结点的路径长度与结点权值的乘积。

· 树的带权路径长度：

    -WPL是树中所有叶子结点的带权路径长度之和。

WPL值越小，说明构造出来的二叉树性能越优

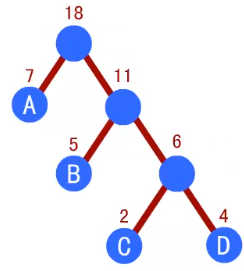
赫夫曼树的构造过程

    -选权值最小的两个结点构成一个二叉树，其双亲结点权值为两个结点权值之和。

    -然后再选取剩下结点的权值最小的，与上一步的二叉树组合，构成新的二叉树，

      如此重复，直到没有结点剩下，这棵二叉树便是赫夫曼树。

构造完成。

注意：为了使得到的哈夫曼树的结构尽量唯一，通常规定生成的哈夫曼树中每个结点的左子树

根结点的权小于等于右子树根结点的权。

赫夫曼编码

· 赫夫曼编码可以有效地压缩数据(通常可以节省20%~90%的空间，具体压缩率依赖于数据的特性)。

· 定长编码、变长编码、前缀码

    -定长编码：类似于ASCII编码。

    -变长编码：单个编码的长度不一致，可以根据整体出现频率来调节。

    -前缀码：没有任何码字是其他码字的前缀。

·  赫夫曼树中没有度为1的结点(这类树又称为严格的二叉树)，则一棵有n个叶子结点的赫夫曼树

   共有2n-1个结点，可以存储在一个大小为2n-1的以为数组中。

· 由于在构成赫夫曼树之后，为求编码需从叶子结点出发走一条从叶子到根的路径；而为编码需

  从根到叶子的路径。则对没个结点而言，既需知双亲的信息，又需知孩子结点的信息。

代码实现：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct {
    int weight;
    int parent, lchild, rchild;
} HTNode, *HuffmanTree;   //动态分配数组存储赫夫曼树
typedef char **HuffmanCode;//动态分配数组存储赫夫曼编码表
//这里可以理解成相当于许多字符串组成的数组

void Select(HuffmanTree htree, int end, int &s1, int &s2) {
    //从数集中选取parent=0,weight最小的两个结点，其下标存入s1,s2
    int min1, min2;
    int i = 1;
    //找到第一个没有双亲的结点
    while (htree[i].parent != 0 && i <= end)
        i++;
    //作为一个参考的最小值，存入min1和s1
    min1 = htree[i].weight;
    s1 = i;
    //下个结点开始
    i++;
    //找到第二个没有双亲的结点，与前面那个作对比
    //较小的放min1和s1，较大的放min2和s2
    while (htree[i].parent != 0 && i <= end)
        i++;
    if (htree[i].weight < min1) {
        min2 = min1;
        s2 = s1;
        min1 = htree[i].weight;
        s1 = i;
    } else {
        min2 = htree[i].weight;
        s2 = i;
    }
    //遍历剩下无双亲的结点
    for (int j = i + 1; j <= end; j++) {
        if (htree[j].parent != 0)
            continue;
        //如果比min1小，min1,s1的数据移到min2,s2
        //并把当前结点的值赋给min1，结点序号给s1
        if (htree[j].weight < min1) {
            min2 = min1;
            min1 = htree[j].weight;
            s2 = s1;
            s1 = j;
        } else if (htree[j].weight >= min1 && htree[j].weight < min2) {
            //如果比min1大且比min2小，
            //则把当前结点值赋给min2，序号给s2
            min2 = htree[j].weight;
            s2 = j;
        }
    }
}

void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n) {
    //w存放n个字符的权值(均>0)，构造赫夫曼树HT，并求出n个字符的赫夫曼树编码HC
    HuffmanTree p;
    int i, s1, s2, start, c, f;
    if (n <= 1)
        return;
    int m = 2 * n - 1;
    HT = (HuffmanTree) malloc((m + 1) * sizeof(HTNode));//0号单元不用
    //注意，第一个结点为空
    //每个结点赋初值
    //n个叶子结点
    for (p = HT+1, i = 1; i <= n; ++i, ++p, ++w)
        *p = {*w, 0, 0, 0};
    //m-n个终端结点
    for (i; i <= m; ++i, ++p)
        *p = {0, 0, 0, 0};
    for (i = n + 1; i <= m; ++i) {
        //在HT[1...i-1]选择parent为0且weight最小的两个结点，其序号分别为 s1和s2
        //组合好后又成为一个新的可选结点，故[1...i-1]
        Select(HT, i - 1, s1, s2);
        //最小两个结点的双亲序号为当前i
        HT[s1].parent = i;
        HT[s2].parent = i;
        //当前i结点左右孩子序号分别是s1，s2
        HT[i].lchild = s1;
        HT[i].rchild = s2;
        //权重为两孩子之和
        HT[i].weight = HT[s1].weight + HT[s2].weight;
    }
    //---从叶子到根逆向求没个字符的赫夫曼编码---
    //分配n+1个字符编码的头指针向量
    //0号位不存放数据
    HC = (HuffmanCode) malloc((n + 1) * sizeof(char *));
    //分配求编码的工作空间
    char *cd = (char *) malloc(n * sizeof(char));
    //最后一个字符为结束符
    cd[n - 1] = '\0';
    //逐个字符求赫夫曼编码
    for (i = 1; i <= n; ++i) {
        start = n - 1;//编码结束符位置
        for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent){
            //从叶子到根逆向求编码
            if (HT[f].lchild == c)
                cd[--start] = '0';
            else
                cd[--start] = '1';
        }
        //为第i个字符分配空间
        HC[i] = (char *) malloc((n - start) * sizeof(char));
        //将遍历得到的编码串复制到HC[i]
        strcpy(HC[i], &cd[start]);
    }
    free(cd);
}

void print_huffman_tree(HuffmanTree htree, int n) {
    printf("Huffman tree:\n");
    int m = 2 * n - 1;
    for (int i = 1; i < m; ++i) {
        printf("node_%d, weight = %d, parent = %d, left = %d, right = %d\n",
               i, htree[i].weight, htree[i].parent, htree[i].lchild, htree[i].rchild);
    }
}

void print_all_huffman_code(HuffmanCode HC, int n) {
    printf("Huffman code:\n");
    for (int i = 1; i <= n; ++i) {
        printf("%d code = %s\n", i, HC[i]);
    }
}

int main() {
    int w[5] = {2, 8, 7, 6, 5};
    int n = 5;
    HuffmanTree HT;
    HuffmanCode HC;
    HuffmanCoding(HT, HC, w, n);

    print_huffman_tree(HT, n);
    print_all_huffman_code(HC, n);
    return 0;
}