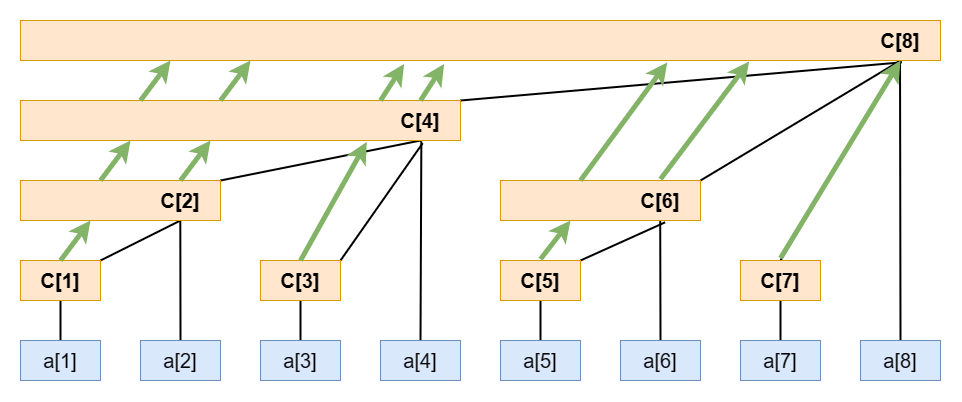
O(N) 建树#
对于树状数组最基本的建树方式,就是每个点加值。
时间复杂度:O(NlogN)
代码实现
int tr[N]; // tr[] 存储树状数组数据
int a[N]; // a[] 存储原数组数据
int n; // 数列长度
int lowbit(int x) { return x & -x; }
void add(int x, c) {
for (int i = x; i <= n; x += lowbit(x))
tr[i] += c;
}
// 建树
void build() {
for (int i = 1; i <= n; i++)
add(i, a[i]);
}
对于 O(N) 建树的应用场景并不是很多,因为普通建树的时间复杂度为 NlogN 。这个时间复杂度对于大部分题目都是可以接受的,除非有些题目故意卡常什么的。
方法一#
我们知道对于树状数组 tr[x] ,它所维护的区间范围是 [x−lowbit(x)+1,x],所以 tr[x]=a[x−lowbit(x)+1,x] 。那么我们就先可以求 a[] 的前缀和,然后通过前缀和 O(1) 求出 [x−lowbit(x)+1,x] 的区间和,从而实现 O(N) 建立树状数组。
代码实现
int tr[N]; // 树状数组数据
int a[N]; // 原数组数据
int sum[N]; // sum[] 存储 a[] 的前缀和
int n; // 数列长度
int lowbit(int x) { return x & -x; }
// 建树
void build() {
// 求 a[] 的前缀和 sum[]
for (int i = 1; i <= n; i++)
sum[i] = sum[i - 1] + a[i];
// 利用前缀和求出区间和,O(N)建树
for (int i = 1; i <= n; i++)
tr[i] = sum[i] - sum[i - lowbit(i)];
}
方法二#
观察上图我们发现,对于 O(logN) 建树的情况,当 C[x] 被更新的时候,它们都会再更新它们的父节点。那么这样就会导致 C[x] 多次更新它的父节点,产生很多重复的计算。
我们还知道,对于 C[x] 的父节点是 C[x+lowbit(x)] 。那么我们就可以从 1 到 n ,让每个 C[i] 节点只更新一次自己的父节点就行了。
用这种方式,同样也可以实现 O(N) 建立树状数组。而且这种方式相对于方法一,会更省事点,也不用提前预处理出来前缀和。
代码实现
int tr[N]; // 树状数组数据
int a[N]; // 原数组数据
int n; // 数列长度
int lowbit(int x) { return x & -x; }
// 建树
void build() {
for (int i = 1; i <= n; i++) {
tr[i] += a[i];
int fa = i + lowbit(i); // 获得父节点下标
if (fa <= n) // 判断父节点是否超出数列范围
tr[fa] += tr[i];
}
}
维护区间和#
单点修改,区间查询#
给定一个长度为 n 的数列,要对数列进行 Q 次以下两种操作:
1 x y:将 x 位置的数加上 y (或者减去 y 、变成 y、乘以 y )。2 x y:查询区间 [x,y] 的和。
这是树状数组最基本的用法。
时间复杂度
- 单点修改 O(logN)
- 区间查询 O(logN)
代码实现
int tr[N];
int a[N];
int n;
int lowbit(int x) { return x & -x; }
// 给 x 位置的数加上 c
void add(int x, int c) {
for (int i = x; i <= n; i += lowbit(i))
tr[i] += c;
}
// 查询 1 ~ x 的区间和
void query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tr[i];
return res;
}
// 使用
add(x, c); // 给 x 位置的数加上 c
add(x, y - (query(x) - query(x - 1))); // 讲 x 位置的数改为 y
int val1 = query(x); // 查询 [1, x] 的区间和
int val2 = query(r) - query(l - 1); // 查询 [l, r] 的区间和
int val3 = query(x) - query(x - 1); // 查询 x 位置的值
区间修改,单点查询#
给定一个长度为 n 的数列,要对数列进行 Q 次以下两种操作:
1 x y k:将区间 [x,y] 里的数都加上 k (或者都减去 k)。2 x:查询 x 位置的值
这里我们需要用到差分,从而利用树状数组来维护差分数组。
- 区间修改:
add(l, k), add(r + 1, -k); - 单点查询:
query(y) - query(x - 1);
时间复杂度
- 区间修改:O(logN)
- 单点查询:O(logN)
代码实现
int tr[N];
int a[N];
int n;
int lowbit(int x) { return x & -x; }
// 给 x 位置的数加上 c
void add(int x, int c) {
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
// 查询 1 ~ x 的区间和
void query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
// 使用
add(r, c), add(l - 1, c); // 讲区间 [l, r] 都加上 c
int val = query(x) + a[x]; // 查询 x 位置的值
区间修改,区间查询#
给定一个长度为 n 的数列,要对数列进行 Q 次以下两种操作:
1 x y k:将区间 [x,y] 里的数都加上 k (或者都减去 k)。2 x y:查询 [x,y] 的区间和。
平时遇到这种问题,我们一般都会选择用线段树来解决,但是树状数组也能实现。
这里我们首先想到要用差分数组来实现,但是怎么才能查询区间和呢?
对于数列 a[i] ,它的差分数组为 b[i]=a[i]−a[i−1] ,a[i] 的值就是 b[i] 的前缀和。那么对于 a[i] 的前缀和就有,
那么就有,那么就有,(1)∑i=1xai=a1+a2+a3+...+ax(2)=b1(3)+b1+b2(4)+b1+b2+b3(5)+b1+b2+b3+b4(6)⋮(7)+b1+b2+b3+b4+⋯+bx(8)那么就有,∑i=1xai=∑i=1x∑j=1ibj
如果我们对所列出的式子进行补充,变成一个矩阵,如下图所示。
如果我们根据列进行求和,那么前缀和的表示公式就能变形为,
(9)∑i=1xai=(b1+b2+b3+...+bx)×(x+1)−(b1+2b2+3b3+...+xbx)(10)=∑i=1xbi−∑i=1xi×bi
这样我们就能把问题转化成维护 bi 和 i×bi 的前缀和数组,从而用两个树状数组来 tr1 和 tr2 来分别维护 bi 和 i×bi 的前缀和。
- 区间查询:获取前缀和,直接根据公式计算。
- 时间复杂度:O(logN)
- 区间修改:分别对 tr1 和 tr2 所维护的前缀和做出相应的修改。
- 时间复杂度:O(logN)
- 对于 tr1 ,执行
add(x, k), add(y + 1, -k); - 对于 tr2 ,执行
add(x, x * k), add(y + 1, (y + 1) * k);
代码实现
#define int long long
int tr1[N]; // 维护 b[i] 的前缀和
int tr2[N]; // 维护 i * b[i] 的前缀和
int a[N]; // 原数组
int n;
int lowbit(int x) { return x & -x; }
// 对树状数组 tr[] 执行加和操作
void add(int tr[], int x, int c) {
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
// 对树状数组 tr[] 执行查询前缀和的操作
int query(int tr[], int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
// 建树
void build() {
for (int i = 1; i <= n; i++) {
int b = a[i] - a[i - 1]; // 差分 b[i]
add(tr1, i, b);
add(tr2, i, i * b);
}
}
// 查询数列的前缀和
int pre_sum(int x) {
return query(tr1, x) * (x + 1) - query(tr2, x);
}
// 执行操作
// 建树(初始化)
build();
// 区间查询
int val = pre_sum(y) - pre_sum(x - 1); // [x, y] 的区间和
// 区间修改
add(tr1, x, k), add(tr1, y + 1, -k); // 修改 tr1[]
add(tr2, x, x * k), add(tr2, y + 1, (y + 1) * -k); // 修改 tr2[]
整合的维护区间和的完成代码,支持区间修改和区间查询(函数封装好)
维护二维子矩阵和(二维树状数组)#
单点修改,子矩阵查询#
给定一个 n×m 的矩阵 A,要对矩阵进行 Q 次以下两种操作:
1 x y k:将元素 Ax,y 加上 k (或者都减去 k)。2 a b c d:查询左上角为 (a,b) ,右上角为 (c,d) 的子矩阵内所有数的和。
二维树状数组就是树状数组套树状数组。就是在原先一维树状数组的基础上,用此树状数组的节点再来建立树状数组,从而实现维护矩阵和的功能。
我们思考树状数组的修改逻辑,就是当某一个节点被修改时,有多少的节点会被影响到,然后再修改这些被影响的节点。所以对于矩阵 A 中节点的改变,就会影响到一维树状数组的节点值,然后做出相对应的修改。同样的,一维树状数组的改变,也会影响到第二维树状数组的节点值,也要做出相对应的修改。
一维树状数组的修改是 O(logN) ,所以会影响到 logN 个节点。对于一维树状数组每个被修改的节点,都需要再 O(logN) 更新二维树状数组的节点值。
所以修改操作的时间复杂度为 O(log2N) 。
而对于二维前缀和的初始化,有 sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j]; (不做具体解释,不会的可以先学一学,下面的也一样)。
同理,对于查询操作,我们知道通过二维前缀和来求子矩阵的式子为,Sum = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];。
那么只需要获取它们维护的前缀和,然后根据公式计算出结果,时间复杂度也为 O(log2N) 。
那么这就是二维树状数组的基本逻辑,从而实现维护矩阵和的功能。
时间复杂度
-
初始化:N2log2N
-
单点修改:O(log2N)
-
子矩阵查询:O(log2N)
代码实现
#define int long long
int tr[N][N]; // 二维树状数组
int a[N][N]; // 原数组
int n, m; // 行高和列宽
int lowbit(int x) { return x & -x; }
// 给 (x, y) 位置的数加上 c
void add(int x, int y, int c) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += c;
}
// 查询 (x, y) 位置的二维前缀和
int query(int x, int y) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
res += tr[i][j];
return res;
}
// 建立二维树状数组(初始化)
void build() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int val = query(i - 1, j)
+ query(i, j - 1)
- query(i - 1, j - 1)
+ a[i][j];
add(i, j, val);
}
}
}
// // 查询左上角为(x1, y1), 右下角为(x2, y2) 的子矩阵的和
int query(int x1, int y1, int x2, int y2) {
return query(x2, y2)
- query(x1 - 1, y2)
- query(x2, y1 - 1)
+ query(x1 - 1, y1 - 1);
}
// 使用
build(); // 初始化
add(x, y, c); // 给 (x, y) 位置的数加上 c
add(x, y, -c); // 给 (x, y) 位置的数减去 c
int sum1 = query(x, y); // 查询左上角为(1, 1), 右下角为(x, y) 的子矩阵的和
int sum2 = query(a, b, c, d); // 查询左上角为(a, b), 右下角为(c, d) 的子矩阵的和
子矩阵修改,单点查询#
给定一个 n×m 的矩阵 A,要对矩阵进行 Q 次以下两种操作:
1 a b c d k:将左上角为 (a,b) ,右上角为 (c,d) 的子矩阵里的每个元素都加上 k (或者都减去 k)。2 x y:询问元素 Ax,y 的值。
和上面进行区间修改,单点查询的相同,这个是用一维树状数组来维护一维差分数组。那么同理,我们也可以用二维树状数组来维护二维差分数组。
对于二维差分数组,我们每次的矩阵修改操作为,b[x1][y1] += c, b[x2 + 1, y1] -= c, b[x1, y2 + 1] -= c, b[x2 + 1][y2 + 1] += c; ,每次的单点查询操作就是求一次二维前缀和。
时间复杂度
- 子矩阵修改:O(log2N)
- 单点查询:O(log2N)
代码实现
#define int long long
int tr[N][N]; // 二维树状数组
int a[N][N]; // 原数组
int n, m; // 行高和列宽
int lowbit(int x) { return x & -x; }
void add(int x, int y, int c) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += c;
}
void query(int x, int y) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
res += tr[i][j];
return res;
}
// 将左上角为 (x1, y1), 右下角为 (x2, y2) 的子矩阵的每个元素都加上 c
void add(int x1, int y1, int x2, int y2, int c) {
add(x1, y1, c);
add(x2 + 1, y1, -c);
add(x1, y2 + 1, -c);
add(x2 + 1, y2 + 1, c);
}
// 使用
add(x1, y1, x2, y2, c); // 将左上角为 (x1, y1), 右下角为 (x2, y2) 的子矩阵的每个元素都加上 c
int val = query(x, y) + a[x][y]; // 查询 (x, y) 位置的元素值
子矩阵修改,子矩阵查询#
给定一个 n×m 的矩阵 A,要对矩阵进行 Q 次以下两种操作:
1 a b c d k:将左上角为 (a,b) ,右上角为 (c,d) 的子矩阵里的每个元素都加上 k (或者都减去 k)。2 a b c d:查询左上角为 (a,b) ,右上角为 (c,d) 的子矩阵内所有数的和。
我们可以像上面处理一维区间和那样思考,通过维护二维前缀和数组来解决问题。
具体思路和推导过程就不赘述了,要想了解的可以看这篇博客:数据结构学习笔记-二维树状数组 - 知乎
具体想法是用四个二维树状数组来分别维护 di,j,(i−1)di,j,(j−1)di,j,(i−1)(j−1)di,j 的二维前缀和数组。
然后通过推导出来的公式来计算前缀和,
sn,m=nm∑i=1n∑j=1mdi,j−m∑i=1n∑j=1m(i−1)di,j−n∑i=1n∑j=1m(j−1)di,j+∑i=1n∑j=1m(i−1)(j−1)di,j
代码实现
#define int long long
int a[N][N], b[N][N], c[N][N], d[N][N]; // 二维树状数组
int n, m;
int lowbit(int x) { return x & -x; }
void add(int x, int y, int v) {
for (int i = x; i <= n; i += lowbit(i)) {
for (int j = y; j <= m; j += lowbit(j)) {
a[i][j] += v;
b[i][j] += (x - 1) * v;
c[i][j] += (y - 1) * v;
d[i][j] += (x - 1) * (y - 1) * v;
}
}
}
int query(int x, int y) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) {
for (int j = y; j; j -= lowbit(j)) {
res += x * y * a[i][j]
- y * b[i][j]
- x * c[i][j]
+ d[i][j];
}
}
return res;
}
// 将左上角为 (x1, y1), 右上角 (x2, y2) 的子矩阵的所有元素加上 c
void add(int x1, int y1, int x2, int y2, int c) {
add(x1, y1, v);
add(x1, y2 + 1, -v);
add(x2 + 1, y1, -v);
add(x2 + 1, y2 + 1, v);
}
// 查询左上角为 (x1, y1), 右上角 (x2, y2) 的子矩阵的元素和
int query(int x1, int y1, int x2, int y) {
return query(x2, y2)
- query(x1 - 1, y2)
- query(x2, y1 - 1)
- query(x1 - 1, y1 - 1);
}
// 使用
add(x1, y1, x2, y2, c); // 将左上角为 (x1, y1), 右上角 (x2, y2) 的子矩阵的所有元素加上 c
int sum = query(x1, y1, x2, y2);// 查询左上角为 (x1, y1), 右上角 (x2, y2) 的子矩阵的元素和
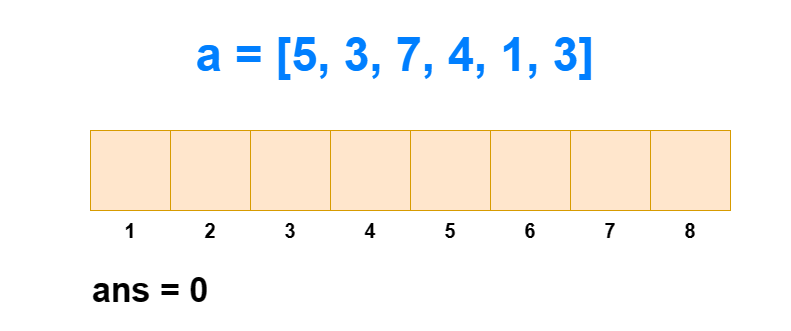
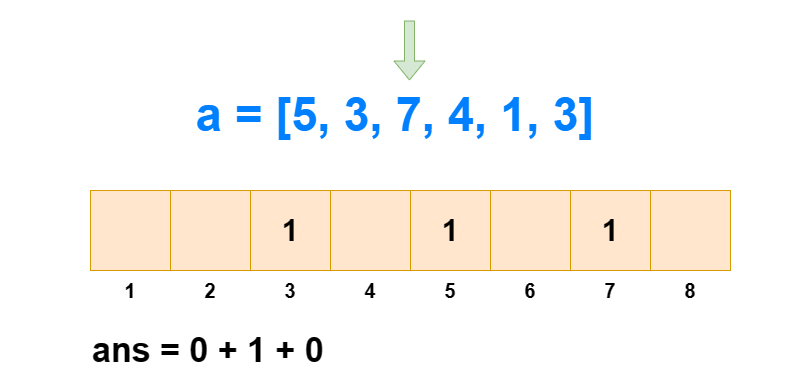
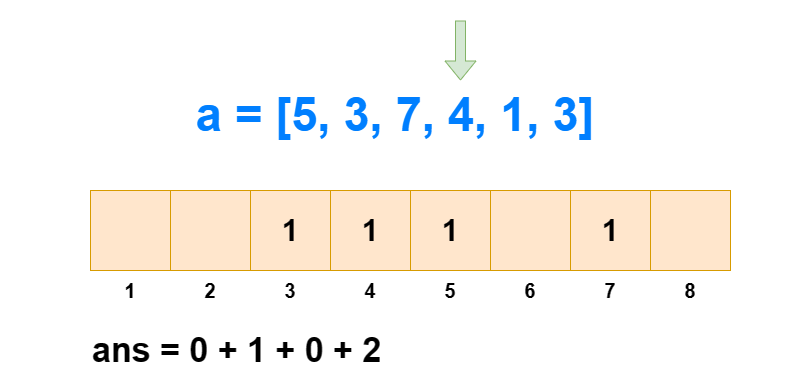
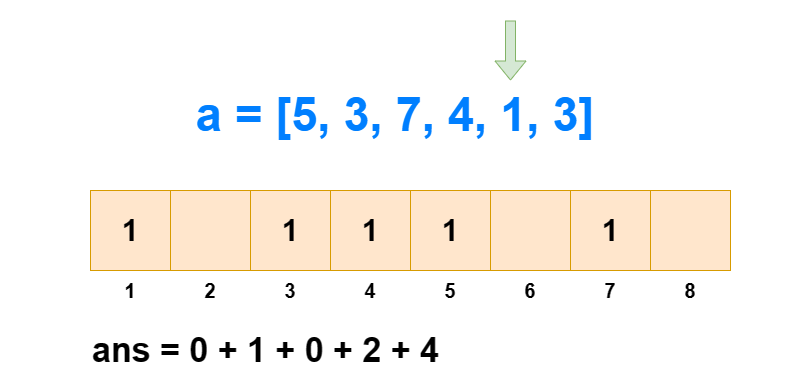
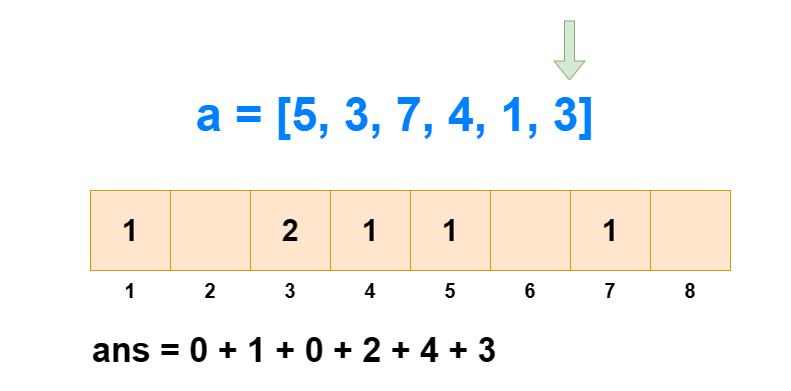
求逆序对个数#
给定一个长度为 n 的数列,求其中逆序对的个数。
逆序对:对于 1≤i<j≤n,有 ai>aj 。
归并排序是可以求一个数列中逆序对的个数的,时间复杂度为 O(logN) 。而树状数组也可以求解此类问题,时间复杂度同样为 O(logN) ,而且空间复杂度相对于归并排序会更低。
对于逆序对个数的求解,树状数组是通过求每个 ai 左边比它大的数的个数,然后全部加和得来的。如果每次遍历查肯定不行,那是怎么求出每个 ai 左边比它大的数的个数的呢?
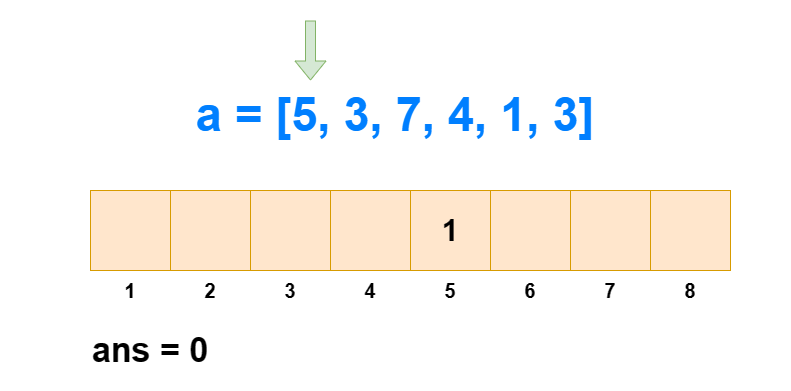
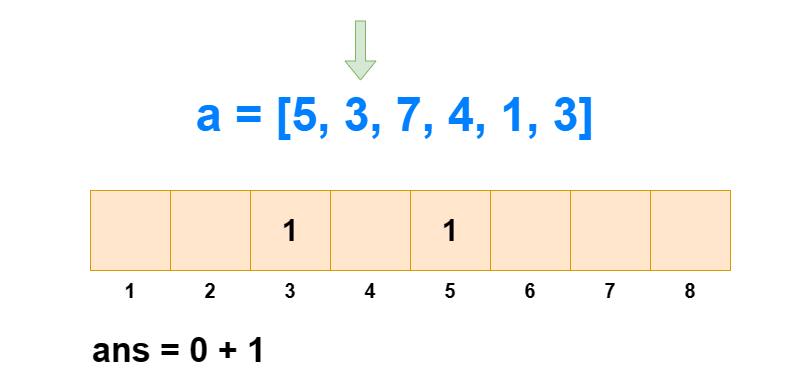
从 1 到 n ,把 ai 作为下标元素,把 ai 位置的数 +1 。然后我们每次查询 1∼ai 的区间和,所得到的值就是 1∼i 中比 ai 小或相等的元素个数(包括 ai 自己)。那么 1∼i 中比 ai 大的元素个数就是 i−sum[1,ai] 。
这样我们遍历 1∼n ,每次 O(logN) 进行前缀和查询和单点修改,那么总的时间复杂度就是 O(NlogN) 。
还有,这样的做法是把 ai 作为下标进行计算。而对于 ai 是负数或者数很大的情况,就需要加上离散化的操作。
如果这样的话,树状数组的时间和空间消耗相对于归并排序都会更多点(虽然总的时空复杂度是相同的)。其实这样就体现出了归并排序求逆序对的好处,它并不用考虑 ai 的取值范围,只能说各有优缺吧。
代码实现
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int tr[N];
int a[N];
int n;
int lowbit(int x) { return x & -x; }
void add(int x, int c) {
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
LL res = 0;
for (int i = 1; i <= n; i++) {
add(a[i], 1);
// 求逆序对的个数
res += i - query(a[i]);
}
cout << res << "\n";
return 0;
}
需要离散化操作的代码
求数列中小于 x 的元素个数#
根据上面求逆序对的思路,我们可以求出数列中小于(大于、小于或等于、大于或等于) x 的元素个数。
同样的,如果数列中有负数或者数很大,就还得需要 O(NlogN) 来进行离散化处理。
这里注意,这种方法只支持离线查询,预处理的时间复杂度为 O(NlogN),对于每次查询的时间复杂度为 O(logN) 。
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int tr[N];
int a[N];
int n;
int lowbit(int x) { return x & -x; }
void add(int x, int c) {
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
// 预处理
for (int i = 1; i <= n; i++)
add(a[i], 1);
// 查询
int x;
cin >> x;
int num1 = query(x - 1); // 查询小于 x 的元素个数
int num2 = query(x); // 查询小于等于 x 的元素个数
int num3 = n - query(x); // 查询大于 x 的元素个数
int num4 = n - query(x - 1);// 查询大于等于 x 的元素个数
return 0;
}