前言
本文是对上一篇文章的补充和总结。
在上一篇文章中,笔者提出了一套基本可用的“动态平衡概率”算法,本文将继续对该算法进行更加深入的探讨,解决上篇文章中的部分遗留问题,以及记录一下对“游戏中的概率”的一些思考:
- 如何计算因增加“保底暴击”而增加的“暴击率”
- 应该使用哪种“动态平衡概率”算法
算法预览
增加“保底暴击”的设定后,总暴击概率的计算方式:
P 保底暴击 = ( 1 − p ) k ⋅ p E 保底暴击 = ∑ k = 10 C ( N A t k − k + 1 ) ⋅ P 保底暴击 ⋅ △ k ( C = C l a m p ( k , 30 , 100 ) ) (此范围为经验值) E 自然暴击 = N A t k ⋅ p E 总暴击 = E 自然暴击 + E 保底暴击 P 总暴击 = p ⋅ E 自然暴击 E 总暴击 其中: p :每次暴击的概率 k 是变量 ,表示第 k 次暴击 △ k = 10 : k 增加的步长(与 k 的初始值相等) ∑ k = 10 C ⋅ ⋅ ⋅ △ k :表示从 k = 10 开始对 ⋅ ⋅ ⋅ 求和, k 自身不断增加,直到 k 达到 ( 30 , 100 ) 的范围, k 的步长为 10 ( N A t k − k + 1 ) :表示试验次数 \begin{align*} P_{保底暴击} &= (1 - p)^{k} · p \\ \\ E_{保底暴击} &= \sum_{k = 10}^{C} (N_{Atk} − k + 1) · P_{保底暴击} · \triangle k \\ (C &= Clamp(k,30,100))(此范围为经验值) \\ \\ E_{自然暴击} &= N_{Atk} · p \\ \\ E_{总暴击} &= E_{自然暴击} + E_{保底暴击} \\ \\ P_{总暴击} &= p · \frac{E_{自然暴击}}{E_{总暴击}} \\ \\ 其中 :& \\ p &:每次暴击的概率 \\ k 是变量 &,表示第 k 次暴击 \\ \triangle k = 10 &: k 增加的步长(与k的初始值相等) \\ \sum_{k = 10}^{C} ··· \triangle k &:表示从k=10开始对···求和,k自身不断增加,直到k达到(30,100)的范围,k的步长为10 \\ (N_{Atk} − k + 1) &:表示试验次数 \\ \end{align*} P保底暴击E保底暴击(CE自然暴击E总暴击P总暴击其中:pk是变量△k=10k=10∑C⋅⋅⋅△k(NAtk−k+1)=(1−p)k⋅p=k=10∑C(NAtk−k+1)⋅P保底暴击⋅△k=Clamp(k,30,100))(此范围为经验值)=NAtk⋅p=E自然暴击+E保底暴击=p⋅E总暴击E自然暴击:每次暴击的概率,表示第k次暴击:k增加的步长(与k的初始值相等):表示从k=10开始对⋅⋅⋅求和,k自身不断增加,直到k达到(30,100)的范围,k的步长为10:表示试验次数
假设 p = 0.2,通过上述公式,发现在攻击100000次后,暴击概率增加的部分是2.4%,这与观察到的基本相符。
计算过程
“保底暴击”发生的概率
为了计算多出来的那部分“暴击率”,我们首先要获得它所有能触发“保底暴击”情况的概率。
第一种情况
我们先讨论连续攻击九次未暴击,第十次自然发生暴击的概率。由于每次攻击都是一个独立事件,可以用几何分布来求出这一概率。
假设暴击率为 p p p,求出攻击 N A t k N_{Atk} NAtk 次中,连续 k − 1 k - 1 k−1 次没有出现暴击的概率:
可以将该问题转化为:连续 k − 1 k - 1 k−1 次未暴击后,第 k k k 次发生暴击的概率(几何分布):
P ( 攻击 k 次才发生暴击 ) = ( 1 − p ) k − 1 ⋅ p p :每次攻击时,发生暴击的概率 k :实验次数 \begin{align*} P(攻击 k 次才发生暴击) &= (1 - p)^{k - 1} · p \\ \\ p &:每次攻击时,发生暴击的概率 \\ k &:实验次数 \\ \end{align*} P(攻击k次才发生暴击)pk=(1−p)k−1⋅p:每次攻击时,发生暴击的概率:实验次数
举个例子,假设暴击率为 0.2,我想求出攻击 N A t k N_{Atk} NAtk次中 ( N A t k > 10 ) (N_{Atk} > 10) (NAtk>10),连续 9 次没有出现暴击的概率,那么就有:
P ( N A t k = 10 ) = ( 1 − 0.2 ) 10 − 1 × 0.2 = 0.0268435456 \begin{align*} P(N_{Atk} = 10) &= (1 - 0.2)^{10 - 1} \times 0.2 = 0.0268435456 \\ \\ \end{align*} P(NAtk=10)=(1−0.2)10−1×0.2=0.0268435456
其他情况
假设我们现在没有设置“保底暴击”,那么在进行很多次试验之后,肯定会出现连续几十次未暴击的情况。
再为其设置“保底暴击”,其实相当于在一系列连续多次未暴击的情况中,将间隔 k − 1 k - 1 k−1 个未暴击之后的第 k k k 个攻击,改为暴击。
所以我们面对的其他情况就有 ( 1 − p ) 2 k − 1 (1 - p)^{2k - 1} (1−p)2k−1、 ( 1 − p ) 3 k − 1 (1 - p)^{3k - 1} (1−p)3k−1 等等。
“保底暴击”的概率
当暴击率为 0.2 时,连续 9 次未暴击后,第 10 次为“保底暴击”。我想求出所有保底暴击情况的概率,那么就有以下公式:
P 保底暴击 = ∑ k = 10 N A t k ( ( 1 − p ) k − 1 ⋅ p ) ⋅ △ k 其中: p = 0.2 ,是每次暴击的概率 △ k = 10 ,是 k 增加的步长 k 是变量 ,表示第 k 次暴击 \begin{align*} P_{保底暴击} &= \sum_{k = 10}^{N_{Atk}} ((1 - p)^{k - 1} · p) · \triangle k \\ \\ 其中 :& \\ p = 0.2 &,是每次暴击的概率\\ \triangle k = 10 &,是 k 增加的步长\\ k 是变量 &,表示第 k 次暴击\\ \end{align*} P保底暴击其中:p=0.2△k=10k是变量=k=10∑NAtk((1−p)k−1⋅p)⋅△k,是每次暴击的概率,是k增加的步长,表示第k次暴击
“保底暴击”的数学期望
在求出所有“保底暴击”情况的概率之后,只需要将概率乘以试验的总次数,就可以得到数学期望了:
E 保底暴击 = ∑ k = 10 N A t k ( N A t k − k + 1 ) ⋅ ( ( 1 − p ) k − 1 ⋅ p ) ⋅ △ k 其中: p :每次暴击的概率 k 是变量 ,表示第 k 次暴击 △ k : k 增加的步长 ( N A t k − k + 1 ) :表示试验总次数 \begin{align*} E_{保底暴击} = \sum_{k = 10}^{N_{Atk}} (N_{Atk} − k &+ 1) · ((1 - p)^{k - 1} · p) · \triangle k \\ \\ 其中 :& \\ p &:每次暴击的概率\\ k 是变量 &,表示第 k 次暴击\\ \triangle k &: k 增加的步长\\ (N_{Atk} − k + 1) &:表示试验总次数 \\ \end{align*} E保底暴击=k=10∑NAtk(NAtk−k其中:pk是变量△k(NAtk−k+1)+1)⋅((1−p)k−1⋅p)⋅△k:每次暴击的概率,表示第k次暴击:k增加的步长:表示试验总次数
简单验证
笔者经过简单的验证,发现“自然暴击”和“保底暴击”的数学期望加起来,总是与验证结果有些偏差,总体来说会高一点。
这是为什么呢?
猜想
在触发“保底暴击”时,可能此处攻击本来就会发生暴击,导致了重复计算。
一种符合直觉的猜想是:只要让保底暴击的概率乘以未暴击的概率也就是 ( 1 − p ) (1 - p) (1−p),就可以消除重复部分。
多余的“暴击率”
上一篇文章中,笔者提到过“多出来的 2.5%”,下面就是这部分多余的“暴击率”的计算过程。
假设暴击率为 0.2,连续 9 次未暴击后触发“保底暴击”,攻击 100000 次,暴击次数的数学期望为:
E 暴击数 = N A t k ⋅ p + ∑ k = 10 N A t k ( N A t k − k + 1 ) ⋅ ( ( 1 − p ) k − 1 ⋅ p ) ⋅ △ k ⋅ ( 1 − p ) = 100000 × 0.2 + ∑ k = 10 100000 ( 100000 − k + 1 ) × ( ( 1 − 0.2 ) k − 1 × 0.2 ) × △ k × ( 1 − 0.2 ) ≈ 22405.56 其中: p = 0.2 :每次暴击的概率 k 是变量 ,表示第 k 次暴击 △ k = 10 : k 增加的步长 ( 100000 − k + 1 ) :表示试验总次数 \begin{align*} E_{暴击数} = N_{Atk} · p + \sum_{k = 10}^{N_{Atk}} (N_{Atk} − k &+ 1) · ((1 - p)^{k - 1} · p) · \triangle k · (1 - p) \\ = 100000 \times 0.2 + \sum_{k = 10}^{100000} (100000 − k &+ 1) \times ((1 - 0.2)^{k - 1} \times 0.2) \times \triangle k \times (1 - 0.2) \\ \approx 22405.56\\ \\ 其中 :& \\ p = 0.2 &:每次暴击的概率\\ k 是变量 &,表示第 k 次暴击\\ \triangle k = 10 &: k 增加的步长\\ (100000 − k + 1) &:表示试验总次数 \\ \end{align*} E暴击数=NAtk⋅p+k=10∑NAtk(NAtk−k=100000×0.2+k=10∑100000(100000−k≈22405.56其中:p=0.2k是变量△k=10(100000−k+1)+1)⋅((1−p)k−1⋅p)⋅△k⋅(1−p)+1)×((1−0.2)k−1×0.2)×△k×(1−0.2):每次暴击的概率,表示第k次暴击:k增加的步长:表示试验总次数
消除重复部分之后的这部分概率,就是上一篇文章中提到的——多余的“暴击率”(并不是多了 2.5%,而是 2.4%)。
分解公式
为了方便理解,也方便在程序中应用,可以将该公式拆成几个部分;
还可以进行适当的化简,比如最后的 ( 1 − p ) (1 - p) (1−p) 可以乘到 ( 1 − p ) k − 1 (1 - p)^{k - 1} (1−p)k−1 上,变成 ( 1 − p ) k (1 - p)^k (1−p)k;
变量 k k k 作为概率的指数,当其大到一定值时,会非常趋近于 0,计算的价值不大,例如可以根据情况取 30 ~ 100 之间的数作为最大值…
P 保底暴击 = ( 1 − p ) k ⋅ p E 保底暴击 = ∑ k = 10 50 ( N A t k − k + 1 ) ⋅ P 保底暴击 ⋅ △ k E 自然暴击 = N A t k ⋅ p E 总暴击 = E 自然暴击 + E 保底暴击 其中: p = 0.2 :每次暴击的概率 k 是变量 ,表示第 k 次暴击 △ k = 10 : k 增加的步长 ( N A t k − k + 1 ) :表示试验总次数 \begin{align*} P_{保底暴击} &= (1 - p)^{k} · p \\ E_{保底暴击} &= \sum_{k = 10}^{50} (N_{Atk} − k + 1) · P_{保底暴击} · \triangle k \\ E_{自然暴击} &= N_{Atk} · p \\ \\ E_{总暴击} &= E_{自然暴击} + E_{保底暴击} \\ \\ 其中 :& \\ p = 0.2 &:每次暴击的概率\\ k 是变量 &,表示第 k 次暴击\\ \triangle k = 10 &: k 增加的步长\\ (N_{Atk} − k + 1) &:表示试验总次数 \\ \end{align*} P保底暴击E保底暴击E自然暴击E总暴击其中:p=0.2k是变量△k=10(NAtk−k+1)=(1−p)k⋅p=k=10∑50(NAtk−k+1)⋅P保底暴击⋅△k=NAtk⋅p=E自然暴击+E保底暴击:每次暴击的概率,表示第k次暴击:k增加的步长:表示试验总次数
应用到“动态平衡概率”算法中
回顾
为了方便阅读,笔者简化对上一篇文章中的公式说明稍作简化:
基本参数:
P :初始概率(目标概率) P D :动态概率(我们要使用的概率) P C :当前概率(当前暴击出现的频率) △ P :概率差值 N A t k :攻击次数 N C r i t :暴击次数 N N C S :连续未暴击次数 \begin{align*} P & :\text{初始概率(目标概率)} \\ P_{D} & :\text{动态概率(我们要使用的概率)} \\ P_{C} & :\text{当前概率(当前暴击出现的频率)} \\ \triangle P & :\text{概率差值} \\ N_{Atk} & :\text{攻击次数} \\ N_{Crit} & :\text{暴击次数} \\ N_{NCS} & :\text{连续未暴击次数} \\ \end{align*} PPDPC△PNAtkNCritNNCS:初始概率(目标概率):动态概率(我们要使用的概率):当前概率(当前暴击出现的频率):概率差值:攻击次数:暴击次数:连续未暴击次数
运算逻辑:
P C = N C r i t N A t k △ P = P − P C P D = ( N A t k ⋅ △ P + P C ) ⋅ ∣ △ P ∣ (由于最后的系数只是用来调整幅度 所以也可以是其他值,如: P D = ( N A t k ⋅ △ P + P C ) ⋅ △ P ) \begin{align*} P_{C} &= \frac{N_{Crit}}{N_{Atk}} \\ \triangle P &= P - P_{C} \\ P_{D} &= \left( N_{Atk} · \triangle P + P_{C} \right) · \sqrt{|\triangle P|} \\ (由于最后的系数只是用来调整幅度 & \\ 所以也可以是其他值,如:P_{D} &= \left( N_{Atk} · \triangle P + P_{C} \right) · \triangle P) \\ \end{align*} PC△PPD(由于最后的系数只是用来调整幅度所以也可以是其他值,如:PD=NAtkNCrit=P−PC=(NAtk⋅△P+PC)⋅∣△P∣=(NAtk⋅△P+PC)⋅△P)
判断逻辑:
找到一个最佳的 N , 用于判断连续 N − 1 次未暴击 : F i n d _ O p t i m a l _ N ( p ) : ( 1 − p ) N ≤ 0.05 随机数生成和暴击判断 : 如果 N N C S < N − 1 ,则生成一个随机数 p ; ﹂如果 p ≤ P D ,则判定为暴击 ﹂否则 未暴击 否则 必然暴击 \begin{align*} \\ 找到一个最佳的 N,\\ 用于判断连续 N - 1 次未暴击 & : \\ Find\_Optimal\_N(p) & : (1 - p) ^ N \leq 0.05 \\ \\ \text{随机数生成和暴击判断} & : \\ & \text{如果 \(N_{NCS}\) \( < N - 1 \),则生成一个随机数 \(p\);} \\ & \text{ ﹂如果 \(p\) \( \leq \) \(P_{D}\),则判定为暴击} \\ & \text{ ﹂否则 未暴击} \\ & \text{否则 必然暴击} \\ \end{align*} 找到一个最佳的N,用于判断连续N−1次未暴击Find_Optimal_N(p)随机数生成和暴击判断::(1−p)N≤0.05:如果 NNCS <N−1,则生成一个随机数 p; ﹂如果 p ≤ PD,则判定为暴击 ﹂否则 未暴击否则 必然暴击
初始值“优化”
我们可以看到上一篇文章的图表中,在一开始时,“动态暴击率”和“当前暴击率”需要在进行多次攻击之后才能大致稳定下来。
如下图所示
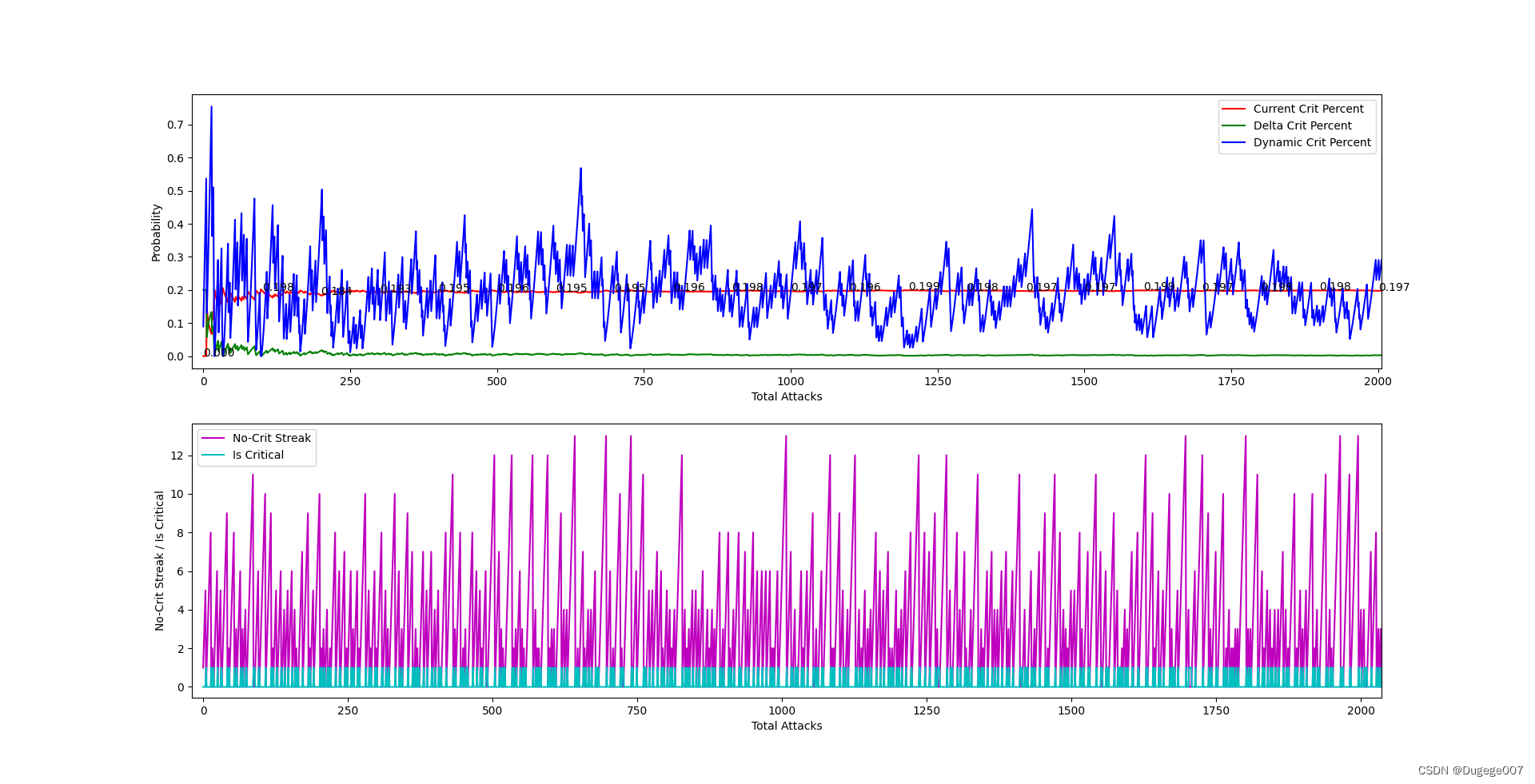
如果赋给“总攻击次数”、“暴击次数”一个较大的初始值,那么在运行程序后“动态暴击率”和“当前暴击率”直接就会是稳定的状态了。
根据前文中关于“多余暴击率的计算”,我们可以轻易求出“动态暴击率”最终的稳定值:
P D ′ = P ⋅ E 自然暴击 E 总暴击 展开并化简: P D ′ = P ⋅ N A t k N A t k + ∑ k = 10 50 ( N A t k − k + 1 ) ⋅ ( 1 − P ) k ⋅ △ k P D ′ :“动态概率”的稳定值 P :初始概率(目标概率) E 自然暴击 :见前文 E 总暴击 :见前文 k :见前文 △ k :见前文 ∵ 要满足“动态概率”的初始值 和稳定值相等,即 P D = P D ′ ∴ ( N A t k ⋅ ( P − N C r i t N A t k ) + N C r i t N A t k ) ⋅ ( P − N C r i t N A t k ) = P ⋅ N A t k N A t k + ∑ k = 10 50 ( N A t k − k + 1 ) ⋅ ( 1 − P ) k ⋅ △ k 将初始值 N A t k = 100000 , P = 0.2... 代入到上式 ( 100000 × ( 0.2 − N C r i t 100000 ) + N C r i t 100000 ) × ( 0.2 − N C r i t 100000 ) = 0.2 × 100000 100000 + 22405.56 ( N C r i t ) 2 + 10000 N C r i t = 200000000 − 1000000000 102405.56 解得: N C r i t = 19872.3 或 20127.9 (一元二次方程求解) 根据题意, N C r i t 不能大于 20000 ,所以舍弃 20127.9 ∴ N C r i t = 19872.3 \begin{align*} P_{D}' &= P · \frac{E_{自然暴击}}{E_{总暴击}} \\ 展开并化简: P_{D}' &= P · \frac{N_{Atk}}{N_{Atk} + \sum_{k = 10}^{50} (N_{Atk} − k + 1) · (1 - P)^{k} · \triangle k} \\ \\ P_{D}' &:“动态概率”的稳定值 \\ P &:初始概率(目标概率) \\ E_{自然暴击} &:见前文 \\ E_{总暴击} &:见前文 \\ k &:见前文 \\ \triangle k &:见前文 \\ \\ \because 要满足“动态概率”的初始值&和稳定值相等,即 P_{D} = P_{D}' \\ \therefore (N_{Atk} · (P - \frac{N_{Crit}}{N_{Atk}}) + \frac{N_{Crit}}{N_{Atk}}) · (P - \frac{N_{Crit}}{N_{Atk}}) &= P · \frac{N_{Atk}}{N_{Atk} + \sum_{k = 10}^{50} (N_{Atk} − k + 1) · (1 - P)^{k} · \triangle k} \\ \\ 将初始值 N_{Atk} = 100000 &,P = 0.2... 代入到上式 \\ (100000 \times (0.2 - \frac{N_{Crit}}{100000}) + \frac{N_{Crit}}{100000}) \times (0.2 - \frac{N_{Crit}}{100000}) &= 0.2 \times \frac{100000}{100000 + 22405.56} \\ (N_{Crit})^{2} + 10000N_{Crit} &= 200000000 - \frac{1000000000}{102405.56} \\ 解得: N_{Crit} &= 19872.3 或 20127.9(一元二次方程求解) \\ 根据题意,N_{Crit} &不能大于 20000,所以舍弃 20127.9 \\ \therefore N_{Crit} &= 19872.3 \\ \end{align*} PD′展开并化简:PD′PD′PE自然暴击E总暴击k△k∵要满足“动态概率”的初始值∴(NAtk⋅(P−NAtkNCrit)+NAtkNCrit)⋅(P−NAtkNCrit)将初始值NAtk=100000(100000×(0.2−100000NCrit)+100000NCrit)×(0.2−100000NCrit)(NCrit)2+10000NCrit解得:NCrit根据题意,NCrit∴NCrit=P⋅E总暴击E自然暴击=P⋅NAtk+∑k=1050(NAtk−k+1)⋅(1−P)k⋅△kNAtk:“动态概率”的稳定值:初始概率(目标概率):见前文:见前文:见前文:见前文和稳定值相等,即PD=PD′=P⋅NAtk+∑k=1050(NAtk−k+1)⋅(1−P)k⋅△kNAtk,P=0.2...代入到上式=0.2×100000+22405.56100000=200000000−102405.561000000000=19872.3或20127.9(一元二次方程求解)不能大于20000,所以舍弃20127.9=19872.3
由于计算过程太过繁琐,下面是笔者通过试验总结的“初始攻击数”与对应“初始暴击数”的对照表:
(可能与运算结果稍有偏差,但在图像上接近稳定值)
# 当 初始暴击率 为 0.2 时就,需满足下列条件才能在一开始就获得稳定的初始值:
# 总攻击次数初始值 为 10 时,总暴击次数 约为 2 - 1
# 总攻击次数初始值 为 100 时,总暴击次数 约为 20 - 4
# 总攻击次数初始值 为 1000 时,总暴击次数 约为 200 - 14
# 总攻击次数初始值 为 10000 时,总暴击次数 约为 2000 - 43
# 总攻击次数初始值 为 100000 时,总暴击次数 约为 20000 - 137
# 总攻击次数初始值 为 1000000 时,总暴击次数 约为 200000 - 435
# 总攻击次数初始值 为 10000000 时,总暴击次数 约为 2000000 - 1370
# 总攻击次数初始值 为 100000000 时,总暴击次数 约为 20000000 - 4350
# 总攻击次数初始值 为 1000000000 时,总暴击次数 约为 200000000 - 13700
# 当 初始暴击率 为 0.5 时,需满足下列条件才能在一开始就获得稳定的初始值:
# 总攻击次数初始值 为 10 时,总暴击次数 约为 5 - 2
# 总攻击次数初始值 为 100 时,总暴击次数 约为 50 - 7
# 总攻击次数初始值 为 1000 时,总暴击次数 约为 500 - 22
# 总攻击次数初始值 为 10000 时,总暴击次数 约为 5000 - 69
# 总攻击次数初始值 为 100000 时,总暴击次数 约为 50000 - 219
# 总攻击次数初始值 为 1000000 时,总暴击次数 约为 500000 - 692
# 总攻击次数初始值 为 10000000 时,总暴击次数 约为 5000000 - 2194
# 总攻击次数初始值 为 100000000 时,总暴击次数 约为 50000000 - 6924
# 总攻击次数初始值 为 1000000000 时,总暴击次数 约为 500000000 - 21940
# 当 初始暴击率 为 0.8 时,需满足下列条件才能在一开始就获得稳定的初始值:
# 总攻击次数初始值 为 10 时,总暴击次数 约为 8 - 3
# 总攻击次数初始值 为 100 时,总暴击次数 约为 80 - 9
# 总攻击次数初始值 为 1000 时,总暴击次数 约为 800 - 27
# 总攻击次数初始值 为 10000 时,总暴击次数 约为 8000 - 87
# 总攻击次数初始值 为 100000 时,总暴击次数 约为 80000 - 274
# 总攻击次数初始值 为 1000000 时,总暴击次数 约为 800000 - 870
# 总攻击次数初始值 为 10000000 时,总暴击次数 约为 8000000 - 2740
# 总攻击次数初始值 为 100000000 时,总暴击次数 约为 80000000 - 8700
# 总攻击次数初始值 为 1000000000 时,总暴击次数 约为 800000000 - 27400
虽然还是能看出一些规律,但笔者能力有限,目前还无法优雅地总结出这其中的规律。
目前需要在每次暴击率发生变化时重新计算一次,这样在数值过大时,可能还会有丢失一些精度,导致计算出问题…将“动态概率”在一开始就稳定下来这种做法,目前看来有点得不偿失…
所以搞了半天,这优化还不如不优化?
虽然失败了,但至少我们知道了如何求出多余的“暴击率”,也算是有点收获吧。
直接取“动态暴击率”的稳定值?
既然我们可以求出“动态暴击率”的稳定值,那么当有“保底暴击”这样的设定时,直接取“动态暴击率”的稳定值作为暴击率不就好了吗?
通过对上文内容的分析,我们不难发现,这个“稳定值”其实也是一个变量,需要不断计算,这种方式也很耗费性能。
目前来看,直接取“动态暴击率”的稳定值这种方案,是不可行的。
“镜像修正”算法
经过一段时间的思考和尝试,笔者认为最好用的,其实是上篇文章中提到“镜像修正”算法的最初形式:
P C = N C r i t N A t k △ P = P − P C P D = N A t k ⋅ △ P + P C 其中: P :初始概率(目标概率) P D :动态概率(我们要使用的概率) P C :当前概率(当前暴击出现的频率) △ P :概率差值 N A t k :攻击次数 N C r i t :暴击次数 \begin{align*} P_{C} &= \frac{N_{Crit}}{N_{Atk}} \\ \triangle P &= P - P_{C} \\ P_{D} &= N_{Atk} · \triangle P + P_{C} \\ \\ 其中 :& \\ P & :\text{初始概率(目标概率)} \\ P_{D} & :\text{动态概率(我们要使用的概率)} \\ P_{C} & :\text{当前概率(当前暴击出现的频率)} \\ \triangle P & :\text{概率差值} \\ N_{Atk} & :\text{攻击次数} \\ N_{Crit} & :\text{暴击次数} \\ \end{align*} PC△PPD其中:PPDPC△PNAtkNCrit=NAtkNCrit=P−PC=NAtk⋅△P+PC:初始概率(目标概率):动态概率(我们要使用的概率):当前概率(当前暴击出现的频率):概率差值:攻击次数:暴击次数
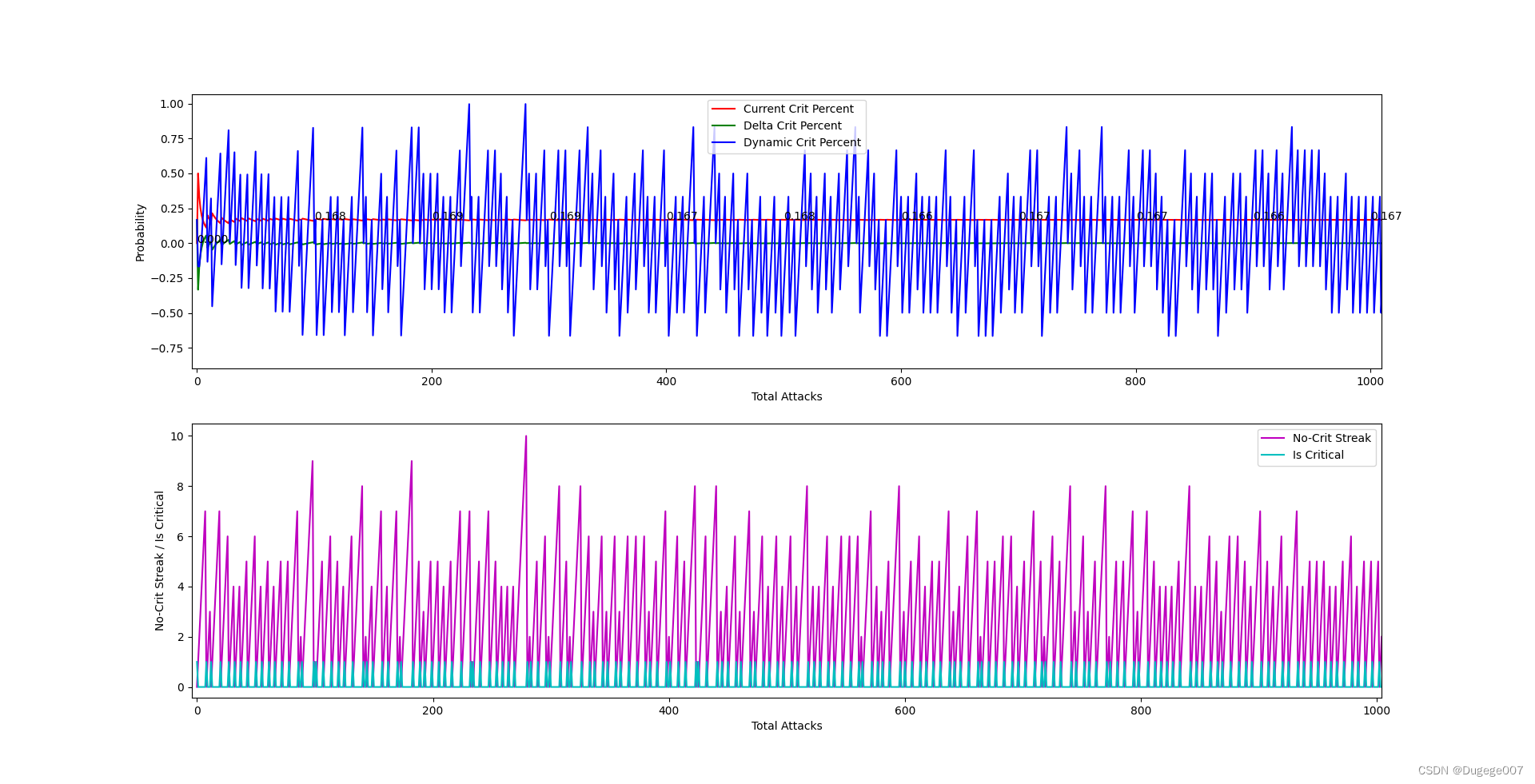
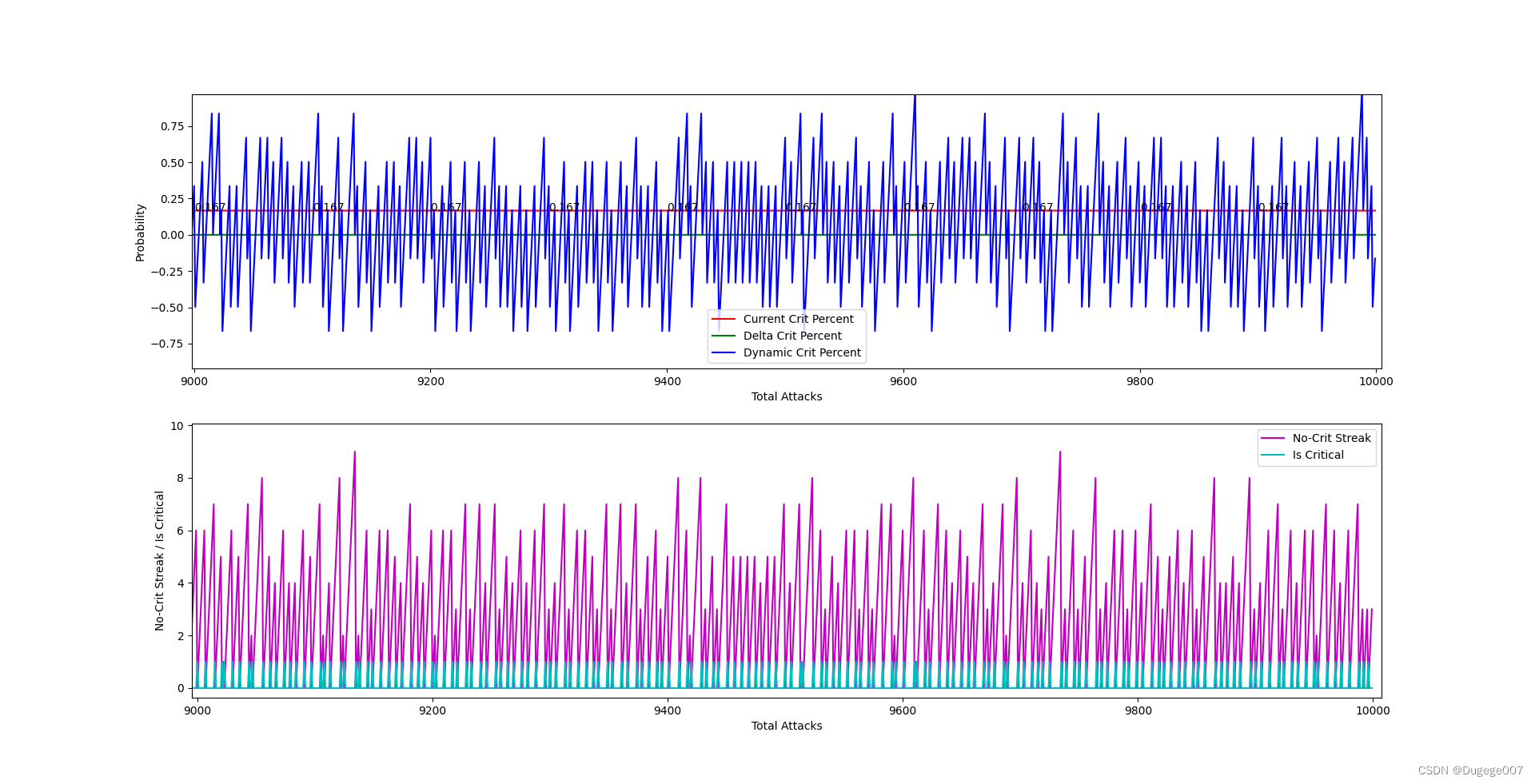
相比最后版本的“动态平衡概率”算法,这一版算法只是去掉了最后的系数。
这种暴击分布非常均匀的算法,应该会让玩家感到很“舒服”。
代码相较上一篇文章的最后版本,只有这一行发生了变化:
# 计算动态暴击率
dynamicCritPercent = attackTotalCount * deltaCritPercent + currentCritPercent
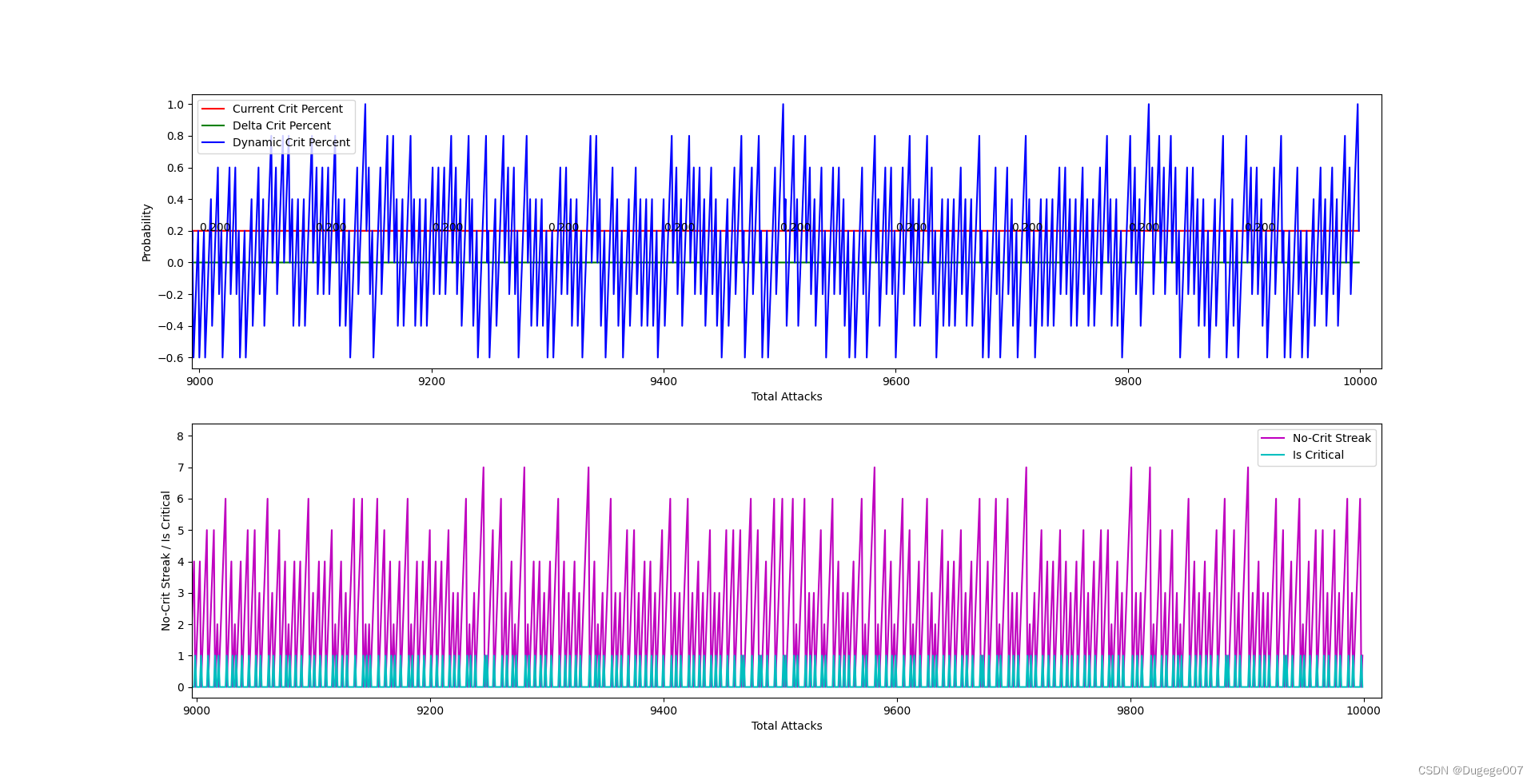
初始概率为 0.2 的输出结果
前 1000 次
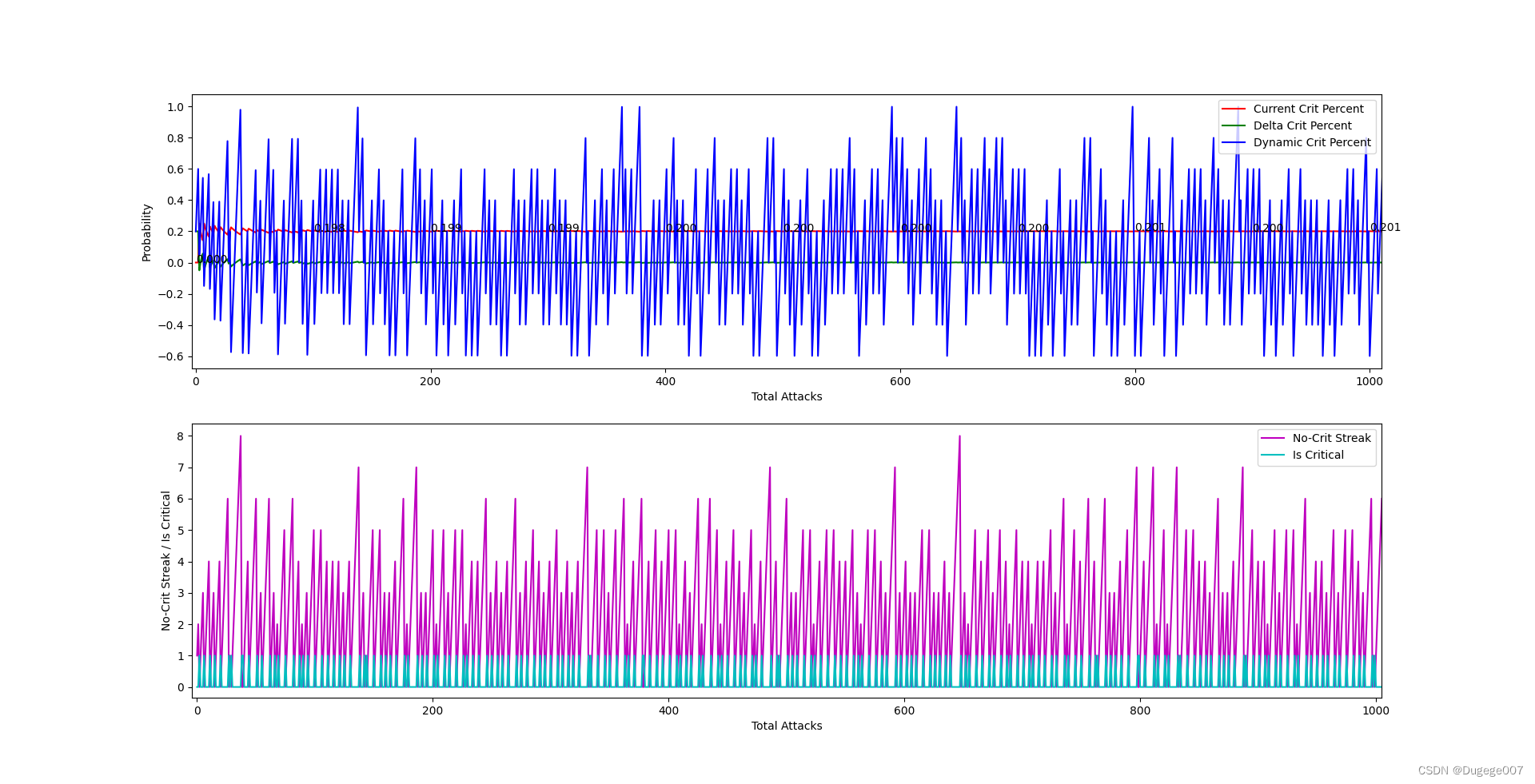
9000 ~ 10000次
初始概率为 0.5 的输出结果
前 500 次
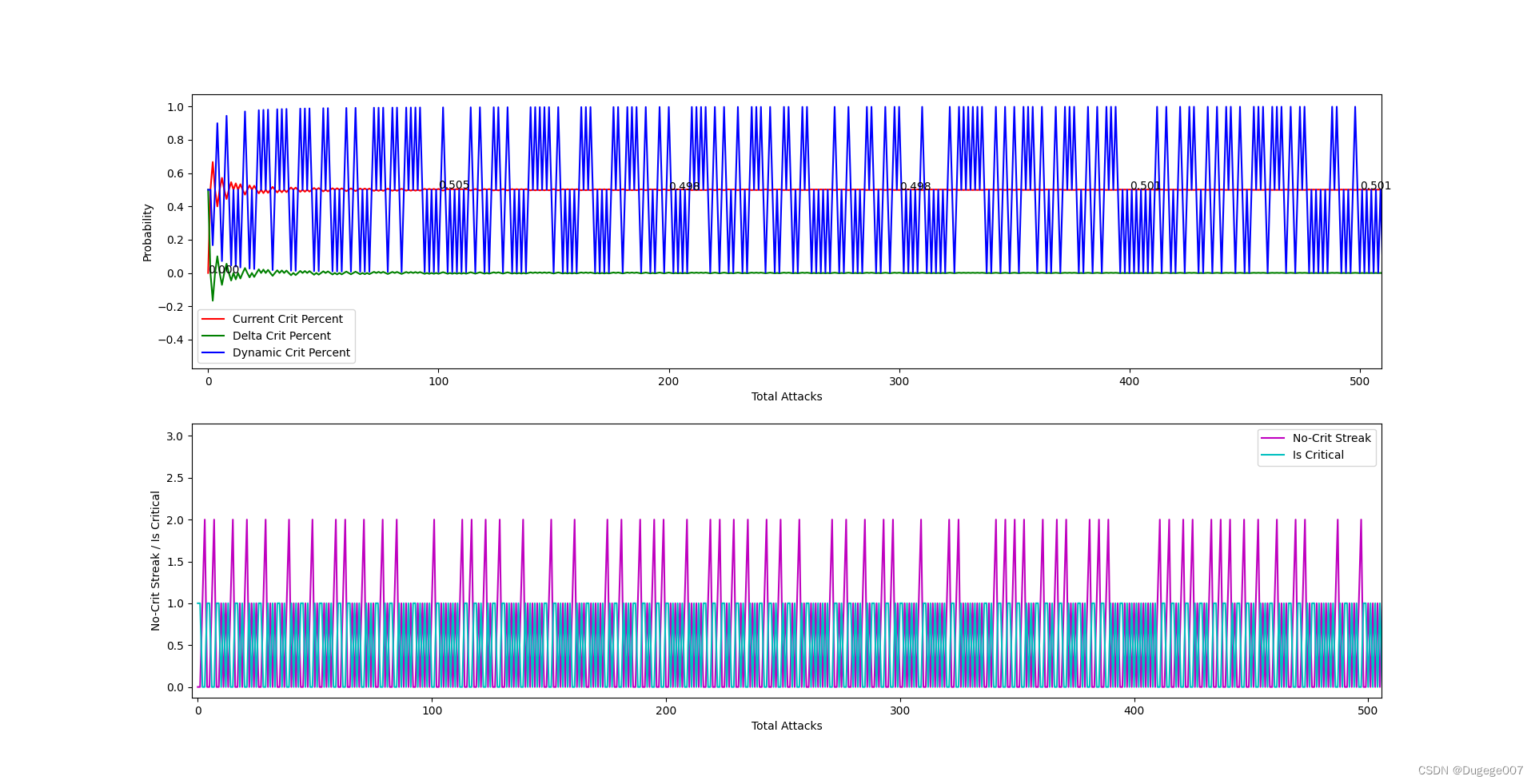
9500 ~ 10000次
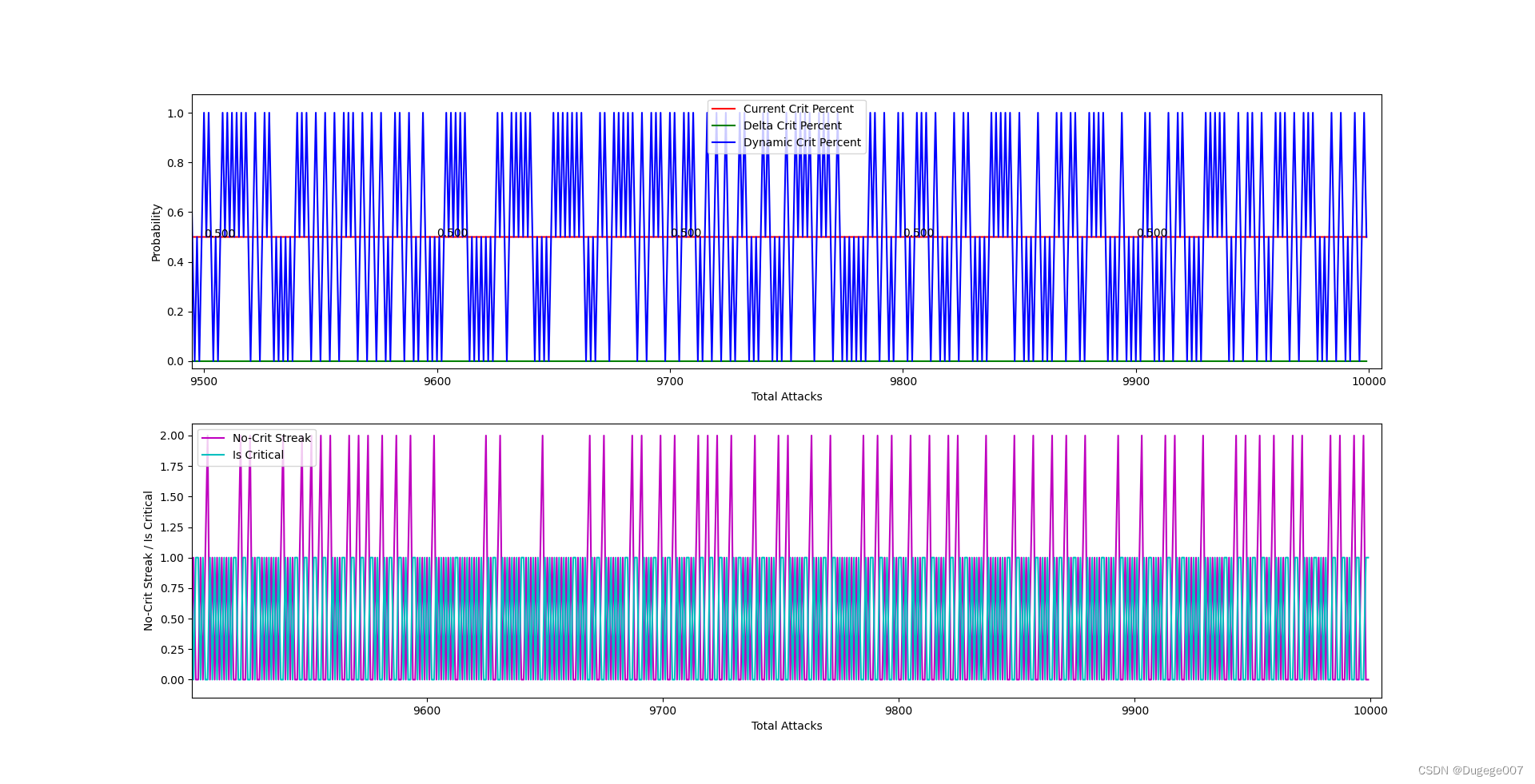
初始概率为 0.166667 的输出结果
前 1000 次
9000 ~ 10000次
总结
使用场景
在不同的场景下,我们可以选用不同的计算概率的方式。
例如在竞技类的游戏中,我们会希望暴击率出现的频次比较稳定,那么可以使用“镜像修正”算法(可以加上一定的限制,让玩家对连续多次未暴击后,下次是否触发暴击有一定的预期)。
在肉鸽游戏、抽卡游戏等,有随机性但是没有竞技性的游戏中,可以用“动态平衡概率”算法,让抽中的分布不那么平均,同时也有保底,这样会显得更加“自然”。
当然,开发者也可以不加任何的“保底”。用“真随机”让玩家感受到概率的“残酷”…
吉祥话
最后,感谢您看到这里,祝您永远幸运,永远用不到“保底”!
也欢迎大佬们给出批评建议,再次感谢!