HMM之前向算法

HMM-前向算法

第一章：

假定现在隐含态是s1,s2,s3；观测状态是A,B

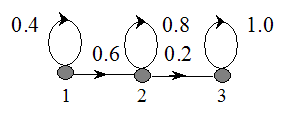
隐含态之间的转移情况如下图1:

图1

上图1,2,3对应的就是隐含态s1,s2,s3之间的转移情况，然后他们之间的输出状态A,B之间的概率如下表

现在要计算观测序列是O={ABAB}的概率是多少？

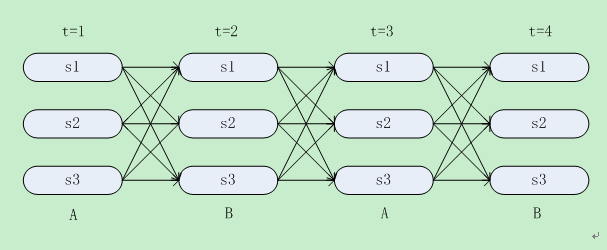
把上面问题抽象成如下网络模型:

图2

要计算O={ABAB}的概率，即P(ABAB|HMM) = P(ABAB|s1,s1,s1,s1)+ P(ABAB|s2,s1,s1,s1)+.........+......

因此，要计算概率，需要计算3^4种可能性的总和！用这种方式计算，对于序列特别长的情况，开销巨大，因此考虑用概率的时间不变形来减少复杂度。

第二章

如前面所说的即为穷举搜索，开销很大。下面利用概率的时间不变性，来减小复杂度。

给定一个HMM，我们将递归的考虑观测序列的概率。首先引出一个概念:局部概率(partialprobability)，它是达到图2网络中某一观测状态的概率。

假设一个T-长观测序列:

根据上图2，t=2时位于"s2"的局部概率通过如下路径计算得出：

图3

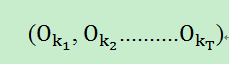
我们定义t时刻位于状态j的局部概率为α_t(j)——这个局部概率计算如下：

α_t(j)= P( 观察状态 | 隐藏状态j ) * P(t时刻所有指向j状态的路径)

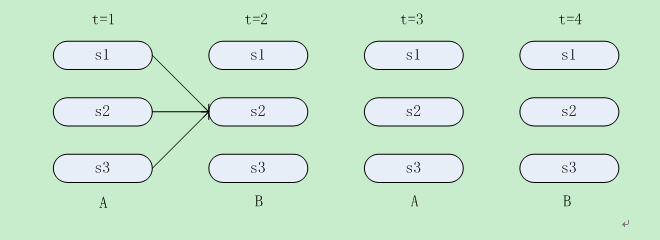
对于最后的观测状态，其局部概率包括了通过所有可能的路径到达这些状态的概率。对于图2，最终的局部概率通过如下路径得到:

图4

从图4中，如果计算出来t=4时所有局部概率，并且将其求和，就等价于是计算出了O={ABAB}的观测状态的概率。

当t=1时，局部概率是多少呢？

由于在t=1时，不存在在此之前的状态,根据公式:

α_t(j)= P( 观察状态 | 隐藏状态j ) * P(t时刻所有指向j状态的路径)

在公式的乘积的右边等式,不存在指向当前状态的路径，因此，位于当前状态的概率就是初始概率，因此在t=1时，局部概率等于初始概率乘以输出概率，即

当t>1时，计算局部概率:

α_t(j)= P( 观察状态 | 隐藏状态j ) * P(t时刻所有指向j状态的路径)

对于公式右侧的第一项，P( 观察状态 | 隐藏状态j )是输出概率，在本例子中是已知的；重点是计算后面那一项:P(t时刻所有指向j状态的路径)。

如图2所示，在t=2时，指向s2的所有路径有：s1->s2,s2->s2,s3->s2;状态与状态之间有转移概率,而在t=1时刻的局部概率，在此之前是已经计算出来了,因此，对于图2，在t=2时，位于s2状态的局部概率是:

解释一下上述符号:

n:隐含状态数

a_j2：从隐含s_j状态转移到隐含状态s₂的转移概率(j=1,2,3)

α_t(j): t=1时刻的隐含状态s_j的局部概率。

因此:根据递归的思想，可以得到t时刻(t>1)的局部概率是:

因此:对于最开始提出的概率计算，观测序列是O={ABAB}的概率是多少？

先计算t=1时刻的局部概率α₁

然后根据局部概率α₁，转移概率a，输出概率b，计算t=2时刻的局部概率:α₂

然后根据局部概率α₂，转移概率a，输出概率b，计算t=3时刻的局部概率:α₃

然后根据局部概率α₃，转移概率a，输出概率b，计算t=4时刻的局部概率:α₄

α₄的分别是

α₄(1)(t=4时，s1输出B的概率),

α₄(2)(t=4时，s2输出B的概率),

α₄(3)(t=4时，s3输出B的概率).

因此:要计算O={ABAB}的概率是多少，就是α₄(1)+ α₄(2)α₄(3).

第三章

如下为示例代码：

#! /usr/bin/env python
#! -*- coding=utf-8 -*-

from numpy import *
import numpy as np
import random
import copy

#HMM-forward算法
def hmm_forward():
	Nstate = 3
	Nobs = 2
	T = 4
	init_prob = [1.0,0.0,0.0]
	trans_prob = np.array([[0.4,0.6,0.0],[0.0,0.8,0.2],[0.0,0.0,1.0]])
	emit_prob = np.array([[0.7,0.3],[0.4,0.6],[0.8,0.2]])
	obs_seq = [0,1,0,1] #(ABAB)
	#单独计算t=1时刻的局部概率
	partial_prob = zeros((Nstate,T))
	for i in range(Nstate):
		partial_prob[i,0] = init_prob[i] * emit_prob[i,obs_seq[0]]	
	#计算t>1时刻的局部概率
	for t in range(1,T,1):		
		for i in range(Nstate):
			tmp = 0
			for j in range(Nstate):
				tmp = tmp + partial_prob[j,t-1] * trans_prob[j,i]
			partial_prob[i,t] = tmp * emit_prob[i,obs_seq[t]]	
	print (partial_prob[:,T-1]).sum()
if __name__ == '__main__':
	hmm_forward()