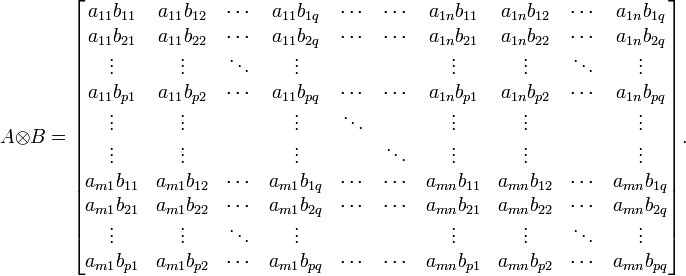克罗内克积 Kronecker product

http://www.docin.com/p-1286196923.html比较详细

如果A是一个 m × n 的矩阵，而B是一个 p × q 的矩阵，克罗内克积则是一个 mp × nq 的分块矩阵

更具体地可表示为

双线性结合律

克罗内克积是 张量积的特殊形式，因此满足双线性与 结合律：

其中， A, B和 C是矩阵，而 k是常量。

克罗内克积不符合 交换律：通常，

   

不同于

   

。

 

和

   

是置换等价的，也就是说，存在 置换矩阵 P和 Q，使得

如果 A和 B是方块矩阵，则

   

和

   

甚至是置换 相似的，也就是说，我们可以取 P= Q。

混合乘积性质

如果 A、 B、 C和 D是四个矩阵，且矩阵乘积 AC和 BD存在，那么：

这个性质称为“混合乘积性质”，因为它混合了通常的矩阵乘积和克罗内克积。于是可以推出，

   

是 可逆的 当且仅当 A和 B是可逆的，其逆矩阵为：

克罗内克和

如果 A是 n× n矩阵， B是 m× m矩阵，

   

表示 k× k单位矩阵，那么我们可以定义克罗内克和

   

为：

与抽象张量积

矩阵的克罗内克积对应于线性映射的抽象张量积。特别地，如果向量空间 V、 W、 X和 Y分别具有基{v 1, ... , v m}、 {w 1, ... , w n}、{x 1, ... , x d}和{y 1, ... , y e}，且矩阵 A和 B分别在恰当的基中表示线性变换 S: V→ X和 T: W→ Y，那么矩阵 A⊗ B表示两个映射的张量积 S⊗ T: V⊗ W→ X⊗ Y，关于 V⊗ W的基{v 1⊗ w 1, v 1⊗ w 2, ... , v 2⊗ w 1, ... , v m⊗ w n}和 X⊗ Y的类似基。 [2]  

与图的乘积

两个 图的 邻接矩阵的克罗内克积是它们的张量积图的邻接矩阵。两个图的邻接矩阵的克罗内克和，则是它们的笛卡儿积图的邻接矩阵。 [3]  

转置

克罗内克积转置运算符合分配律：