重点

界定一个节点的输入和输出
$z$ 是激励函数的输出

Backpropagation算法(BP)是深度学习的基础,没有BP算法就没有神经网络,也不会有现在如火如荼的深度学习. BP算法并不仅仅适用于神经网络,对于任意系统,抽象成输入/输出/参数三个部分,如果输出对每个参数的导数已知,那么可以用BP算法把该系统调节到最优. 当然上述结论只在理论上成立,实践中会遇到各种问题,比如梯度爆炸/消失等数值问题. 本文通过一个简单的例子,介绍BP算法的推导过程.

卷积网络出现之前,神经网络有若干层组成,每个层有若干节点组成,层和层之间全连接,如下是 $k$ 层的第 $j$ 个节点节点示意图:

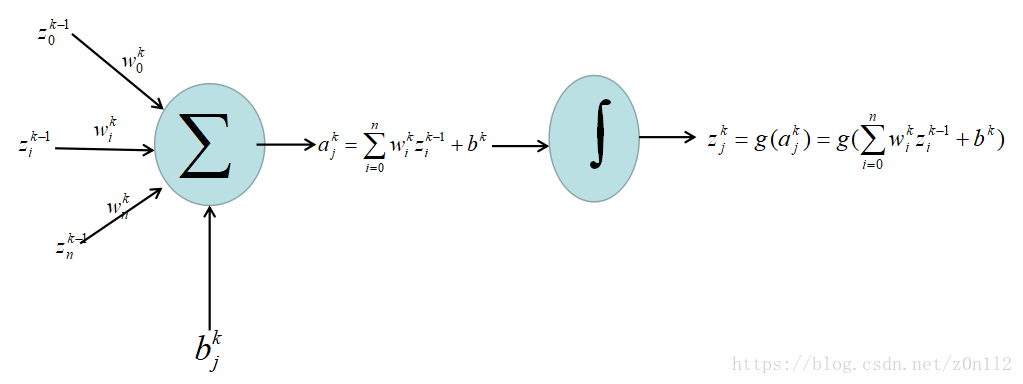
这里写图片描述

为了后续推导方便,这里把一个节点拆分成两个部分
* 求和
上图左侧的 $\sum$ 符号代表的部分,其输入 ${z_i^{k-1}}$ $i=0,1,2,...,n$ 是前一层 $k-1$ 层的 $n$ 个输出, $w_i^k$ 是当前层的权重参数, $b_j^k$ 是当前节点的偏置参数,其输出是 $a_j^k=\sum_{i=0}^{n}w_i^kz_i^{k-1}+b_j^k$ , 这是一个临时变量,方便后续推导
* 激励
上图右侧的 $\int$ 符号代表激励函数,深度学习之前常见的的sigmoid/tanh,深度学习兴起后比较常见的是relu,激励函数必须是可导的,改进方向一般有
1. 前向传播时对数据的压缩能力
sigmoid把数据压缩到 $[0,1]$ ,比relu要好.压缩数据可以避免数据爆炸,加深网络层数
2. 后向传播时对梯度的保持能力
sigmoid之所以被relu替代,就是relu梯度为1(输入大于0时),不会压缩梯度,反向传播时更加有利

假设已知网络输出 $J$ 对 $z^k_j$ 的导数 $\delta _j^k =\frac{dJ}{dz^k_j}$ ,BP反向传播时有一下三个值需要求取

$J$ 对 $z^{k-1}_i$ 的导数 $\delta _i^{k-1} =\frac{dJ}{dz^{k-1}_i}$
链式法则

$\frac{d J}{d z_{i}^{k - 1}} = \frac{d J}{d z_{j}^{k}} \frac{d z_{j}^{k}}{d z_{i}^{k - 1}} = δ_{j}^{k} \frac{d z_{j}^{k}}{d z_{i}^{k - 1}} = δ_{j}^{k} \frac{d z_{j}^{k}}{d a_{j}^{k}} \frac{d a_{j}^{k}}{z_{i}^{k - 1}} = δ_{j}^{k} ▽ g (a_{j}^{k}) \frac{d a_{j}^{k}}{z_{i}^{k - 1}} = δ_{j}^{k} ▽ g (a_{j}^{k}) w_{i}^{k}$ $\frac{dJ}{dz^{k-1}_i}=\frac{dJ}{dz^{k}_j}\frac{dz^k_j}{dz^{k-1}_i}=\delta _j^{k}\frac{dz^k_j}{dz^{k-1}_i}=\delta _j^{k}\frac{dz^k_j}{da^{k}_j}\frac{da^k_j}{z^{k-1}_i}=\delta _j^{k}\bigtriangledown g(a^k_j)\frac{da^k_j}{z^{k-1}_i}=\delta _j^{k}\bigtriangledown g(a^k_j)w^k_i$
所以导数 $\delta$ 从 $k$ 层反向传播到 $k-1$ 层,如下所示
$δ_{i}^{k - 1} = δ_{j}^{k} ▽ g (a_{j}^{k}) w_{i}^{k}$ $\delta _i^{k-1}=\delta _j^{k}\bigtriangledown g(a^k_j)w^k_i$
$J$ 对 $w^{k}_i$ 的导数
计算这个不是为了反向传播,而是为了应用梯度下降算法更新 $w^k_i$ , 同样利用链式法则

$\frac{d J}{d w_{i}^{k}} = \frac{d J}{d z_{j}^{k}} \frac{d z_{j}^{k}}{d w_{i}^{k}} = δ_{j}^{k} \frac{d_{j}^{k}}{d w_{i}^{k}} = δ_{j}^{k} \frac{d z_{j}^{k}}{d a_{j}^{k}} \frac{d a_{j}^{k}}{w_{i}^{k}} = δ_{j}^{k} ▽ g (a_{j}^{k}) \frac{d a_{j}^{k}}{w_{i}^{k}} = δ_{j}^{k} ▽ g (a_{j}^{k}) z_{i}^{k - 1}$ $\frac{dJ}{dw^{k}_i}=\frac{dJ}{dz^{k}_j}\frac{dz^k_j}{dw^{k}_i}=\delta _j^{k}\frac{d^k_j}{dw^{k}_i}=\delta _j^{k}\frac{dz^k_j}{da^{k}_j}\frac{da^k_j}{w^{k}_i}=\delta _j^{k}\bigtriangledown g(a^k_j)\frac{da^k_j}{w^{k}_i}=\delta _j^{k}\bigtriangledown g(a^k_j)z^{k-1}_i$
$J$ 对 $b^{k}_j$ 的导数
和上面类似,为了应用梯度下降算法更新 $b^k_j$ ,继续链式法则

$\frac{d J}{d b_{j}^{k}} = \frac{d J}{d z_{j}^{k}} \frac{d z_{j}^{k}}{d b_{j}^{k}} = δ_{j}^{k} \frac{d_{j}^{k}}{d b_{j}^{k}} = δ_{j}^{k} \frac{d z_{j}^{k}}{d a_{j}^{k}} \frac{d a_{j}^{k}}{b_{j}^{k}} = δ_{j}^{k} ▽ g (a_{j}^{k}) \frac{d a_{j}^{k}}{b_{j}^{k}} = δ_{j}^{k} ▽ g (a_{j}^{k})$ $\frac{dJ}{db^{k}_j}=\frac{dJ}{dz^{k}_j}\frac{dz^k_j}{db^{k}_j}=\delta _j^{k}\frac{d^k_j}{db^{k}_j}=\delta _j^{k}\frac{dz^k_j}{da^{k}_j}\frac{da^k_j}{b^{k}_j}=\delta _j^{k}\bigtriangledown g(a^k_j)\frac{da^k_j}{b^{k}_j}=\delta _j^{k}\bigtriangledown g(a^k_j)$

BP反向传播公式推导

重点

猜你喜欢