还是用前向算法的图, 然后仔细一看分类输出, 发现好像错了, 这该如何去反向修改权值呢? 因其是网络结构, 改变一点, 必然会引起一连串的改动, 这个过程, 如何来描述呢?
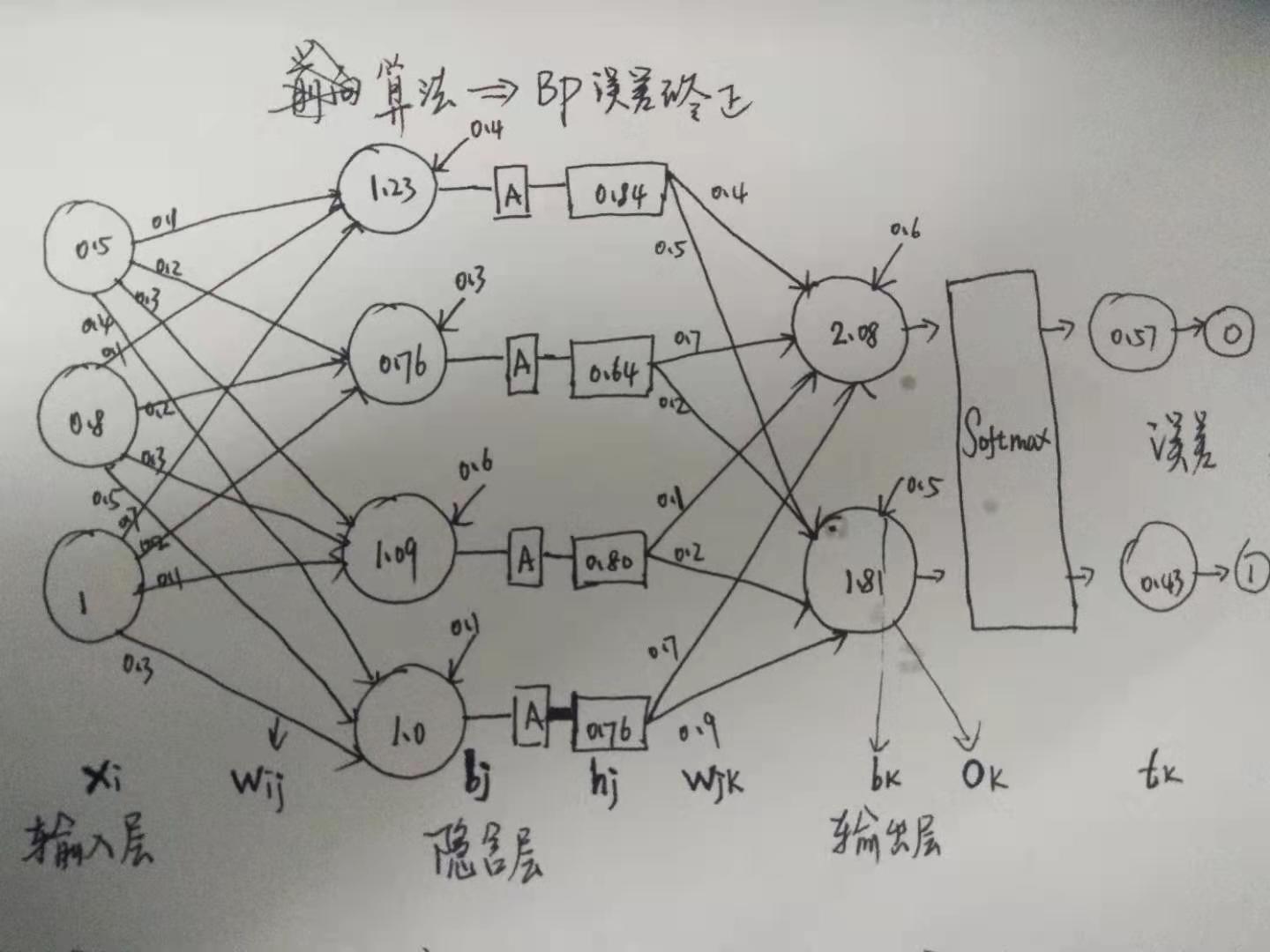
数学推导
声明变量
首先,且极为重要的一步就是, 变量定义. 跟写代码的逻辑其实是差不多的.
声明: 以下用的的字母, 均为向量(W是矩阵), 带了下标,就是其 某个分量, 是个实数值
\(x_i\) 表示 输入层 的第 i 个节点(特征) 的值
\(w_{ij}\) 表示 第 i 个节点中, 第 j 个分量的权值, W 是一个矩阵.
\(b_j\) 表示 某隐含层第 j 个节点的 偏置 Bias
\(h_j\) 表示 某隐含层 的通过 激活函数得到的 第 j 个节点的 激活值
\(w_{jk}\) 表示 某隐含层第 j 节点的 激活值 的 第 k 个分量的权值, W是一个矩阵
- \(a_k\) 表示 输出层 第 k 个节点的值
\(o_k\) 表示 输出层 经过 Softmax 得到的第 k 个节点 的 观测值
\(t_k\) 表示 最终标记值
感觉, 分量也不太准确, 像 \(w_{ij}\) 描述为 第 i 个节点, 对下一层的 第 j 个节点的权重值, 会更好一点.
推导整体思路
绝大多数的ML算法推导, 套路都是一样的, 始终围绕两个核心的话题:
如何定义损失函数 ?
如何优化损失函数 ?
我渐渐感到, 随着学习经验的累积, ML 其实并不难哦, 当然有前提是 必须熟练编程.
都只是用到了一些, 基础的数学理论而已, 高频率的词汇, 如, 求偏导数(梯度), 向量/矩阵求导, 高斯分布, 极大似然, 泰勒级数展开, 拉格朗日乘子, p范数, 期望与方差, 参数估计, 矩阵分解 ..
其实就是大一, 大二 所学的高等数学基础. 也似乎理解了前段时间, 丘成桐教授的一篇文, 大意是说, 人工智能的数学理论, 30年来都止步不前, 没有任何突破性的进展.
损失函数, 这里其实就是 输出值 和 标记值 误差平方和 呀
\(min \ L = \sum \limits_k \frac {1} {2} (t_k - o_k)^2\)
通过上面的定义, 需要优化的变量有: \(b_k, w_{jk}, b_j, w_{ij}\) 优化算法的套路, 就是对要优化的变量进行 求偏导(梯度), 然后沿着 梯度的 反方向, 通过一个步长, 去调整优化. 使得误差尽可能的小, 就是如此朴素的思想而已, 真的没有创新.
四大公式
这里先不细节, 先走一遍主逻辑, 再细节的来推导每一步是为什么, 这也是我写代码的逻辑, 嗯, 主要怕逻辑混乱哈.
\(\nabla {w_{jk}} = h_j(o_k - t_k) \ ..................(1)\)
为了上公式更加简洁, 将误差记为: \(\delta_k = (o_k - t_k)\)
\(\nabla {b_k} = (o_k - t_k) \ ......................(2)\)
\(\nabla {b_j} = \sum\limits_k \delta_k \ w_{jk} (1+h_j)(1-h_j) \ ... ... (3)\)
\(\nabla {w_{ij}} = x_i \sum \limits _k \delta_k w_{jk} (1+h_j)(1-h_j) \ ...(4)\)
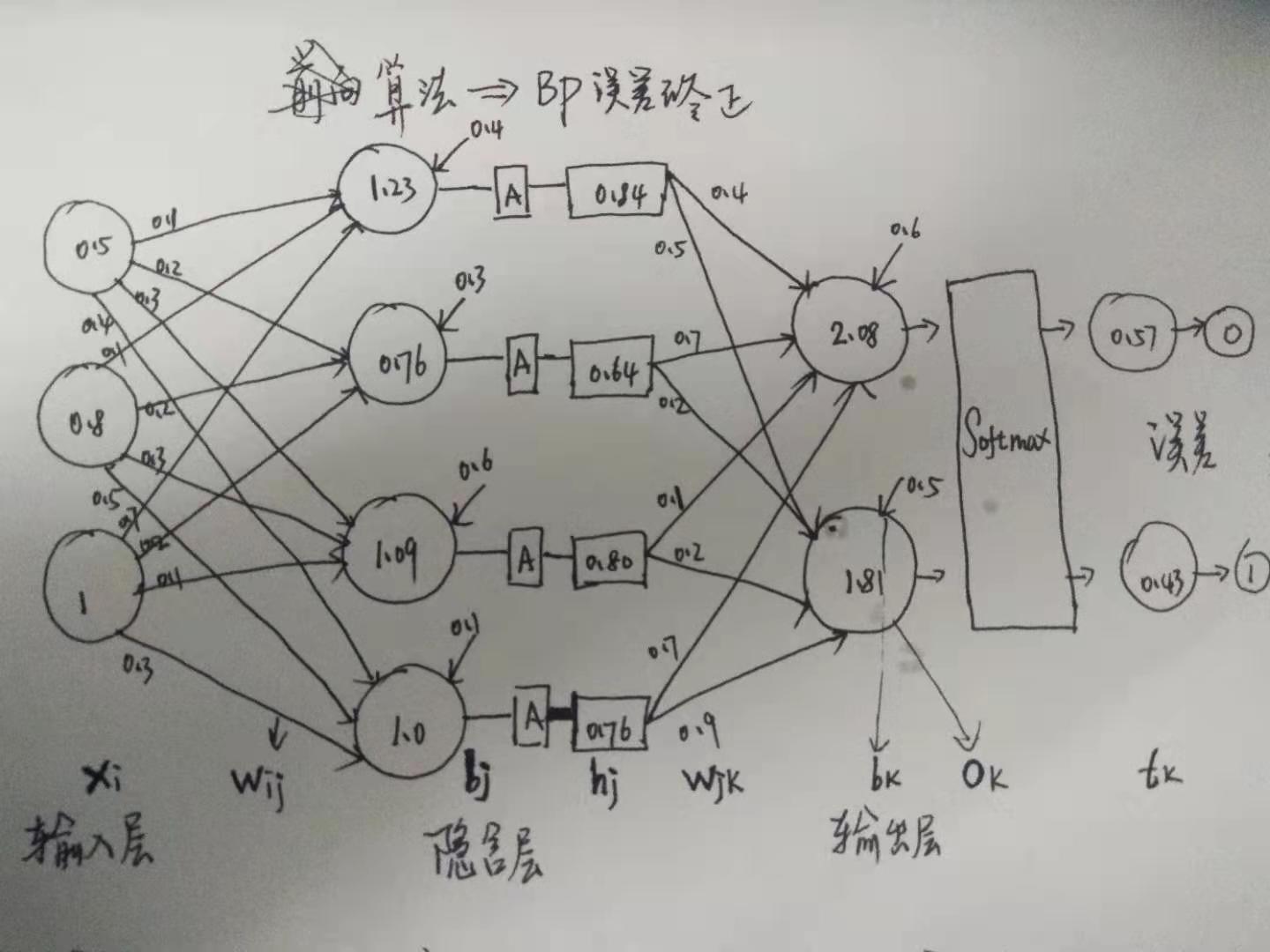
假设就关注一波, 这个 \(w_{ij} = 0.5\) 这个值. (画图, 对每个值, 变量的直观理解, 极为重要哈)
case1: 隐含层权值 \(w_{jk}\) 更新
那, 能够影响到 0.5 的这个值的有: 预测的输出 \(o_k\), 标签值 \(t_k\), 还有它前面一层的激活值 \(h_j\) 根据公式1:
\(\nabla {w_{jk}} = h_j(o_k - t_k) \ ..................(1)\)
\(= 0.84 * (0.57 - 0) = 0.479\)
然后如果要调 0.5 这个参数, Update = 当前参数值 - 梯度 * 学习率
\(= 0.5 - 0.479 * 0.01 = 0.495\) (假设 Learning_rate 或 步长为 0.01)
图上来看, 将 0.5 减小了的话, 输出值 0.57也会变小, 然后会更接近标签值 0
case2: 强化 - 隐含层权值 \(w_{jk}\) 更新
同理, 对于 0.4 的更新也是一样的分析. 首先, 能影响到 0.4的值有, 预测值输出 \(o_k\), 标签值 \(t_k\) , 前一层的激活值 \(h_j\)
\(\nabla {w_{jk}} = h_j(o_k - t_k) \ ..................(1)\)
\(= 0.84 * (0.43-1) = - 0.478\)
假设步长为 0.1
Update = \(0.4 - (-0.478 * 0.1 = 0.447\)
图上来看, 将 0.4 增大了的话, 输出值 0.43 也会增大, 然后更接近 标签值 1
case: 输入层-过渡 隐含层权值 \(w_{ij}\) 更新
同理, 对于左上边第一根线的 0.1, 可能不太直观哦, 瞥一眼公式 (4)
\(\nabla {w_{ij}} = x_i \sum \limits _k \delta_k w_{jk} (1+h_j)(1-h_j) \ ...(4)\)
跟 \(x_i, o_k, t_k, w_{jk}, h_j\) 都是有联系的.
注意理解 \(\sum\) 的作用变量哦, 无关的看作常数即可, 积分也是一样滴
\(= 0.5([(0.57-0) * 0.5] + [(0.43-1)*0.4] * (1+0.84) (1-0.84) \\ =0.0084\)
同样用梯度更新的方式, 假设步长为 0.1.
update = 0.1 - 0.1 * 0.0084 = 0.09916
也就是将这个权重值调整小, 跟着它向前的这条线路呢, 最终的 \(o_t= 0.57\) 也会小, 也恰好接近于我的期望值
推导详细过程
本质上是函数求导的链式法则.
平方误差 + Softmax 的梯度
设 Softmax 的输入向量为 a \(= (a_1, a_2, a_3, ...a_k)^T\), 其中, \(a_i = \sum\limits_j W_{ji} h_j + b_i\)
W是个向量, W_ji 表示前层的第 j 个节点的 第 i个权值. \(W_{ji} h_j\) 是一条线的权值和激活节点的值,相关的所有的线条加起来, 不就得到, 第 a_i 个输出节点的值了呀.
设 Softmax 的输出向量为 o \(= (o_1, o_2, o_3, ...o_k) ^T, 其中, o_j = \frac {e^{a_j}}{\sum \limits_k e^{a_k}}\) (归一化, 非常直观, 部分 / 部分总和嘛)
设 真实值的标签值为 t \(=(0, 1, 0, 1, 0, 0...)^T\) 假设这里是一个分类问题.
则误差函数为 \(L = \frac {1}{2} \sum \limits_k(o_k - t_k)^2\)
所有的求导都是偏导哈, 然后注意变量的这种链式关系(如上图): a -> o -> t , 分别是 n:1, 1: 1的关系
\(\nabla a_i = \frac {\partial _{0.5 \sum_k (o_k-t_k)^2}}{\partial a_i}\)
有中间变量 o, 即利用求导的链式法则 dt/da = dt/do * do/ da (上过高中就应该能掌握)
\(= \sum_k \frac {\partial (o_k-t_k)}{o_k} \frac {d\ o_k}{d\ a_i}\)
逐个击破, 先整 $\frac {d o_k}{d a_i} $
根据 Softmax 的定义, \(o_j = o_j = \frac {e^{a_j}}{\sum \limits_k e^{a_k}}\)
\(\frac {d\ o_j}{d\ a_i}= \frac {d\ \frac {e^{a_j}}{\sum \limits_k e^{a_k}}}{d\ a_i}\) 这里 a_j 是属于 k...K 的一个值.
当 i = j 的时候, 也就是 ai-> oi 就是图中输出层那里的 一 一 对应关系,
tips: 应用高数学的 分式 求导法则, 及大一学的 求偏导时, 将与之无关变量看作 常数
\(=\frac{e^{a_j} \sum_k e^{a_k} -e^{a_j} e^{ai} } {(\sum \limits_k e^{a_k})^2}\) 虽然是有求和, 但只有 i = j 的时候, 求导才对该变量有效, 取其余之是无关的.
\(=\frac{e^{a_j} ({\sum_k e^{a_k}} - e^{ai}) } {(\sum \limits_k e^{a_k})^2}\)
\(=\frac{e^{a_j}} {\sum \limits_k e^{a_k}} \ \frac{\sum _k e^{a_k}-e^{a_i}} {\sum \limits_k e^{a_k}}\)
\(=o_j (1-o_j).....(1)\)
当 i 与 j 不相等时, 跟上面一样的求导, 不同在于有很多无关项, 跟求导变量无关, 因此为0
\(\frac {d\ o_j}{d\ a_i}= \frac {d\ \frac {e^{a_j}}{\sum \limits_k e^{a_k}}}{d\ a_i}\)
\(=\frac{0 -e^{a_j} e^{ai} } {(\sum \limits_k e^{a_k})^2}\)
\(=\frac{-e^{a_j}} {\sum \limits_k e^{a_k}} \ \frac{e^{a_i}} {\sum \limits_k e^{a_k}}\)
\(=-o_j o_i .........(2)\)
因此,
\(\nabla a_i = \sum_k \frac {\partial (o_k-t_k)}{o_k} \frac {d\ o_k}{d\ a_i} = \sum \limits _k(o_k -t_k) [o_k (1_{ki}-o_i)]\)
继续
一定要记住变量代表啥哦, ai 就是 softmaxt 的输入啦, 也就是 最上面图中的 b_k 呀, 名字变了正常, 习惯嘛, 本质没变的
由 \(a_i = \sum \limits_j Wji \ h_j + b_i\)
\(\frac {\partial a_i}{\partial w_{pq}} = \sum\limits_j h_j \ \frac {\partial Wji}{Wpq} = \sum\limits_j h_j \ 1_{jp} \ 1_{iq} = h_p 1_{lq}\)
因此
\(\frac {\partial L}{\partial Wpq} = \sum \limits_i \frac{\partial L}{\partial a_i} \frac {\partial a_i}{\partial pq}\)
\(=\sum\limits_i \sum\limits_k (o_k - t_k) [o_k(1_{ki} -o_i)] * h_p 1_{lq}\)
小结
其实推导的过程, 就是 多元函数求偏导, 利用链式法则.
只要弄清楚, 输入层 -> 隐含层 -> 输出层 这个顺序所对应的 中间变量, 即明确目标是**对 权重值 Wij 来调整. 然后围绕这个权重相关的变量, 进行链式求导就好了呀, 其实真的不难的. 唯一可能比较难整的, 是变量的下标. 怎么理解呢, 只能在脑海里补充呀, 哪些是相关的, 无关, 变化的是什么这些. 只能自己去花时间领悟了呀, 一旦把一个问题, 从根源上去认识, 那, 真的就具备了看更宽阔天地的能力, 继续修炼, 真理来自内心的.