0. 前言
上篇博客对BP算法的大致步骤进行了总结,本篇博客将通过一个具体的例子来模拟一下这个算法的实现过程 !
1. BP算法例子说明
1.1 网络结构
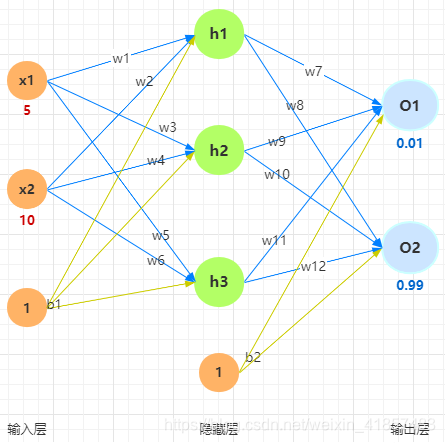
1.2 权重及偏移
w = ( 0.1 , 0.15 , 0.2 , 0.25 , 0.3 , 0.35 , 0.4 , 0.45 , 0.5 , 0.55 , 0.6 , 0.65 ) w=(0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65) w=(0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.65) 分别对应 w 1 w_1 w1 至 w 12 w_{12} w12
b = ( 0.35 , 0.65 ) b=(0.35, 0.65) b=(0.35,0.65) 对应 b 1 b_1 b1 和 b 2 b_2 b2
1.3 激活函数
Sigmoid函数: s i g m o i d ( x ) = sigmoid(x)= sigmoid(x)= 1 1 + e − x {1}\over{1+e^{-x}} 1+e−x1
1.4 正向传播
输入层到隐藏层
- h 1 h_1 h1 的线性计算结果以及经过激活函数计算后的结果
n e t h 1 = w 1 ⋅ x 1 + w 2 ⋅ x 2 + b 1 ⋅ 1 net_{h_1}=w_1\cdot x_1 + w_2\cdot x_2 +b_1\cdot1 neth1=w1⋅x1+w2⋅x2+b1⋅1
= 0.1 ⋅ 5 + 0.15 ⋅ 10 + 0.35 ⋅ 1 =0.1\cdot5+0.15\cdot10+0.35\cdot1 =0.1⋅5+0.15⋅10+0.35⋅1
= 2.35 =2.35 =2.35
o u t h 1 = 1 1 + e − n e t h 1 = 1 1 + e − 2.35 = 0.9129342275597286 ≈ 0.912934 out_{h_1}=\frac{1}{1+e^{-net_{h_1}}}=\frac{1}{1+e^{-2.35}}=0.9129342275597286\approx0.912934 outh1=1+e−neth11=1+e−2.351=0.9129342275597286≈0.912934
同上,计算 h 2 h_2 h2 和 h 3 h_3 h3
- h 2 h_2 h2 的线性计算结果以及经过激活函数计算后的结果
n e t h 2 = w 3 ⋅ x 1 + w 4 ⋅ x 2 + b 1 ⋅ 1 net_{h_2}=w_3\cdot x_1 + w_4\cdot x_2 +b_1\cdot1 neth2=w3⋅x1+w4⋅x2+b1⋅1
= 0.2 ⋅ 5 + 0.25 ⋅ 10 + 0.35 ⋅ 1 =0.2\cdot5+0.25\cdot10+0.35\cdot1 =0.2⋅5+0.25⋅10+0.35⋅1
= 3.85 =3.85 =3.85
o u t h 2 = 1 1 + e − n e t h 2 = 1 1 + e − 3.85 = 0.9791636554813196 ≈ 0.979164 out_{h_2}=\frac{1}{1+e^{-net_{h_2}}}=\frac{1}{1+e^{-3.85}}=0.9791636554813196\approx0.979164 outh2=1+e−neth21=1+e−3.851=0.9791636554813196≈0.979164 - h 3 h_3 h3 的线性计算结果以及经过激活函数计算后的结果
n e t h 3 = w 5 ⋅ x 1 + w 6 ⋅ x 2 + b 1 ⋅ 1 net_{h_3}=w_5\cdot x_1 + w_6\cdot x_2 +b_1\cdot1 neth3=w5⋅x1+w6⋅x2+b1⋅1
= 0.3 ⋅ 5 + 0.35 ⋅ 10 + 0.35 ⋅ 1 =0.3\cdot5+0.35\cdot10+0.35\cdot1 =0.3⋅5+0.35⋅10+0.35⋅1
= 5.35 =5.35 =5.35
o u t h 3 = 1 1 + e − n e t h 3 = 1 1 + e − 5.35 = 0.9952742873976046 ≈ 0.995274 out_{h_3}=\frac{1}{1+e^{-net_{h_3}}}=\frac{1}{1+e^{-5.35}}=0.9952742873976046\approx0.995274 outh3=1+e−neth31=1+e−5.351=0.9952742873976046≈0.995274
隐藏层到输出层
接下来需要计算 o 1 o_1 o1 和 o 2 o_2 o2 ,对于输出层计算,其输入就是上一层的输出,即 o u t h 1 out_{h_1} outh1、 o u t h 2 out_{h_2} outh2、 o u t h 3 out_{h_3} outh3,所以有如下计算过程:
-
o 1 o_1 o1 的线性计算结果以及经过激活函数计算后的结果
n e t o 1 = w 7 ⋅ o u t h 1 + w 9 ⋅ o u t h 2 + w 11 ⋅ o u t h 3 + b 2 ⋅ 1 net_{o_1}=w_7\cdot out_{h_1} + w_9\cdot out_{h_2} +w_{11}\cdot out_{h_3}+b_2\cdot1 neto1=w7⋅outh1+w9⋅outh2+w11⋅outh3+b2⋅1
= 0.4 ⋅ 0.912934 + 0.5 ⋅ 0.979164 + 0.6 ⋅ 0.995274 + 0.65 ⋅ 1 =0.4\cdot0.912934+0.5\cdot0.979164+0.6\cdot0.995274+0.65\cdot1 =0.4⋅0.912934+0.5⋅0.979164+0.6⋅0.995274+0.65⋅1
= 2.10192 =2.10192 =2.10192
o u t o 1 = 1 1 + e − n e t o 1 = 1 1 + e − 2.10192 = 0.8910896526253574 ≈ 0.891090 out_{o_1}=\frac{1}{1+e^{-net_{o_1}}}=\frac{1}{1+e^{-2.10192}}=0.8910896526253574\approx0.891090 outo1=1+e−neto11=1+e−2.101921=0.8910896526253574≈0.891090 -
o 2 o_2 o2 的线性计算结果以及经过激活函数计算后的结果
n e t o 2 = w 8 ⋅ o u t h 1 + w 10 ⋅ o u t h 2 + w 12 ⋅ o u t h 3 + b 2 ⋅ 1 net_{o_2}=w_8\cdot out_{h_1} + w_{10}\cdot out_{h_2} +w_{12}\cdot out_{h_3}+b_2\cdot1 neto2=w8⋅outh1+w10⋅outh2+w12⋅outh3+b2⋅1
= 0.45 ⋅ 0.912934 + 0.55 ⋅ 0.979164 + 0.65 ⋅ 0.995274 + 0.65 ⋅ 1 =0.45\cdot0.912934+0.55\cdot0.979164+0.65\cdot0.995274+0.65\cdot1 =0.45⋅0.912934+0.55⋅0.979164+0.65⋅0.995274+0.65⋅1
= 2.2462886 =2.2462886 =2.2462886
o u t o 2 = 1 1 + e − n e t o 2 = 1 1 + e − 2.2462886 = 0.9043299162220731 ≈ 0.904330 out_{o_2}=\frac{1}{1+e^{-net_{o_2}}}=\frac{1}{1+e^{-2.2462886}}=0.9043299162220731\approx0.904330 outo2=1+e−neto21=1+e−2.24628861=0.9043299162220731≈0.904330
误差
E t o t a l = E o 1 + E o 2 = 1 2 ( 0.01 − 0.891090 ) 2 + 1 2 ( 0.99 − 0.904330 ) 2 = 0.39182946850000006 ≈ 0.391829 E_{total}=E_{o_1}+E_{o_2}=\frac{1}{2}(0.01-0.891090)^{2}+\frac{1}{2}(0.99-0.904330)^{2}=0.39182946850000006\approx0.391829 Etotal=Eo1+Eo2=21(0.01−0.891090)2+21(0.99−0.904330)2=0.39182946850000006≈0.391829
1.5 反向传播
输入层和隐藏层之间
此处,以更新 w 7 w_7 w7 为例,要对其求偏导:
根据链式求导法则有:
∂ E t o t a l ∂ w 7 = ∂ E t o t a l ∂ o u t o 1 ⋅ ∂ o u t o 1 ∂ n e t o 1 ⋅ ∂ n e t o 1 ∂ w 7 \frac{\partial E_{total}}{\partial w_{7}}=\frac{\partial E_{total}}{\partial out_{o_1}}\cdot\frac{\partial out_{o_1}}{\partial net_{o_1}}\cdot\frac{\partial net_{o_1}}{\partial w_{7}} ∂w7∂Etotal=∂outo1∂Etotal⋅∂neto1∂outo1⋅∂w7∂neto1
这是因为 w 7 w_7 w7 的变化,会影响 n e t o 1 net_{o_1} neto1, n e t o 1 net_{o_1} neto1 又会影响 o u t o 1 out_{o_1} outo1, o u t o 1 out_{o_1} outo1 又会影响 E o 1 E_{o_1} Eo1,最终影响 E t o t a l E_{total} Etotal
即, w 7 → n e t o 1 → o u t o 1 → E o 1 → E t o t a l w_7\rightarrow net_{o_1}\rightarrow out_{o_1}\rightarrow E_{o_1}\rightarrow E_{total} w7→neto1→outo1→Eo1→Etotal
PS:
上面的过程其实就类似于对一个复合函数求偏导,假设对复合函数 f ( g ( h ( x ) ) ) f(g(h(x))) f(g(h(x))) 求偏导,就是: ∂ f ∂ x = ∂ f ∂ g ⋅ ∂ g ∂ h ⋅ ∂ h ∂ x \frac{\partial f}{\partial x}=\frac{\partial f}{\partial g}\cdot\frac{\partial g}{\partial h}\cdot\frac{\partial h}{\partial x} ∂x∂f=∂g∂f⋅∂h∂g⋅∂x∂h
又,
E o 1 = 1 2 ( r e a l o 1 − o u t o 1 ) 2 E_{o_1}=\frac{1}{2}(real_{o_1}-out_{o_1})^2 Eo1=21(realo1−outo1)2
E t o t a l = E o 1 + E o 2 E_{total}=E_{o_1}+E_{o_2} Etotal=Eo1+Eo2
所以,
∂ E t o t a l ∂ o u t o 1 = 2 ⋅ 1 2 ( r e a l o 1 − o u t o 1 ) ⋅ ( − 1 ) + 0 = − ( 0.01 − 0.891090 ) = 0.88109 \frac{\partial E_{total}}{\partial out_{o_1}}=2\cdot\frac{1}{2}(real_{o_1}-out_{o_1})\cdot(-1)+0=-(0.01-0.891090)=0.88109 ∂outo1∂Etotal=2⋅21(realo1−outo1)⋅(−1)+0=−(0.01−0.891090)=0.88109
又,
o u t o 1 = 1 1 + e − n e t o 1 out_{o_1}=\frac{1}{1+e^{-net_{o_1}}} outo1=1+e−neto11
所以,
∂ o u t o 1 ∂ n e t o 1 = o u t o 1 ⋅ ( 1 − o u t o 1 ) = 0.891090 ⋅ ( 1 − 0.891090 ) = 0.09704861189999996 ≈ 0.097049 \frac{\partial out_{o_1}}{\partial net_{o_1}}=out_{o_1}\cdot(1-out_{o_1})=0.891090\cdot(1-0.891090)=0.09704861189999996\approx0.097049 ∂neto1∂outo1=outo1⋅(1−outo1)=0.891090⋅(1−0.891090)=0.09704861189999996≈0.097049
PS:
这一步的偏导,其实就是对sigmoid函数求导数:
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
g ′ ( z ) = e − z ( 1 + e − z ) 2 = 1 + e − z − 1 ( 1 + e − z ) 2 = 1 ( 1 + e − z ) − 1 ( 1 + e − z ) 2 = g ( z ) ⋅ ( 1 − g ( z ) ) g'(z)=\frac{e^{-z}}{(1+e^{-z})^2}=\frac{1+e^{-z}-1}{(1+e^{-z})^2}=\frac{1}{(1+e^{-z})}-\frac{1}{(1+e^{-z})^2}=g(z)\cdot(1-g(z)) g′(z)=(1+e−z)2e−z=(1+e−z)21+e−z−1=(1+e−z)1−(1+e−z)21=g(z)⋅(1−g(z))
又,
n e t o 1 = w 7 ⋅ o u t h 1 + w 9 ⋅ o u t h 2 + w 11 ⋅ o u t h 3 + b 2 ⋅ 1 net_{o_1}=w_7\cdot out_{h_1} + w_9\cdot out_{h_2} +w_{11}\cdot out_{h_3}+b_2\cdot1 neto1=w7⋅outh1+w9⋅outh2+w11⋅outh3+b2⋅1
所以,
∂ n e t o 1 ∂ w 7 = o u t h 1 + 0 + 0 + 0 = 0.912934 \frac{\partial net_{o_1}}{\partial w_{7}}=out_{h_1}+0+0+0=0.912934 ∂w7∂neto1=outh1+0+0+0=0.912934
故,
∂ E t o t a l ∂ w 7 = ∂ E t o t a l ∂ o u t o 1 ⋅ ∂ o u t o 1 ∂ n e t o 1 ⋅ ∂ n e t o 1 ∂ w 7 = 0.88109 ⋅ 0.097049 ⋅ 0.912934 ≈ 0.078064 \frac{\partial E_{total}}{\partial w_{7}}=\frac{\partial E_{total}}{\partial out_{o_1}}\cdot\frac{\partial out_{o_1}}{\partial net_{o_1}}\cdot\frac{\partial net_{o_1}}{\partial w_{7}}=0.88109\cdot0.097049\cdot0.912934\approx0.078064 ∂w7∂Etotal=∂outo1∂Etotal⋅∂neto1∂outo1⋅∂w7∂neto1=0.88109⋅0.097049⋅0.912934≈0.078064
再根据梯度下降的原理,对 w 7 w_7 w7 进行更新:
w 7 ′ = w 7 − α ∂ E t o t a l ∂ w 7 = 0.4 − 0.5 ⋅ 0.078064 = 0.360968 w_7'=w_7-\alpha \frac{\partial E_{total}}{\partial w_{7}}=0.4-0.5\cdot0.078064=0.360968 w7′=w7−α∂w7∂Etotal=0.4−0.5⋅0.078064=0.360968
上面的 α \alpha α 是学习率,是可以人为设定的,具体的梯度下降的原理介绍可以参见这篇博客;
上面整个反向传播是以调整 w 7 w_7 w7 的值为例,对于其他的 w w w 的更新也是与上述过程类似的 !
所以,同理得到下面的更新:
w 8 ′ = 0.453383 w'_8=0.453383 w8′=0.453383, w 9 ′ = 0.458137 w'_9=0.458137 w9′=0.458137, w 10 ′ = 0.553629 w'_{10}=0.553629 w10′=0.553629, w 11 ′ = 0.557448 w'_{11}=0.557448 w11′=0.557448, w 12 ′ = 0.653688 w'_{12}=0.653688 w12′=0.653688
观察这一层 w w w 的变化,可以看到 w 7 , 9 , 11 w_{7,9,11} w7,9,11 在原来的基础上都减小了;而 w 8 , 10 , 12 w_{8,10,12} w8,10,12 在原来的基础上都增大了,这个变化也正好符合真实值的结果。
隐藏层和输入层之间
此处,以更新 w 1 w_1 w1 为例:
w 1 → n e t h 1 → o u t h 1 → n e t o 1 → o u t o 1 → E o 1 → E t o t a l w_1\rightarrow net_{h_1}\rightarrow out_{h_1}\rightarrow net_{o_1}\rightarrow out_{o_1}\rightarrow E_{o_1}\rightarrow E_{total} w1→neth1→outh1→neto1→outo1→Eo1→Etotal
w 1 → n e t h 1 → o u t h 1 → n e t o 2 → o u t o 2 → E o 2 → E t o t a l w_1\rightarrow net_{h_1}\rightarrow out_{h_1}\rightarrow net_{o_2}\rightarrow out_{o_2}\rightarrow E_{o_2}\rightarrow E_{total} w1→neth1→outh1→neto2→outo2→Eo2→Etotal
此处对其求偏导稍微复杂一点:
∂ E t o t a l ∂ w 1 = ∂ E t o t a l ∂ o u t h 1 ⋅ ∂ o u t h 1 ∂ n e t h 1 ⋅ ∂ n e t h 1 ∂ w 1 = ( ∂ E o 1 ∂ o u t h 1 + ∂ E o 2 ∂ o u t h 1 ) ⋅ ∂ o u t h 1 ∂ n e t h 1 ⋅ ∂ n e t h 1 ∂ w 1 \frac{\partial E_{total}}{\partial w_{1}}=\frac{\partial E_{total}}{\partial out_{h_1}}\cdot\frac{\partial out_{h_1}}{\partial net_{h_1}}\cdot\frac{\partial net_{h_1}}{\partial w_{1}}=(\frac{\partial E_{o_1}}{\partial out_{h_1}}+\frac{\partial E_{o_2}}{\partial out_{h_1}})\cdot\frac{\partial out_{h_1}}{\partial net_{h_1}}\cdot\frac{\partial net_{h_1}}{\partial w_{1}} ∂w1∂Etotal=∂outh1∂Etotal⋅∂neth1∂outh1⋅∂w1∂neth1=(∂outh1∂Eo1+∂outh1∂Eo2)⋅∂neth1∂outh1⋅∂w1∂neth1
∂ E o 1 ∂ o u t h 1 = ∂ E o 1 ∂ o u t o 1 ⋅ ∂ o u t o 1 ∂ n e t o 1 ⋅ ∂ n e t o 1 ∂ o u t h 1 \frac{\partial E_{o_1}}{\partial out_{h_1}}=\frac{\partial E_{o_1}}{\partial out_{o_1}}\cdot\frac{\partial {out_{o_1}}}{\partial net_{o_1}}\cdot\frac{\partial {net_{o_1}}}{\partial out_{h_1}} ∂outh1∂Eo1=∂outo1∂Eo1⋅∂neto1∂outo1⋅∂outh1∂neto1
后面的计算与更新过程与上边类似 !
上面的整个更新就算是一次的更新,随着迭代次数的增加,会越来越接近真实的结果。
以上就是整个FP及BP过程的举例说明,下面将用代码来模拟一下这个过程 !