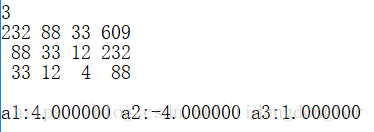hdu 6198 number number number

题目链接

题目给定斐波那契数列递推公式F(n)，要找出不满足k个F(i)（0<=i<=k）之和等于任意整数的n值是多少。

先暴力打表：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1000;

ll f[N];
ll ans[200][2000];

int main(){
	f[0]=0;
	f[1]=1;
	f[2]=1;
	
	for(int i=2;i<=1000;i++){
		f[i]=f[i-1]+f[i-2];
		
	}
	
	for(int i=0;i<=15;i++){
		printf("f[%d]=%lld\n",i,f[i]);
	}
		
	memset(ans,0,sizeof(ans));
	ans[0][0]=1;
	
	for(int i=0;i<=40;i++){
		for(int k=1;k<=40;k++){
			for(int j=f[i];j<1000;j++)
				ans[k][j]+=ans[k-1][j-f[i]];
		}
	}
	
	for(int i=0;i<=40;i++){
		for(int j=1;j<=700;j++)
			if(ans[i][j]==0){
				printf("%d\n",j);
				break;
			} 
				
	}
	
	return 0;
}

   一直尝试发现递推式有三项：

   

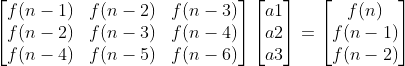
利用高斯消元法得出：

所以得出公式 f(n)=4f(n-1)-4f(n-2)+f(n-3);  再利用矩阵快速幂求解f(n)即可

     f(1)=4, f(2)=12, f(3)=33

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const ll mod=998244353;
struct matrix{
	ll x[3][3];
};
matrix multi(matrix a,matrix b)//矩阵相乘
{
	matrix temp;
	memset(temp.x,0,sizeof(temp.x));
	for(int i=0;i<3;i++)
		for(int j=0;j<3;j++)
			for(int k=0;k<3;k++)
			{
				temp.x[i][j]+=a.x[i][k]*b.x[k][j];
				temp.x[i][j]%=mod;//负数取模的问题,除法取模
			}
	return temp;
}
matrix quick_multi(matrix a,ll n)//矩阵快速幂
{
	matrix temp=a;
	n--;
	while(n){
		if(n&1)
			temp=multi(temp,a);
		a=multi(a,a);
		n>>=1;
	}
	return temp;
}
int main()
{
	ll n;
	while(cin>>n)
	{
		if(n==1)
		{
			printf("4\n");
			continue;
		}
		if(n==2)
		{
			printf("12\n");
			continue;
		}
		if(n==3)
		{
			printf("33\n");
			continue;
		}

		matrix A;
		matrix ans;
		memset(A.x,0,sizeof(A.x));
		memset(ans.x,0,sizeof(ans.x));
		A.x[0][0]=4;A.x[1][0]=-4;A.x[2][0]=1;
		A.x[0][1]=1;A.x[1][2]=1;A.x[2][2]=0;
		
		ans.x[0][0]=33,ans.x[0][1]=12,ans.x[0][2]=4;
		A=quick_multi(A,n-3);
		ans=multi(ans,A);
		printf("%lld\n",(ans.x[0][0]+mod)%mod);
	}

	return 0;
}