定义:
设G = (V, E)是连通的无向图,T是图G的一个最小生成树.如果有另外一棵树T1,T1 ≠ T,满足不存在树T',T' ≠ T,w(T') < w(T1),则称T1是图G的次小生成树.
算法:
1:基本算法
最简单也最容易想到的是,设T是G的最小生成树,依次枚举T的边并去掉,再求最小生成树,所得到的这些值的最小值就是次小生成树,由于最小生成树有N-1条边,这种方法就相当于运行了N次最小生成树的算法,算法的时间复杂度比较高.大约是N * M的数量级.
2:算法二
定义由最小生成树T进行一次可行变化得到的新的生成树所组成的集合,称为树T的邻集,记为N(T).所谓可行变化即去掉T中的一条边,再新加入G中的一条边,使得新生成的图仍为树.设T是图G的最小生成树,如果T1满足w(T1) = min{ w(T') | T' E N(T)},则T1是图G的次小生成树.
定理:如果图G的边的个数E和个点的个数N不满足关系E + 1 = N,那么存在边(u,v) 属于 T 和(x, y)不属于T满足T \ (u, v) U (x, y)是图的一颗次小生成树.
既然存在边(u, v) 属于 T 和(x, y) 不属于T满足T \ (u, v) U (x, y)是图的一颗次小生成树,那么所有的T \ (u, v) U (x, y)刚好构成了T的邻集,则T的邻集中权值最小的就是次小生成树了,但是如果每次枚举(u, v)和(x, y),还要判断能否构成一棵树,复杂度太高.那么这里应该这么做,先加入(x,y),对于一棵树加入(x, y)后一定会成环,如果删去环上除(x ,y)以外权值最大的一条边,会得到加入(x,y)时权值最小的边.那么接下来的问题就是如何快速求得这个环上权值最大边了.最小生成树中x到y的最长边可以使用树形动态规划或者LCA等方法在O(N2)的时间复杂度内计算出来.但是如果使用的是Kruskal算法求最小生成树,可以在算法的运行过程中求出x到y路径上的最长边,因为每次合并两个等价类的时候,分别属于两个等价类的每两个点之间的最长边一定是当前加入的边,按照这条性质进行记录的话就可以求出来最小生成树中在每两个点的路径上的最长边.
算法实现上,首先用求最小生成树的算法求出其权值之和为mst,然后枚举不属于最小生成树的边(x, y),并添加到最小生成树中,那么树必定形成环,然后删掉这个环内(不包含(x,y))最长的边.然后计算权值之和,枚举所有不属于最小生成树的边,取其权值的最小值,就是次小生成树.
下面用图来说明下计算(x,y)之间的最长边:
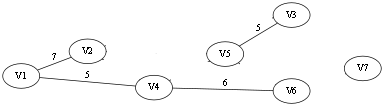
比如利用 kruskal 走到了上述步骤,接下来要添加边(V2, V5),已知权值为8,那么V2 和 V5 分别属于两个等价类<V2, V1, V4, V6> 和 <V5, V3> 的每两个点之间的距离应该都更新为8,即length[3][2] = length[3][1] = length[3][4] = length[3][6] = 8, length[5][2] = length[5][1] = length[5][4] = length[5][6] = 8,每增加一条边,就如此的更新下去,最后就可以得到图中两个节点之间的路径上的最长距离.
下面再用图简单阐述下算法:
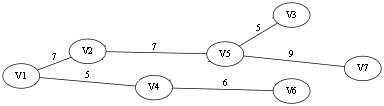
假设上图是图的最小生成树,并存在边(v5, v6),且其权值为8,那么当枚举到此条边时,在图中添加边(v5,v6),图中便有了一个环,在此环中找到除新加边以外最大的边的权值为7,那么删除此边,计算权值,然后继续枚举其他不存在于最小生成树的边,从中取得最小值,就是要求的答案.
Prim解法:
#include<cstdio>
#include<cstring>
#include<algorithm>
#define Inf 0x3f3f3f3f
using namespace std;
const int N = 1005;
int G[N][N],//存放原图
used[N][N],//记录i-j这条边是否在最小生成树上
path[N][N];//i-j之间最大的边长
int vis[N],dis[N],per[N];
int n,m;
void init(){
memset(used,0,sizeof(used));
memset(path,0,sizeof(path));
memset(G,Inf,sizeof(G));
}
int Prim(int s){
memset(vis,0,sizeof(vis));
int sum=0;
for(int i=1;i<=n;i++){
dis[i]=G[s][i];
per[i]=s;
}
vis[s]=1;
for(int i=1;i<n;i++){
int mint=Inf;
int u=s;
for(int j=1;j<=n;j++){
if(!vis[j]&&dis[j]<mint){
mint=dis[j];
u=j;
}
}
vis[u]=1;
sum+=mint;
used[u][per[u]]=used[per[u]][u]=1;
for(int j=1;j<=n;j++){
if(vis[j]&&j!=u) //j到u路径上的最大值
path[j][u]=path[u][j]=max(path[j][per[u]],dis[u]);
if(!vis[j]){
if(dis[j]>G[u][j]){
dis[j]=G[u][j];
per[j]=u;
}
}
}
}
return sum;
}
int SecPrim(int x){
printf("%d\n",x);
int ans=Inf;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i!=j&&!used[i][j]) //去掉i,j 之间的最大值,加上i-j这条边
ans=min(ans,x-path[i][j]+G[i][j]);
return ans;
}
int main(){
while(~scanf("%d%d",&n,&m)){
init();
for(int i=1;i<=m;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
G[u][v]=G[v][u]=w;
}
int temp=Prim(1);
int ans=SecPrim(temp);
printf("最小生成树: %d\n",temp)
printf("次小生成树: %d\n",ans);
}
return 0;
}