题目描述
On Mars, there is a huge company called ACM (A huge Company on Mars), and it’s owned by a younger boss.
Due to no moons around Mars, the employees can only get the salaries per-year. There are nemployees in ACM, and it’s time for them to get salaries from their boss. All employees are numbered from 1 to n. With the unknown reasons, if the employee’s work number is k, he can get k^4 Mars dollars this year. So the employees working for the ACM are very rich.
Because the number of employees is so large that the boss of ACM must distribute too much money, he wants to fire the people whose work number is co-prime with n next year. Now the boss wants to know how much he will save after the dismissal.
题目翻译(XJH版本)
又若干年之后,XJH成为了一个上市企业的老板,然而是一个抠门的老板(XJH:???)。
XJH的公司里面有n个员工,编号是1~n。每个人的工资是自己编号的四次方,例如,编号为5的员工,工资就是54=625。 (员工1:???)
然而,XJH觉得工资发的太多了,需要裁员。于是,决定把所有编号和自己互质的员工都裁掉(XJH的编号显然是n,肥水不流外人田)。 现在,问:XJH裁员之后能省多少钱?
解题思路
我们直接一上来就能看出一种O(n)的做法,那就是一个数一个数的枚举,如果这个数没有被访问过并且和n是互质的,那么这个数的次方都与n互质,计算的过程中顺便把vis标记一下,标准的O(n),标准的TLE。。。。
我们不妨转换一下思路:我们不妨求所有于所有与n不互质的数的四次方之和,再用 ∑n^4 把它减掉,也能得到所有的结果。并且,1e8以内的数的质因子个数很少,所以这样应该不会超时,但是还有一个难点——如何推出四次方求和公式?
我们退而求其次,不妨先求出更低次的求和公式:
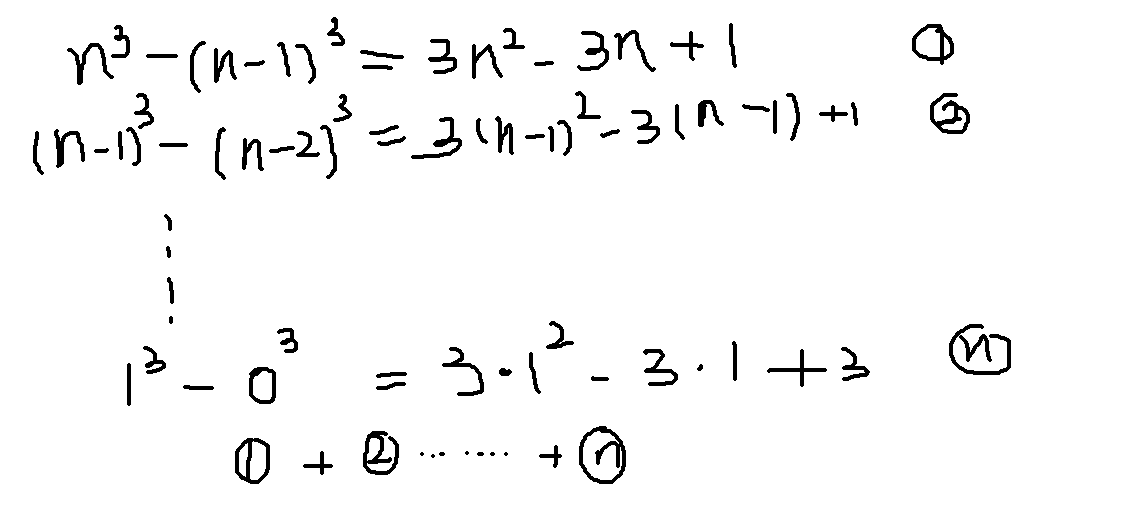
这样,我们就可以推出二次求和公式,以此类推,我们就可以得到4次求和公式:
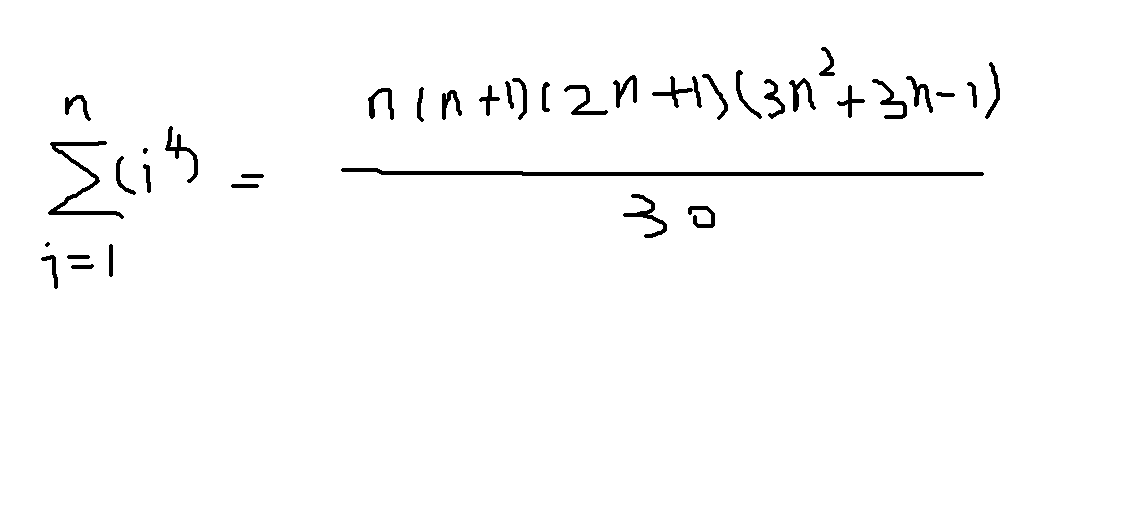
既然有除,又有膜,所以我们就要用到逆元了。
比如n与3不互质,那和6,9,12,15也就不互质,那么我们将这个数列除以3,就得到差为1的等差数列,这样我们就很容易求了。运用容斥原理,二进制枚举就可以了。
代码
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #define ll long long 6 using namespace std; 7 const int maxn=10050; 8 const ll MOD=1e9+7; 9 const ll ni=233333335; 10 bool pri[maxn]; 11 ll p[maxn],num[maxn]; 12 ll T,n,cnt=0,tot=0,ans; 13 inline void ini(){ 14 pri[1]=0; 15 for(register int i=2;i<maxn;i++){ 16 if(pri[i]){ 17 p[++cnt]=i; 18 for(register int j=2;j*i<maxn;j++)pri[i*j]=0; 19 } 20 } 21 } 22 inline ll ksm(ll a,ll b){ 23 ll c=1; 24 while(b){ 25 if(b&1)c=c*a%MOD; 26 a=a*a%MOD,b>>=1; 27 } 28 return c%MOD; 29 } 30 inline ll calc(ll x){ 31 ll y=x%MOD; 32 y=y*(x+1)%MOD; 33 y=y*(2*x+1)%MOD; 34 y=y*((3*x*x+3*x-1)%MOD)%MOD; 35 y=y*ni%MOD; 36 return y; 37 } 38 inline void resolve(ll x){ 39 for(register int i=1;i<=cnt;i++){ 40 if(p[i]>x)break; 41 if(x/p[i]*p[i]==x){ 42 num[++tot]=p[i]; 43 while(x/p[i]*p[i]==x)x/=p[i]; 44 } 45 } 46 if(x>1)num[++tot]=x; 47 } 48 int main(){ 49 memset(pri,1,sizeof(pri)); 50 ini(); 51 scanf("%lld",&T); 52 while(T--){ 53 memset(num,0,sizeof(num)); 54 tot=ans=0; 55 scanf("%lld",&n); 56 ans=calc(n); 57 resolve(n); 58 for(register ll i=1;i<(1<<tot);i++){ 59 ll tmp=1,cnt1=0; 60 for(register ll j=0;j<tot;j++){ 61 if(i&(1<<j)){ 62 cnt1++; 63 tmp=tmp*num[j+1]%MOD; 64 } 65 } 66 // 67 if(cnt1&1){ 68 ans=(ans-(calc(n/tmp)*ksm(tmp,4))%MOD+MOD)%MOD; 69 } 70 else { 71 ans=(ans+(calc(n/tmp)*ksm(tmp,4))%MOD+MOD)%MOD; 72 } 73 } 74 printf("%lld\n",(ans+MOD)%MOD); 75 } 76 }