动态规划详解（第三讲)——矩阵链相乘

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/Neo_kh/article/details/81282025

这类题目体现了DP的实质，也是经典问题。(•̀˓◞•́)

假设我们要用标准的矩阵乘法计算$M_1$、$M_2$、$M_3$的乘积$M_1M_2M_3$，这三个矩阵的维数分别是2x10，10x2，2x10。

• 如果我们先把$M_1$和$M_2$相乘，然后把结果和$M_3$相乘，即$（（M_1M_2）M_3）$。那么要进行2x10x2+2x2x10=80次乘法；
• 如果我们先乘$M_2$$M_3$，结果再与$M_1$相乘，即$（M_1（M_2M_3））$。那么数量乘法的次数就变成了：10x2x10+2x10x10=400。

可见，矩阵链相乘时的顺序不同，运算量也不同。而我们的目的是找到一种乘法顺序使得运算量最小。

---

递推关系式

我们注意到，对于矩阵链$M_1M_2...M_i$，矩阵$M_i$的列数一定等于矩阵$M_{i+1}$的行数（$1\le i<n$），这是由矩阵乘法的定义决定的。
因此，对于一个矩阵链，我们指定每个矩阵的行数和最右面矩阵$M_n$的列数就可以了。假设有n+1维数$r_1,r_2,...,r_{n+1}$,这里$r_i$表示矩阵$M_i$的行数（$1\le i\le n$），$r_{n+1}$表示最矩阵$M_n$的列数。
以后，我们用$M_{i,j}$来记$M_iM_{i+1}...M_j$的乘积。用$C[i][j]$来记录链$M_{i,j}$数量乘法的次数。
对于给定的一对索引$i$和$j，1\le i<j<\le n$，$M_{i,j}$可用如下方法计算：

• 设$k$是$i+1$和$j$之间的一个索引，索引$k$把矩阵链$M_{i,j}$分成了两部分：$M_{i,k-1}=M_iM_{i+1}...M_{k-1}$和$M_{k,j}=M_kM_{k+1}...M_j$。所以$M_{i,j}=M_{i,k-1}M_{k,j}$。

  用这种方法计算$M_{i,j}$的耗费（即数量乘法的次数），是计算$M_{i,k-1}$的耗费加上计算$M_{k,j}$的耗费再加上$M_{i,k-1}$乘以$M_{k,j}$的耗费（它是$r_ir_kr_{j+1}$）。

  我们需要遍历$k$，找到使乘法$M_iM_{i+1}...M_j$所需的数量乘法最小的$k$值，我们有以下递推式：
  $C[i][j]=$$Min\over i<k\le j$$\{C[i][k-1]+C[k][j]+r_ir_kr_{j+1}\}$
  为了找出$M_1M_2..M_n$的乘法次数，我们只需要解递推式：
  $C[1][n]=$$Min\over 1<k\le n$$\{C[1][k-1]+C[k][n]+r_ir_kr_{n+1}\}$

填表

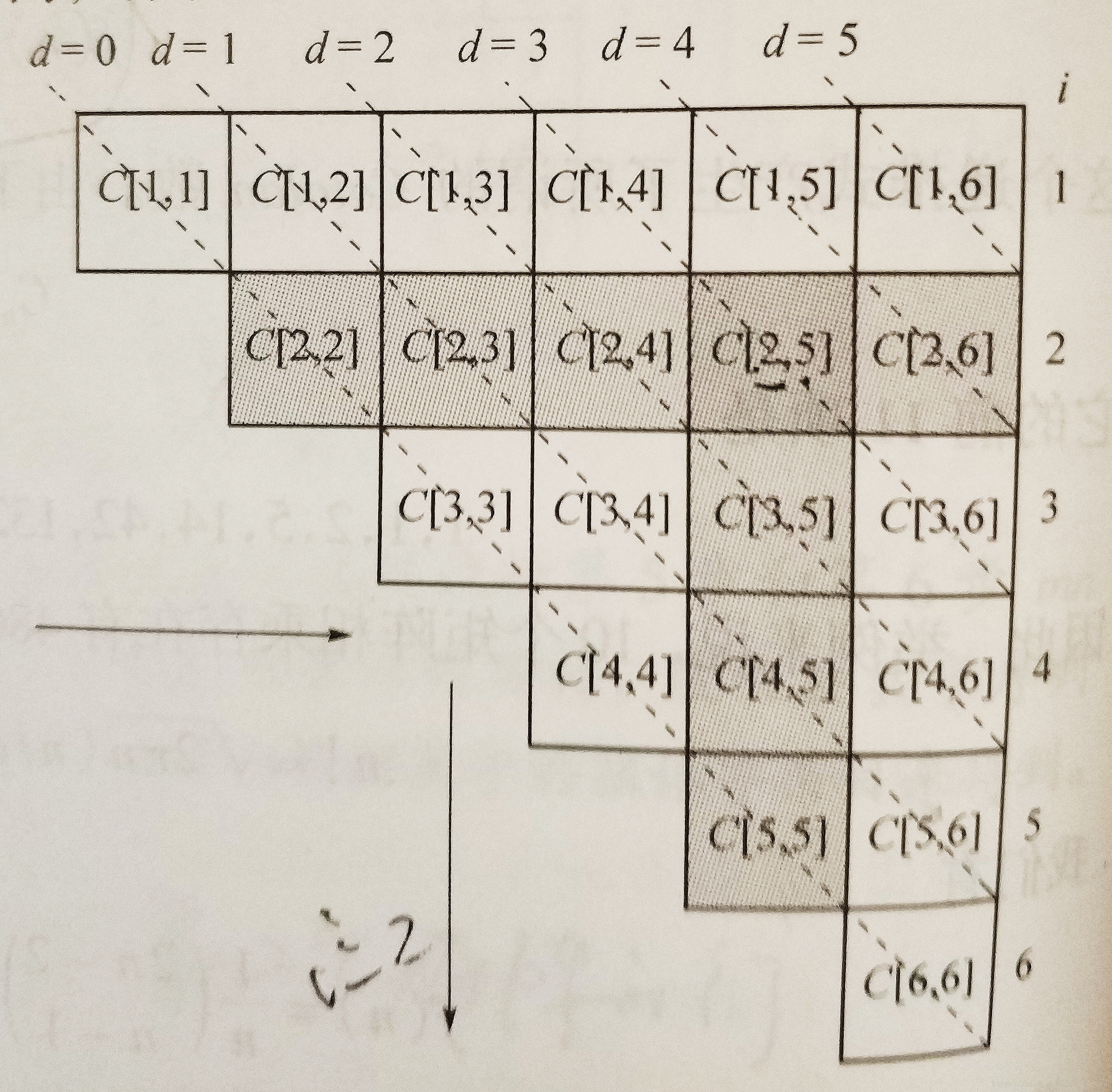
假设我们要求$n=6$个矩阵相乘。考虑下图：

对角线$d$用乘出各种$d+1$个相继矩阵的最小耗费填满。特别地，对角线5恰好由一项组成，它表示6个矩阵相乘的最小耗费，这就是我们要求的结果。
我们从对角线0开始，到对角线5为止，沿着对角线填充这个三角形表。

• 首先在对角线0中，每个链仅由一个矩阵的组成，没有数量乘法，因此这个对角线填0。
• 接着，对角线1由两个连续的矩阵相乘的耗费来填充。如C[2][3]用$M_2M_3$的乘法耗费来填。
• 余下的对角线根据上面的递推式和先前存储在表中值来填。举例来说，C[2][5]的值为以下三个耗费的最小值：
  – (1)计算$M_{2,2}$的耗费（即C[2][2])加上计算$M_{3,5}$（即C[3][5]）的耗费，再加上$M_{2,2}$乘以$M_{3,5}$的耗费。
  – (2)计算$M_{2,3}$的耗费（即C[2][3])加上计算$M_{4,5}$（即C[4][5]）的耗费，再加上$M_{2,3}$乘以$M_{4,5}$的耗费。
  – (3)计算$M_{2,4}$的耗费（即C[2][4])加上计算$M_{5,5}$（即C[5][5]）的耗费，再加上$M_{2,4}$乘以$M_{5,5}$的耗费。

---

伪代码

下面我们给出算法的伪代码实现
MATCHAIN
输入：n个矩阵的链的维数对应于正整数数组$r[1...n+1]$，其中，$r[1...n]$是n个矩阵的行数，$r[n+1]$是$M_n$的列数。
输出：n个矩阵相乘的数量乘法的最小次数。

for i=1 to n {填充对角线d0}
    C[i,i]=0;
end for
for d=1 to n-1 {填充对角线d1到dn-1}
    for i=1 to n-d {填充对角线di的项目}
        j=i+d
        comment:下列三行计算C[i,j]
        C[i,j]=inf
        for k=i+1 to j
            C[i,j]=Min{C[i,j],C[i,k-1]+C[k,j]+r[i]*r[k]*[j+1]
        end for
    end for
end for
return C[1,n]

时空复杂度

对于某个常数c>0，算法的运行时间正比于:

$$\sum_{d=1}^{n-1} \sum_{i=1}^{n-d} \sum_{k=1}^{d} c = \frac{cn^3-cn}{6}$$
因此算法的时间复杂度是 $\Theta(n^3)$

显然，算法所需要的内存空间取决于所需要的三角数组的大小，也就是$\Theta(n^2）$。