FFT快速傅里叶转换

转载自

FFT——快速傅里叶变换

这块不写东西空荡荡的，我决定还是把FFT的定义给贴上吧

FFT（Fast Fourier Transformation）是离散傅氏变换（DFT）的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。

这三段话其实一点用也没有

FFT是干什么的

FFT在算法竞赛中就有一个用途：加速多项式乘法(暴言)

简单来说，形如 a0X0+a1X1+a2X2+⋯+anXna0X0+a1X1+a2X2+⋯+anXn 的代数表达式叫做多项式，可以记作f(X)=a0X0+a1X1+a2X2+⋯+anXnf(X)=a0X0+a1X1+a2X2+⋯+anXn ，其中a0,a1,⋯,ana0,a1,⋯,an 叫做多项式的系数，XX 是一个不定元(就是不可以合并)，不表示任何值，不定元在多项式中最大项的次数称作多项式的次数

如果我们当前有两个多项式f(X),g(X)f(X),g(X) ，现在要把他们乘起来(求卷积)，最朴素的做法就是

∑i=02n−1(∑j=0iai∗bi−j)∗xi∑i=02n−1(∑j=0iai∗bi−j)∗xi

这样的复杂度是Θ(n2)Θ(n2) 的，十分不美观，FFT就是要将这个过程优化为Θ(nlogn)Θ(nlog⁡n)

前置技能

多项式

见上文

复数

复数形如a+bia+bi ，其中i=−1−−−√i=−1

aa 叫作复数的实部，bibi 叫做复数的虚部

复数(a1+b1i)∗(a2+b2i)(a1+b1i)∗(a2+b2i) 相乘的值，即a1a2−b1b2+(a1b2+a2b1)ia1a2−b1b2+(a1b2+a2b1)i 也是一个复数，同时我们也得到了复数的乘法法则

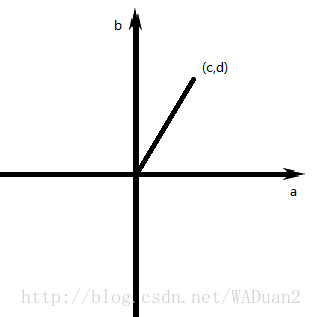
复数c+dic+di 可以用这种方式表示出来

复数乘法的在复平面中表现为辐角相加，模长相乘

单位根

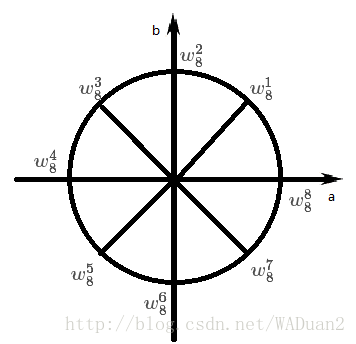
复数ww 满足wn=1wn=1 称作ww 是nn 次单位根，下图包含了所有的88 次单位根(图中圆的半径是1)

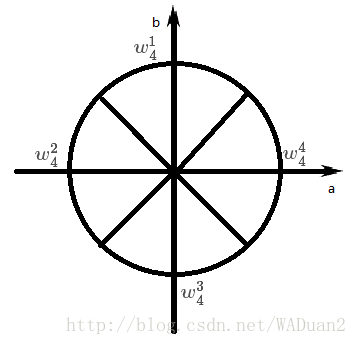
同样的，下图是所有的4次单位根

聪明的你也许已经发现了单位根的些许性质，即

w2m2n=wmnw2n2m=wnm

wmn=−wm+n2nwnm=−wnm+n2

这两个要记住，一会很有用

多项式的系数表达法

我们有多项式f(X)=a0X0+a1X1+a2X2+⋯+anXnf(X)=a0X0+a1X1+a2X2+⋯+anXn ，令a⃗=(a0,a1,a2,...,an)a→=(a0,a1,a2,...,an) ，则称A(X)A(X) 为多项式f(X)f(X) 的系数表示法

在系数表示法下，计算多项式乘法是Θ(n2)Θ(n2) 的

多项式的点值表达法

任取n+1n+1 个互不相同的S={p1,p2,...,pn+1}S={p1,p2,...,pn+1} ，对f(X)f(X) 分别求值得到f(p1),f(p2),...,f(pn+1)f(p1),f(p2),...,f(pn+1) ，那么称A(X)={(p1,f(p1)),(p2,f(p2)),...,(pn+1,f(pn+1))}A(X)={(p1,f(p1)),(p2,f(p2)),...,(pn+1,f(pn+1))} 为多项式f(X)f(X) 在SS 下的点值表示法

可以把多项式想象成一个nn 次函数，点值表示法就是取SS 下每一个横坐标时对应的点，因为nn 次函数可以由n+1n+1 个点确定下来(可以将每一个点列一个nn 次方程)，所以nn 维点值与nn 维系数一一对应

更重要的一点，点值表示法下的乘法运算获得了简化

两个多项式PP ,QQ 分别取点(x,y1)(x,y1) 和(x,y2)(x,y2) ，P∗QP∗Q 就会取到点(x,y1∗y2)(x,y1∗y2) ；

令C=P∗QC=P∗Q ，因为C(X)=P(X)∗Q(X)C(X)=P(X)∗Q(X) ，所以C(x)=P(x)∗Q(x)C(x)=P(x)∗Q(x) ，即C(x)=y1∗y2C(x)=y1∗y2

所以在点值表示法下，计算多项式乘法是Θ(n)Θ(n) 的

FFT的具体过程

FFT就是将系数表示法转化成点值表示法相乘，再由点值表示法转化为系数表示法的过程，第一个过程叫做求值(DFT)，第二个过程叫做插值(IDFT)

求值

还记得我们之前提到的单位根吗？再回顾一下：

w2m2n=wmnw2n2m=wnm

wmn=−wm+n2nwnm=−wnm+n2

想要求出一个多项式的点值表示法，需要选出n+1n+1 个数分别带入到多项式里面，带入一个数的复杂度是Θ(n)Θ(n) 的，那么总复杂度就是Θ(n2)Θ(n2) 的，因为单位根有上面两个优美的性质，所以我们尝试可以取nn 次单位根组成SS ，看看能不能加速我们的运算

设A0(X)A0(X) 为A(X)A(X) 偶次项的和，设A1(X)A1(X) 为A(X)A(X) 奇次项的和，即

A0(X)=a0x0+a2x1+...+an−1xn/2A0(X)=a0x0+a2x1+...+an−1xn/2

A1(X)=a1x0+a3x1+...+an−2xn/2A1(X)=a1x0+a3x1+...+an−2xn/2

因为A(wmn)=a0w0n+a1wmn+a2w2mn+a3w3mn+...+an−1w(n−1)∗mn+anwnmnA(wnm)=a0wn0+a1wnm+a2wn2m+a3wn3m+...+an−1wn(n−1)∗m+anwnnm

所以有

​ A(wmn)==A0((wmn)2)+wmnA1((wmn)2)A0(wmn2)+wmnA1(wmn2)A(wnm)=A0((wnm)2)+wnmA1((wnm)2)=A0(wn2m)+wnmA1(wn2m)

​ A(wm+n2n)==A0((wmn)2)+wm+n2nA1((wmn)2)A0(wmn2)−wmnA1(wmn2)A(wnm+n2)=A0((wnm)2)+wnm+n2A1((wnm)2)=A0(wn2m)−wnmA1(wn2m)

也就是说，只要有了A0(X)A0(X) 和A1(X)A1(X) 的点值表示，就能在Θ(n)Θ(n) 时间算出A(X)A(X) 的点值表示，对于当前层确定的位置ii ，就可以用下一层的两个值更新当前的值，我们称这个操作为“蝴蝶变换”

因为这个过程一定要求每层都可以分成两大小相等的部分，所以多项式最高次项一定是2p2p (p∈Np∈N )次方，如果不是的话，直接在最高次项补零就可以啦

于是我们有了递归的写法：

void FFT(Complex* a,int len){
    if(len==1) return;
    Complex* a0=new Complex[len/2];
    Complex* a1=new Complex[len/2];
    for(int i=0;i<len;i+=2){
        a0[i/2]=a[i];
        a1[i/2]=a[i+1];
    }
    FFT(a0,len/2);FFT(a1,len/2);
    Complex wn(cos(2*Pi/len),sin(2*Pi/len));
    Complex w(1,0);
    for(int i=0;i<(len/2);i++){
        a[i]=a0[i]+w*a1[i];
        a[i+len/2]=a0[i]-w*a1[i];
        w=w*wn;
    }
    return;
}

但递归版的FFT常数巨大，实现起来比较复杂，于是又有了迭代的写法

重新考虑下递归FFT的过程，在第ii 次求解中，我们将所有元素二进制ii 位为00 的放在了左面，ii 位为11 的放在了右面，事实上，每个元素最终到的是他二进制颠倒过来的位置

再拿一张别人的图

迭代写法：

inline void DFT(Complex a[]){
    for(int i=0;i<len;i++)///pos[i]代表反转后的位置
        if(i<pos[i])
            swap(a[i],a[pos[i]]);
    for(int i=2,mid=1;i<=len;i<<=1,mid<<=1){///len代表多项式最高次项
        ///第一层i是枚举合并到了哪一层。
        Complex wm(cos(2.0*pi/i),sin(2.0*pi/i));
        for(int j=0;j<len;j+=i){///第二层j是枚举合并区间。
            Complex w(1,0);
            for(int k=j;k<j+mid;k++,w=w*wm){///第三层k是枚举区间内的下标。
                Complex l=a[k],r=w*a[k+mid];
                a[k]=l+r;a[k+mid]=l-r;
            }
        }
    }
    return;
}

• 插值

有人证出来插值只要将所有wmnwnm 换成wm+n2nwnm+n2 ，也就是所有的虚部取相反数，再将最终结果除以lenlen ，就是插值的过程了

究竟为什么？我觉得人生一定要有点遗憾可以参考这里，我就不多说了

支持插值的迭代写法：

const double DFT=2.0,IDFT=-2.0;///进行求值，第二个参数传DFT，插值传IDFT
inline void FFT(Complex a[],double mode){
    for(int i=0;i<len;i++)
        if(i<pos[i])
            swap(a[i],a[pos[i]]);
    for(int i=2,mid=1;i<=len;i<<=1,mid<<=1){
        Complex wm(cos(2.0*pi/i),sin(mode*pi/i));
        for(int j=0;j<len;j+=i){
            Complex w(1,0);
            for(int k=j;k<j+mid;k++,w=w*wm){
                Complex l=a[k],r=w*a[k+mid];
                a[k]=l+r;a[k+mid]=l-r;
            }
        }
    }
    if(mode==IDFT)
        for(int i=0;i<len;i++)
            a[i].x/=len;
    return;
}

现在，你已经会写FFT了！

生成函数

小AA 有aiai 个价值为AiAi 的物品，小BB 有bibi 个价值为AiAi 的物品，求用两个组成价值为cici 的方案数

生成函数可以解决上面的这个问题，构造两个多项式，第ii 项表示价值为ii 的物品有多少个，对两个人分别构造，乘在一起的多项式就代表所有的方案数了

NTT——快速数论变换

当FFT需要取模时，复数的存在就特别尴尬了，有没有什么东西可以代替单位根呢？

原根性质：假设g​g​ 是素数p​p​ 的一个原根，则g1,g2,...,g(p−1)​g1,g2,...,g(p−1)​ 在模p​p​ 意义下两两不同，且结果恰好为1​1​ ~p−1​p−1​

wnn≡g(p−1)≡1(mod p)wnn≡g(p−1)≡1(mod p) (中间那个是费马小定理)

所以可以把g(p−1)/ng(p−1)/n 看成w1nwn1 的等价。

但这种质数必须是NTT质数(费马质数)，即(p−1)(p−1) 有超过序列长度的2的正整数幂因子的质数

具体证明还是看这里吧

参考资料：
Pick’s blog
Fenghr的博客
Miskcoo’s Space