图的最小生成树之Prim算法及Kruskal算法

最小生成树

• 定义：无向图连通图G中，由所有顶点构成且总价值（连接权值和）最低的一棵树（拓扑结构）称为一个最小生成树。
• 最小生成树顶点为|V|个，边数为|V|-1，没有圈。
• 对任一生成树T，如果将图中一条不属于T的边添加至T，则会产生一个圈，从该圈中除去任意一条边，则会又恢复成生成树。
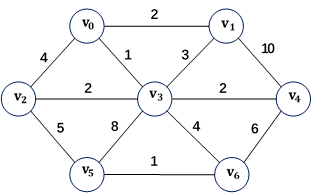
• 下图为一示例：
  
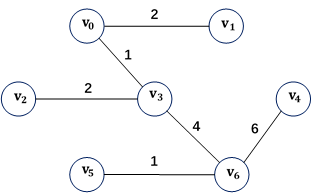
• 对于上面的无向有权连通图，其最小生成树为：
  
• 解决最小生成树问题有两种算法Prim算法和Kruskal算法，二者都是基于贪心算法的策略。

---

Prim算法

• 由于最小生成树包含图中所有顶点。因此可以从顶点以及顶点间的连接权值考虑解决问题。
• Prim算法考虑顶点以及邻接点，每一步基于贪心的策略，选取未知的且与已知顶点具有最小连接权值的顶点。
• Prim算法和求带权最短路径Dijkstra算法一样，借助一个状态信息表InfoTable来标记每一步每个顶点的状态。
• InfoTable中，每个顶点有三个状态：Known（标记顶点是否被声明已知），dist（与开始顶点的距离），Path（上一个被标记已知的顶点）。
• 与Dijkstra不同的是，这里的状态信息表更新规则为：在每个顶点v被选取以后，对于每个未知的v邻接点，$dist_w = min(dist_w, weight_{v,w})$。另外Prim算法运行在无向图上，注意每条边出现在两个邻接表中。
• Prim算法运行时间复杂度为$O(|V|^2)$，使用二叉堆时，运行时间为$O(|E|\log |V|)$。

template<class T>
void Graph<T>::Prim(int index)      // Prim算法实现，目的是为了改变index顶点的状态信息表
{
    int MinIndex;
    while (1)
    {
        MinIndex = UnknownMinDistVertex(index);     // 寻找当前index顶点的状态信息表的最小dist值的顶点下标
        if (MinIndex == -1)                         // 当MinIndex为-1，表示所有点都被标明已知，结束循环
            break;
        VSet[index].table[MinIndex].Known = true;       // 标记最小dist值的顶点为已知
        // 遍历当前最小dist值的顶点的邻接表
        for (vector<Vertex<T>>::iterator iter = VSet[MinIndex].adj_list.begin(); iter != VSet[MinIndex].adj_list.end();iter++)
        {
            if (!VSet[index].table[iter->value].Known)  // 如果其邻接点未被声明已知，则
                // 如果最小dist顶点与其邻接点的连接权值小于其邻接点原有的dist值，则更新其邻接点的dist值
                if (iter->weight < VSet[index].table[iter->value].dist)
                {
                    VSet[index].table[iter->value].dist = iter->weight;
                    // 更新最小dist顶点的邻接点的Path值为最小dist顶点（的值，为了方便）
                    VSet[index].table[iter->value].Path = VSet[MinIndex].value;     
                }
        }
    }
}

---

Kruskal算法

• Kruskal算法同样采取贪心的策略来解决最小生成树问题。和Prim不同的是，Kruskal算法考虑图中的每条边。
• Kruskal每次选择具有最小连接权值的边，当每次选择的边与已被选择的边不构成圈时，就选定该条边。
• 当选定的边数到达一定数目|V|-1时，算法终止，所有边会形成一个树即最小生成树。
• 判断是否形成圈：首先所有顶点各自构成一个集合，当它们之间的边被选定时，合并成一个大集合。算法进行到某一刻时，两个顶点u，v属于同一个集合当且仅当它们连通，如果下一步再出现一条边的两个顶点已经在集合中，则会形成一个圈，则不选择这条边。
• Kruskal算法每次要寻找一条最小权值边，时间复杂度为$O(|E|^2)$，如果采用堆，时间复杂度为$O(|E|\log |E|)$，由于$|E|=O(|V|^2)$，因此$O(|E|\log |E|)=O(|E|\log |V|)$。

template<class T>
multiset<Edge<T>> Kruskal(Graph<T> G)           // Kruskal算法求图的最小生成树
{
    multiset<Edge<int>> EdgeSet;        // 创建一个边集合储存图中每条边，边的权值可以相等，因此用multiset

    for (int i = 0;i < G.getsize() - 1;i++)
    {
        for (int j = 0;j < G.VSet[i].adj_list.size();j++)   // 扫描邻接点
        {
            // 顶点的值是等于自身序号且递增的，由于无向图，这样避免选边重复
            if (G.VSet[i].adj_list[j].value > G.VSet[i].value)
            {
                Edge<int> temp_edge;    // 创建临时边
                temp_edge.v = G.VSet[i];  temp_edge.u = G.VSet[i].adj_list[j];  // 临时边顶点
                temp_edge.weight = G.VSet[i].adj_list[j].weight;        // 权值
                EdgeSet.insert(temp_edge);                  // 将临时边存至向量Edges中
            }
        }
    }

    set<Vertex<int>> UVSet1;        // 创建两个不相交集合保存被选中边的顶点
    set<Vertex<int>> UVSet2;
    multiset<Edge<int>> ReturnSet;      // 最小生成树边集合
    Edge<int> MinEdge;              // 创建当前最小权值边变量

    MinEdge = *EdgeSet.begin();     // 取边集合首元素即最小权值边

    EdgeSet.erase(EdgeSet.begin());         // 删除首元素
    UVSet1.insert(MinEdge.u);
    UVSet1.insert(MinEdge.v);               // 首先将最小权值边顶点插入之UVSet1里面
    ReturnSet.insert(MinEdge);      // 选定当前最小边至ResultEdgeSet

    while (UVSet1.size() != G.getsize())        //当被选边顶点集合点数不等于图点数时执行循环 
    {
        if (!EdgeSet.empty())                   // 如果边集合不为空
        {
            MinEdge = *EdgeSet.begin();         // 取边集合首元素即当前最小权值边
            EdgeSet.erase(EdgeSet.begin());     // 删除首元素
        }
        set<Vertex<int>>::iterator iter1 = UVSet1.find(MinEdge.u.value);    // 在UVSet1中查找待选边的u顶点
        set<Vertex<int>>::iterator iter2 = UVSet1.find(MinEdge.v.value);    // 在UVSet1中查找待选边的v顶点
        if ((iter1 == UVSet1.end() && iter2 != UVSet1.end()) || (iter2 == UVSet1.end() && iter1 != UVSet1.end()))   // 当且仅当只有一个顶点在UVSet1中
        {
            ReturnSet.insert(MinEdge);  // 选择该条边
            UVSet1.insert(MinEdge.u);
            UVSet1.insert(MinEdge.v);   // 两个顶点插入UVSet1中，set中重复元素不会插入，故如果该条边有一个顶点已经在UVSet1中，则不会重复插入
            if (UVSet2.find(MinEdge.u.value) != UVSet2.end() || UVSet2.find(MinEdge.u.value) != UVSet2.end())   // 如果边两个顶点有一个在UVSet2中
            {
                for (set<Vertex<int>>::iterator iter = UVSet2.begin();iter != UVSet2.end(); iter++)             // 合并两个集合
                {
                    UVSet1.insert(*iter);
                }
            }
        }
        else if (iter1 == UVSet1.end() && iter2 == UVSet1.end())                // 如果两个顶点都不在UVSet1中
        {

            ReturnSet.insert(MinEdge);  // 选定该条边
            UVSet2.insert(MinEdge.u);
            UVSet2.insert(MinEdge.v);   // 两个顶点插入UVSet2中
        }
    }
    return ReturnSet;
}

• 该例中，采用STL模板库中set模板来存放边集合及点集合，set模板基于一种红黑树的平衡二叉树的数据结构，能够实现堆的时间复杂度。

---

附图最小生成树之Prim算法示例C++

#include<iostream>
#include<vector>
#include<stack>
#include<queue>
#include<iterator>
using namespace std;

const int INF = 999999;     // 表示无穷大（此例中）

template<class T> class Vertex;             // 提前声明顶点类

template<class T>
class InfoTable {       // 创建一个信息表类
public:
    bool Known;         // 是否被遍历
    int dist;           // 顶点间的距离
    T Path;     // 用顶点关键字表示的路径栏
};

template<class T>
class Vertex {      // 创建一个顶点类
public:
    T value;        // 顶点的关键字值
    vector<Vertex<T>> adj_list;     // 顶点的邻接表
    InfoTable<T>* table;        // 最短路径时每个顶点的信息栏
    int weight;     // 顶点之间的权重（相邻顶点的连接权值），存放在邻接顶点中，每个顶点与自身的权值为0
    Vertex(T value = 0) :value(value), weight(0) {} // 默认构造函数
};


template<class T>
class Graph {       // 创建一个图类
public:
    vector<Vertex<T>> VSet;     // 表示顶点的集合
    Graph(int sz) :size(sz) {}  // 构造函数

    void Construct();       // 创建（无向）图
    void InitInfoTable(int index);      // 初始化图中顶点的状态信息表

    int UnknownMinDistVertex(int index);    // 找index状态信息表中未知的（Known=0）最小dist顶点（的下标）
    void Prim(int index);       // Prim算法求图的最小生成树，以index顶点开始
    void PrintMinSpanTree(int index);       // 打印最小生成树

private:
    int size;                   // 图中顶点的个数
};

template<class T>
void Graph<T>::InitInfoTable(int index)     // 初始化图中index顶点的状态信息表
{
    VSet[index].table = new InfoTable<T>[size]; // 为每个顶点的状态表申请空间
    for (int i = 0;i < size;i++)
    {
        VSet[index].table[i].Known = false;     // 每个节点都没被经过
        VSet[index].table[i].dist = INF;        // 初始时每个顶点距离为无穷，表示不可达
        VSet[index].table[i].Path = -1;
    }
    VSet[index].table[index].dist = 0;              // 初始时每个顶点距离自身为0

}

template<class T>
int Graph<T>::UnknownMinDistVertex(int index)
{
    int MinIndex = -1;  // 初始化未知最小dist顶点下标为-1
    for (int i = 0;i < size;i++)
    {
        if (!VSet[index].table[i].Known)        // 首先找到第一个未知的顶点
            MinIndex = i;                       // 如果未知点（未被声明已知的顶点）存在，则更新MinIndex的值
    }

    for (int i = 0;i < size;i++)                // 再一次遍历index顶点的状态信息表
    {
        // 当某个顶点的dist小于当前最小dist值且未知
        if (VSet[index].table[i].dist < VSet[index].table[MinIndex].dist && !VSet[index].table[i].Known)
            MinIndex = i;               // 更新最小dist值下标
    }
    return MinIndex;
}

template<class T>
void Graph<T>::Prim(int index)      // Prim算法实现，目的是为了改变index顶点的状态信息表
{
    int MinIndex;
    while (1)
    {
        MinIndex = UnknownMinDistVertex(index);     // 寻找当前index顶点的状态信息表的最小dist值的顶点下标
        if (MinIndex == -1)                         // 当MinIndex为-1，表示所有点都被标明已知，结束循环
            break;
        VSet[index].table[MinIndex].Known = true;       // 标记最小dist值的顶点为已知
        // 遍历当前最小dist值的顶点的邻接表
        for (vector<Vertex<T>>::iterator iter = VSet[MinIndex].adj_list.begin(); iter != VSet[MinIndex].adj_list.end();iter++)
        {
            if (!VSet[index].table[iter->value].Known)  // 如果其邻接点未被声明已知，则
                // 如果最小dist顶点与其邻接点的连接权值小于其邻接点原有的dist值，则更新其邻接点的dist值
                if (iter->weight < VSet[index].table[iter->value].dist)
                {
                    VSet[index].table[iter->value].dist = iter->weight;
                    VSet[index].table[iter->value].Path = VSet[MinIndex].value;     // 更新最小dist顶点的邻接点的Path值为最小dist顶点（的值，为了方便）
                }
        }
    }
}


template<class T>
void Graph<T>::PrintMinSpanTree(int index)
{
    cout << "The InfoTable of V" << index << " is:\n";
    cout << "Vertex Known   dist    Path" << endl;
    for (int i = 0;i < size;i++)    // 打印下标为index的顶点的状态表
    {
        cout << "V" << i << "\t" << VSet[index].table[i].Known << "\t" << VSet[index].table[i].dist
            << "\t" << "V" << VSet[index].table[i].Path << endl;
    }
    cout << "\nPrint the edges of the minimum spanning tree: \n";   // 打印最小生成树的边
    stack<T> S;         // 借助栈输出从index顶点出发到各个顶点的无权最短路径
    int cost = 0;
    for (int i = 0;i < size;i++)
    {
        if (i == index)
            continue;
        cout << "(" << "V" << VSet[index].table[i].Path << ", V" << i << "), ";
        cost += VSet[index].table[i].dist;
    }
    cout << endl;
    cout << "The cost is: " << cost << endl;
}

template<class T>
void Graph<T>::Construct()
{
    // 创建一个点数组
    Vertex<int> V[] = { Vertex<int>(0), Vertex<int>(1), Vertex<int>(2), Vertex<int>(3),
        Vertex<int>(4), Vertex<int>(5), Vertex<int>(6) };

    // 顶点V0的邻接表
    for (int i = 1;i < 4;i++)
        V[0].adj_list.push_back(V[i]);
    V[0].adj_list[0].weight = 2;    // V0与V1的连接权值
    V[0].adj_list[1].weight = 4;    // V0与V2的连接权值
    V[0].adj_list[2].weight = 1;    // V0与V2的连接权值

    V[1].adj_list.push_back(V[0]);  // 顶点V1的邻接表
    V[1].adj_list.push_back(V[3]);
    V[1].adj_list.push_back(V[4]);
    V[1].adj_list[0].weight = 2;    // V1与V0的连接权值
    V[1].adj_list[1].weight = 3;    // V1与V3的连接权值
    V[1].adj_list[2].weight = 10;   // V1与V4的连接权值

    V[2].adj_list.push_back(V[0]);  // 顶点V2的邻接表
    V[2].adj_list.push_back(V[3]);
    V[2].adj_list.push_back(V[5]);
    V[2].adj_list[0].weight = 4;    // V2与V0的连接权值
    V[2].adj_list[1].weight = 2;    // V2与V3的连接权值
    V[2].adj_list[2].weight = 5;    // V2与V5的连接权值

                                    // 顶点V3的邻接表
    for (int i = 0;i < 7;i++)
    {
        if (i == 3)
            continue;
        V[3].adj_list.push_back(V[i]);
    }
    V[3].adj_list[0].weight = 1;    // V3与V0的连接权值
    V[3].adj_list[1].weight = 3;    // V3与V1的连接权值
    V[3].adj_list[2].weight = 2;    // V3与V2的连接权值
    V[3].adj_list[3].weight = 7;    // V3与V4的连接权值
    V[3].adj_list[4].weight = 8;    // V3与V5的连接权值
    V[3].adj_list[5].weight = 4;    // V3与V6的连接权值

    V[4].adj_list.push_back(V[1]);  // 顶点V4的邻接表
    V[4].adj_list.push_back(V[3]);
    V[4].adj_list.push_back(V[6]);
    V[4].adj_list[0].weight = 10;   // V4与V1的连接权值
    V[4].adj_list[1].weight = 7;    // V4与V3的连接权值
    V[4].adj_list[2].weight = 6;    // V4与V6的连接权值

    V[5].adj_list.push_back(V[2]);  // 顶点V5的邻接表
    V[5].adj_list.push_back(V[3]);
    V[5].adj_list.push_back(V[6]);
    V[5].adj_list[0].weight = 5;    // V5与V2的连接权值
    V[5].adj_list[1].weight = 8;    // V5与V3的连接权值
    V[5].adj_list[2].weight = 1;    // V5与V6的连接权值

                                    // 顶点V6的邻接表
    for (int i = 3;i < 7;i++)
        V[6].adj_list.push_back(V[i]);
    V[6].adj_list[0].weight = 4;    // V6与V3的连接权值
    V[6].adj_list[1].weight = 6;    // V6与V4的连接权值
    V[6].adj_list[2].weight = 1;    // V6与V5的连接权值

    for (int i = 0;i < 7;i++)       // 将每个点储存在图中的点集VSet中
    {
        VSet.push_back(V[i]);
    }
}

int main()
{
    Graph<int> G(7);            // 创建一个图对象G
    G.Construct();              // 构造图

    int startV = 0;                 // 设置一个起始参考点
    G.InitInfoTable(startV);    // 初始化参考顶点的状态信息表
    G.Prim(startV);             // 以startV为起始的Prim算法
    G.PrintMinSpanTree(startV); // 打印最小生成树

    system("pause");
    return 0;
}

• 运行结果：

The InfoTable of V0 is:
Vertex  Known   dist    Path
V0      1       0       V-1
V1      1       2       V0
V2      1       2       V3
V3      1       1       V0
V4      1       6       V6
V5      1       1       V6
V6      1       4       V3

Print the edges of the minimum spanning tree:
(V0, V1), (V3, V2), (V0, V3), (V6, V4), (V6, V5), (V3, V6),
The cost is: 16
请按任意键继续. . .

---

附图最小生成树之Kruskal算法示例C++

#include<iostream>
#include<vector>
#include<iterator>
#include<set>
#include<algorithm>
using namespace std;
const int INF = 999999;     // 表示无穷大（此例中）

template<class T>
class Vertex {      // 创建一个顶点类
public:
    T value;        // 顶点的关键字值
    vector<Vertex<T>> adj_list;     // 顶点的邻接表
    int weight;     // 顶点之间的权重（相邻顶点的连接权值），存放在邻接顶点中，每个顶点与自身的权值为0
    Vertex(T value = 0) :value(value), weight(0) {} // 默认构造函数

    bool operator < (const Vertex<T> &v) const { return value < v.value; }  // 重载 < 操作符比较两顶点值大小
};

template<class T>
class Edge {        // 创建一个边类
public:
    Vertex<T> u;    // 顶点u
    Vertex<T> v;    // 顶点v
    int weight;     // u，v之间的连接权值

    bool operator < (const Edge<T> &e) const;   // 重载 < 操作符比较两条边大小
};

template<class T>
bool Edge<T>::operator < (const Edge<T> &e) const
{
    return weight<e.weight;
}

template<class T>
class Graph {       // 创建一个图类
public:
    vector<Vertex<T>> VSet;     // 表示顶点的集合
    Graph(int sz) :size(sz) {}  // 构造函数

    void Construct();       // 创建（无向）图

    int getsize() { return size; }
private:
    int size;                   // 图中顶点的个数
};

template<class T>
void Graph<T>::Construct()
{
    // 创建一个点数组
    Vertex<int> V[] = { Vertex<int>(0), Vertex<int>(1), Vertex<int>(2), Vertex<int>(3),
        Vertex<int>(4), Vertex<int>(5), Vertex<int>(6) };

    // 顶点V0的邻接表
    for (int i = 1;i < 4;i++)
        V[0].adj_list.push_back(V[i]);
    V[0].adj_list[0].weight = 2;    // V0与V1的连接权值
    V[0].adj_list[1].weight = 4;    // V0与V2的连接权值
    V[0].adj_list[2].weight = 1;    // V0与V2的连接权值

    V[1].adj_list.push_back(V[0]);  // 顶点V1的邻接表
    V[1].adj_list.push_back(V[3]);
    V[1].adj_list.push_back(V[4]);
    V[1].adj_list[0].weight = 2;    // V1与V0的连接权值
    V[1].adj_list[1].weight = 3;    // V1与V3的连接权值
    V[1].adj_list[2].weight = 10;   // V1与V4的连接权值

    V[2].adj_list.push_back(V[0]);  // 顶点V2的邻接表
    V[2].adj_list.push_back(V[3]);
    V[2].adj_list.push_back(V[5]);
    V[2].adj_list[0].weight = 4;    // V2与V0的连接权值
    V[2].adj_list[1].weight = 2;    // V2与V3的连接权值
    V[2].adj_list[2].weight = 5;    // V2与V5的连接权值

                                    // 顶点V3的邻接表
    for (int i = 0;i < 7;i++)
    {
        if (i == 3)
            continue;
        V[3].adj_list.push_back(V[i]);
    }
    V[3].adj_list[0].weight = 1;    // V3与V0的连接权值
    V[3].adj_list[1].weight = 3;    // V3与V1的连接权值
    V[3].adj_list[2].weight = 2;    // V3与V2的连接权值
    V[3].adj_list[3].weight = 7;    // V3与V4的连接权值
    V[3].adj_list[4].weight = 8;    // V3与V5的连接权值
    V[3].adj_list[5].weight = 4;    // V3与V6的连接权值

    V[4].adj_list.push_back(V[1]);  // 顶点V4的邻接表
    V[4].adj_list.push_back(V[3]);
    V[4].adj_list.push_back(V[6]);
    V[4].adj_list[0].weight = 10;   // V4与V1的连接权值
    V[4].adj_list[1].weight = 7;    // V4与V3的连接权值
    V[4].adj_list[2].weight = 6;    // V4与V6的连接权值

    V[5].adj_list.push_back(V[2]);  // 顶点V5的邻接表
    V[5].adj_list.push_back(V[3]);
    V[5].adj_list.push_back(V[6]);
    V[5].adj_list[0].weight = 5;    // V5与V2的连接权值
    V[5].adj_list[1].weight = 8;    // V5与V3的连接权值
    V[5].adj_list[2].weight = 1;    // V5与V6的连接权值

                                    // 顶点V6的邻接表
    for (int i = 3;i < 7;i++)
        V[6].adj_list.push_back(V[i]);
    V[6].adj_list[0].weight = 4;    // V6与V3的连接权值
    V[6].adj_list[1].weight = 6;    // V6与V4的连接权值
    V[6].adj_list[2].weight = 1;    // V6与V5的连接权值

    for (int i = 0;i < 7;i++)       // 将每个点储存在图中的点集VSet中
    {
        VSet.push_back(V[i]);
    }
}

template<class T>
multiset<Edge<T>> Kruskal(Graph<T> G)           // Kruskal算法求图的最小生成树
{
    multiset<Edge<int>> EdgeSet;        // 创建一个边集合储存图中每条边，边的权值可以相等，因此用multiset

    for (int i = 0;i < G.getsize() - 1;i++)
    {
        for (int j = 0;j < G.VSet[i].adj_list.size();j++)   // 扫描邻接点
        {
            // 顶点的值是等于自身序号且递增的，由于无向图，这样避免选边重复
            if (G.VSet[i].adj_list[j].value > G.VSet[i].value)
            {
                Edge<int> temp_edge;    // 创建临时边
                temp_edge.v = G.VSet[i];  temp_edge.u = G.VSet[i].adj_list[j];  // 临时边顶点
                temp_edge.weight = G.VSet[i].adj_list[j].weight;        // 权值
                EdgeSet.insert(temp_edge);                  // 将临时边存至向量Edges中
            }
        }
    }

    set<Vertex<int>> UVSet1;        // 创建两个不相交集合保存被选中边的顶点
    set<Vertex<int>> UVSet2;
    multiset<Edge<int>> ReturnSet;      // 最小生成树边集合
    Edge<int> MinEdge;              // 创建当前最小权值边变量

    MinEdge = *EdgeSet.begin();     // 取边集合首元素即最小权值边

    EdgeSet.erase(EdgeSet.begin());         // 删除首元素
    UVSet1.insert(MinEdge.u);
    UVSet1.insert(MinEdge.v);               // 首先将最小权值边顶点插入之UVSet1里面
    ReturnSet.insert(MinEdge);      // 选定当前最小边至ResultEdgeSet

    while (UVSet1.size() != G.getsize())        //当被选边顶点集合点数不等于图点数时执行循环 
    {
        if (!EdgeSet.empty())                   // 如果边集合不为空
        {
            MinEdge = *EdgeSet.begin();         // 取边集合首元素即当前最小权值边
            EdgeSet.erase(EdgeSet.begin());     // 删除首元素
        }
        set<Vertex<int>>::iterator iter1 = UVSet1.find(MinEdge.u.value);    // 在UVSet1中查找待选边的u顶点
        set<Vertex<int>>::iterator iter2 = UVSet1.find(MinEdge.v.value);    // 在UVSet1中查找待选边的v顶点
        if ((iter1 == UVSet1.end() && iter2 != UVSet1.end()) || (iter2 == UVSet1.end() && iter1 != UVSet1.end()))   // 当且仅当只有一个顶点在UVSet1中
        {
            ReturnSet.insert(MinEdge);  // 选择该条边
            UVSet1.insert(MinEdge.u);
            UVSet1.insert(MinEdge.v);   // 两个顶点插入UVSet1中，set中重复元素不会插入，故如果该条边有一个顶点已经在UVSet1中，则不会重复插入
            if (UVSet2.find(MinEdge.u.value) != UVSet2.end() || UVSet2.find(MinEdge.u.value) != UVSet2.end())   // 如果边两个顶点有一个在UVSet2中
            {
                for (set<Vertex<int>>::iterator iter = UVSet2.begin();iter != UVSet2.end(); iter++)             // 合并两个集合
                {
                    UVSet1.insert(*iter);
                }
            }
        }
        else if (iter1 == UVSet1.end() && iter2 == UVSet1.end())                // 如果两个顶点都不在UVSet1中
        {

            ReturnSet.insert(MinEdge);  // 选定该条边
            UVSet2.insert(MinEdge.u);
            UVSet2.insert(MinEdge.v);   // 两个顶点插入UVSet2中
        }
    }
    return ReturnSet;
}

int main()
{
    Graph<int> G(7);            // 创建一个图对象G
    G.Construct();              // 构造图

    multiset<Edge<int>> MSTEdgeSet = Kruskal(G);    // 求最小生成树边集合

    int cost = 0;
    cout << "The minmum spanning tree's Edge set by Kruskal algorithm is: " << endl;
    for (multiset<Edge<int>>::iterator iter = MSTEdgeSet.begin();iter != MSTEdgeSet.end();iter++)
    {
        cout << "(V" << iter->u.value << ", V" << iter->v.value << "):" << iter->weight << ", ";
        cost += iter->weight;
    }
    cout << "\nThe cost of the minmun spanning tree is: " << cost << endl;
    cout << endl;

    system("pause");
    return 0;
}

• 运行结果：

The minmum spanning tree's Edge set by Kruskal algorithm is:
(V3, V0):1, (V6, V5):1, (V1, V0):2, (V3, V2):2, (V6, V3):4, (V6, V4):6,
The cost of the minmun spanning tree is: 16

请按任意键继续. . .

---

参考资料

Mark Allen Weiss: 数据结构与算法分析