卡尔曼滤波算法实例剖析--机器人足球赛场中的定位算法

声明：本博客转载自东方赤龙知行合一，谢谢博主的分享！！！（转载仅供个人学习）

卡尔曼滤波（Kalman filtering）最早在阿波罗飞船的导航电脑中使用，它对阿波罗计划的轨道预测很有用。

卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。是目前应用最为广泛的滤波方法, 在通信, 导航, 制导与控制等多领域得到了较好的应用。

卡尔曼滤波本身是贝叶斯滤波体系的，建立在马尔科夫概率模型基础上。大多数关于卡尔曼滤波的文章都是大量的数学概率公式，看的晕头转向。本文通过机器人足球场上的定位来通俗易懂的讲述该滤波算法原理。

1. 机器人足球场景介绍

如图1所示，踢球的机器人为差分轮式机器人，它可以直线或者弧线行走，也就是可以同时以线速度v和角速度ω行动。v和ω都是从传感器测量得到的，这里认为是已知的。

如图2，足球场为矩形，内部填充灰色的黑色圆圈代表机器人，它在场内的位置可以表示为(x,y)，左下角为原点; 圆圈的黑色直线代表机器人的角度为 θ，以X轴正向为0度，逆时针旋转。

为了便于定位，四个角落和中间两边分别放置一个ROS的AR标签，这些标签完全不同，编号为 1-6, 位置在系统内已知固定。无论在场内任何地方，机器人使用Kinnect或XTionPRO 均可以探测到至少一个AR标签，ROS可以检测到距离AR标签的距离 r 和角度 φ. 它们也是实时获取的已知量。

很明显，角度θ+φ 是可以从机器人位置(x,y)和AR标签位置(mx,my)同反正切 atan2(mx - x ,my - y) 轻松计算出来。

图1 机器人足球场地实景图

图2 机器人足球场逻辑图

2. 卡尔曼滤波模型

在任何一个时间点t-1, 机器人的位置为(x, y,θ) , 它以线速度和角速度(vt,ωt)以弧线轨迹移动到下一个时间点t时，新的位置(x', y', θ')通过简单的三角函数数学公式是可以算出来的：

公式1 坐标转移矩阵

这个过程叫做状态转移，状态x=(x,y) 代表机器人的坐标（状态x 和坐标里面的x只是巧合同一个字母，因为卡尔曼滤波里面的状态就是用x表示的，不要混淆）。

按照公式1不停地累计计算从t 到 t-1，再到t+2,......,t+n，貌似可以得到机器人的实际位置。但是实际效果是什么样子呢？来看一下图3，机器人从左下角开始移动6个时间点，依次经过AR标签2-6, 它的轨迹为实线，白色圆圈代表每个时间点的位置。而根据公式1的方法计算得到的轨迹为虚线所示，灰色圆圈代表计算机算出的位置。可以清楚的看到，计算误差很大，从一开始的位置计算就有有误差，这种误差不断积累，最终‘失之毫厘，谬以千里’。

图3 移动机器人的计算轨迹（虚线）和实际轨迹（实线）有很大误差

这是为毛呢？原因就是目前所有人类制造的各种仪器都是有误差的。就像GPS定位一样，它也不是能够精确的给出一个坐标，它有个5米到10米的误差。同样机器人传感器得到的线速度v和角速度ω都是不准确的，有噪音。如图4所示，灰色圆圈为公式1计算出来的坐标，但是噪音范围为椭圆形所示，真实位置在里面的任何一点都是有可能的，只是每个点的概率不一样，中间的概率是最高的。

图4 测量误差--椭圆区域

2.1 卡尔曼滤波能做什么

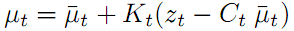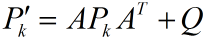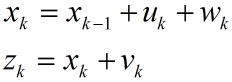
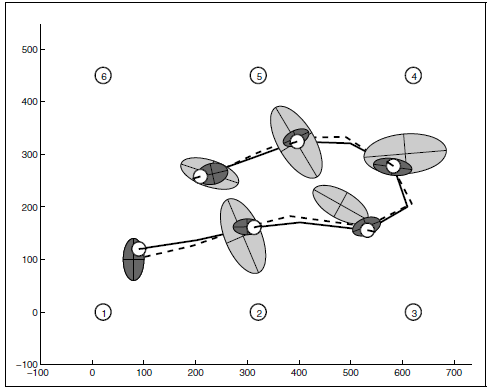
看到这里会问了，不是还有AR标签帮助测量定位吗？根据标签位置，距离和角度也可以算出坐标啊! 没错，但是还是那个老问题，这个测量结果也是有误差的，误差大小完全取决于传感器。

我们总结一下，现在有两个已知量：

移动的速度和起点坐标根据公式1算出来的坐标 x = (x,y) 有很大误差噪音
AR标签测量的值 z=(r, φ) 有很大误差噪音

卡尔曼滤波能做什么？它可以根据上面的两个有噪音的测量值融合到一起获得最优的坐标，也就是最优状态。这就是一个降噪的过程，滤波出来的坐标也是有噪音的，但是很小。如图5所示，滤波后的轨迹和真实轨迹非常接近了。灰色椭圆是测量位置的噪音范围，黑色椭圆是卡尔曼滤波后的噪音范围，确实降噪了不少。

这个最优的坐标和噪音到了下一个时刻t+1，就作为滤波的输入结合t+1的AR标签观测量和噪音再次推导一遍。机器人不断行走，该算法不断的循环执行就推导出了最优的移动轨迹。每次间隔Δt越小，滤波的精度就越高。所以计算机性能越好，就可以越精确的估计移动轨迹。

图5 卡尔曼滤波效果图移动机器人的计算轨迹（虚线）和实际轨迹（实线）非常接近

===========接下来开始讲概率矩阵数学===========

2.2 卡尔曼滤波模型参数定义

卡尔曼滤波是为了获取每个时刻t最优的状态，它有许多物理意义的参数：

状态 x = 坐标 (x,y,θ)
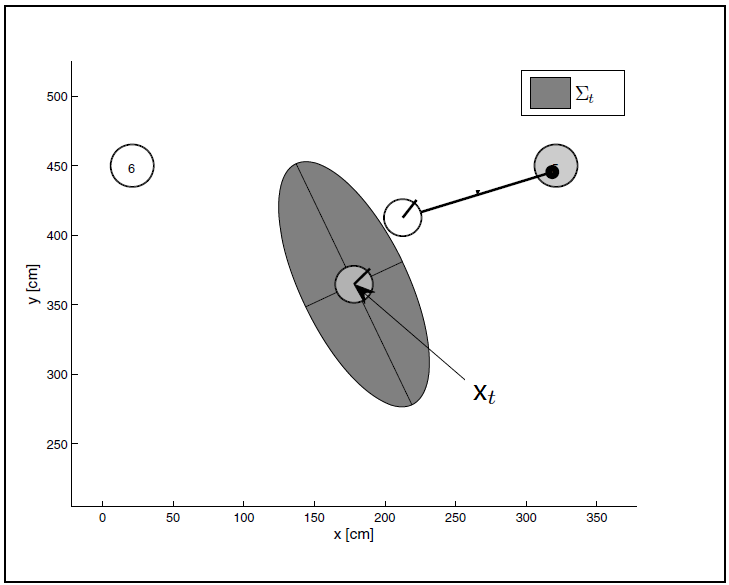
状态噪音Σ = 状态 x 的精确度
最优状态 μ 每个时刻卡尔曼滤波估算的最优坐标
状态转移控制量 u = 线速度和角速度(v, ω)
状态转移噪音 R 因为移动所增加的噪音
观测量 z = AR标签测量值 (r, φ)
观测量噪音 Q = AR标签传感器的噪音

还有几个状态转移方程:

xt =At xt-1 +Bt ut 根据t-1的坐标和移动速度估计出在t时刻的坐标，也就是上面的公式一。这里At =1，Bt 就是时间间隔 Δt
z =C x 状态量x 到观测量z 的映射关系。这里就是根据下面的三角函数计算出来的， C代表了状态映射矩阵。

2.3 卡尔曼滤波过程

有了数据，接下来就是具体操作了。科尔曼滤波或者贝叶斯滤波体系的过程都包含两个步骤：

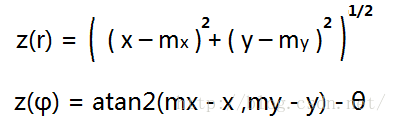
t-1 到 t时刻的状态预测，得到前验概率
根据观察量对预测状态进行修正，得到后验概率，也就是最优值

在卡尔曼滤波里面，每个状态都是一个正态分布概率，也就是高斯分布概率:

p(x) = N( μ, σ )

这里,μ 就是高斯分布的均值，也就是概率最高的值，称为最优值。σ 就是高斯分布的方差，也就是噪音。所以卡尔曼滤波最终算出来的不是一个精确的状态值，而是一个概率最高的最优状态值。这个状态值在我们的例子里面就是坐标。

2.3.1 状态预测

根据t-1时刻的最优状态值 xt-1 ，带入文章开头的状态转移方程公式1，根据控制量u得到t时刻的新状态μ。就是根据机械运动的线速度和角速度推算出新的坐标

。为了便于记忆，我们一般化它为公式一：

公式一 状态转移变换方程

上面已经说了，这个预测是有误差噪音的，在t-1时刻的噪音 Σt-1 经过状态转移后被扩大了，也就是说经过移动后，坐标的不确定性增大了。新的噪音

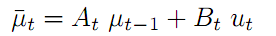
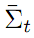。为了便于记忆，我们一般化它为公式二：

公式二状态噪音转移变换方程

2.3.2 卡尔曼增益 K

公式三 卡尔曼增益K

卡尔曼增益 K 相当于一个系数变换矩阵，它包含了两个信息：

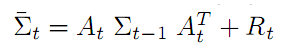
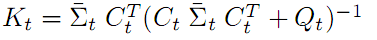
观测量 z 到状态量 x 的的变换矩阵，就是说 x = K z . 相当于2.1节提到的状态转移方程 z = C x 中 C 的逆矩阵。本文例子就相当于从地标AR标签的距离和角度反推出机器人的位置。
对观测量的可信度百分比。观测量可信度越高，也就是测量噪音Q相对于与状态预测噪音越小，该百分比就越高。反之则越低。

2.3.3 后验值修正

既然预测不准确，那就用测量后验值去修正它。先修正状态值x，就是公式四：

公式四状态修正方程

这个方程直观上很容易理解，就是假设预测状态

正确，那它观测到AR标签时的距离和角度对应的值就是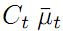

，可视为预测观测值。而

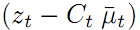则代表预测观测值与实际观测值的差距。乘上卡尔曼增益K，就得到了修正量。修正量加上预测值就是修正值或最优值。假设

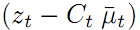为0，就是说预测AR标签位置和观测到的AR标签位置完全一样，那公式四返回就是预测状态坐标值，和直观常识吻合的非常完美。假设

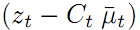的值比较大，就是说预测AR标签位置和观测到的AR标签位置差别很大，那根据卡尔曼增益K中的百分比信息的小或大，公式四就返回值靠近预测值或靠近测量值多一些，和实际物理意义吻合的还是非常完美。

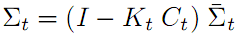
有了修正后的状态坐标值，就需要得到该状态坐标的修正后的噪音大小 Σt 就是公式五：

公式五状态误差噪音修正方程
修正后的噪音Σt 其值要比预测噪音

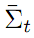和感测噪音Q都要小。这样直观上也容易理解，滤波后的状态噪音最小，所以最优。

2.4 卡尔曼滤波总结

以上公式一二三四五，就是卡尔曼滤波的五项公式。前面说过，在卡尔曼滤波里面，每个状态都是一个正态分布概率，也就是高斯分布概率:

p(x) = N( μ, σ )

整个滤波过程从高斯曲线上看就如下图6所示：

图6 卡尔曼滤波的高斯分布动态过程

a）初始时刻t-1的状态概率高斯分布，分布图的宽度越宽，误差越大，最优均值概率就越低。

b） t时刻观测到观测量概率高斯分布图，明显观测量噪音低，可信度高。但是两个高斯的均值不一致，就是说观测和预估不一致

c）卡尔曼滤波后的高斯分布图，该高斯图的噪音比其它两个都小，最优均值概率高于其它两个高斯图，而均值恰好在其它两个高斯均值之间

d） t+1时刻发生的状态转移，状态向右移动，这个过程增加了新的噪音，所以新的状态高斯图噪音增大，最优均值概率下降

e） t+1时刻的观测量高斯分布图

f） t+1时刻应用卡尔曼滤波融合出来噪音低的最优状态高斯图

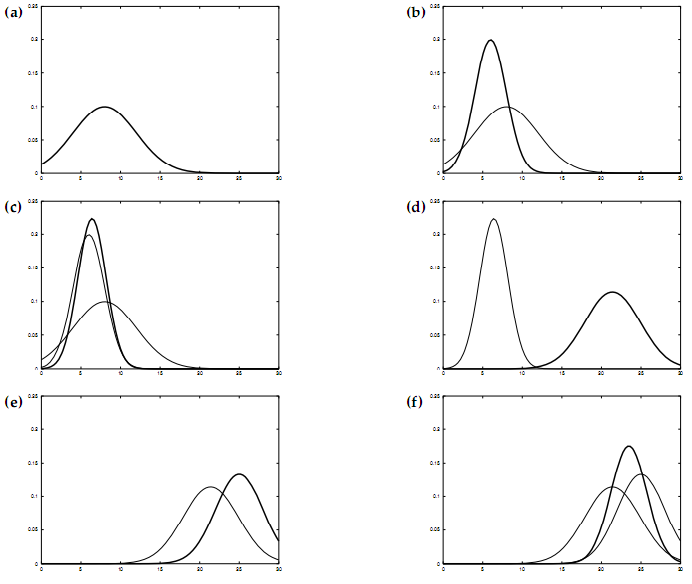
3 科尔曼滤波的条件和扩展卡尔曼滤波

本文的例子其实是个扩展卡尔曼滤波。标准的卡尔曼滤波要求2.2小节中的两个状态转移方程为线性方程，也就是要求A、B和C矩阵都为线性矩阵。

xt = At xt-1 + Bt ut 根据t-1的坐标和移动速度估计出在t时刻的坐标，也就是上面的公式一。这里At =1，Bt 就是时间间隔 Δt
z = C x 状态量x 到观测量z 的映射关系。这里就是根据下面的三角函数计算出来的， C代表了状态映射矩阵。

本文的例子明显不符合这个要求，因为涉及到了三角函数等计算。标准卡尔曼滤波在现实环境中是很难找到的，大部分情况下都是非线性状态转移。而扩展卡尔曼滤波就是应用在非线性状态转移的环境中的。它的算法和标准算法一样，只是把上面的A、B和C矩阵线性化，也就是用一个线性方程最大程度的逼近非线性方程。常用的方法有UT变换( Unscented Transformation) 和UKF变换。

===========接下来为数据仿真实验===========

参考知行合一

这部分主要是通过对第一部分中提到的匀加速小车模型进行位移预测。

先来看看状态方程能建立准确的时候，状态方程见第一部分分割线以后内容，小车做匀加速运动的位移的预测仿真如下。

clc
clear all
close all

% 初始化参数
delta_t=0.1;   %采样时间
t=0:delta_t:5;
N = length(t); % 序列的长度
sz = [2,N];    % 信号需开辟的内存空间大小  2行*N列  2:为状态向量的维数n
g=10;          %加速度值
x=1/2*g*t.^2;      %实际真实位置
z = x + sqrt(10).*randn(1,N); % 测量时加入测量白噪声

Q =[0 0;0 9e-1]; %假设建立的模型  噪声方差叠加在速度上 大小为n*n方阵 n=状态向量的维数
R = 10;    % 位置测量方差估计，可以改变它来看不同效果  m*m      m=z(i)的维数

A=[1 delta_t;0 1];  % n*n
B=[1/2*delta_t^2;delta_t];
H=[1,0];            % m*n

n=size(Q);  %n为一个1*2的向量  Q为方阵
m=size(R);

% 分配空间
xhat=zeros(sz);       % x的后验估计
P=zeros(n);           % 后验方差估计  n*n
xhatminus=zeros(sz);  % x的先验估计
Pminus=zeros(n);      % n*n
K=zeros(n(1),m(1));   % Kalman增益  n*m
I=eye(n);

% 估计的初始值都为默认的0，即P=[0 0;0 0],xhat=0
for k = 9:N           %假设车子已经运动9个delta_T了，我们才开始估计
    % 时间更新过程
    xhatminus(:,k) = A*xhat(:,k-1)+B*g;
    Pminus= A*P*A'+Q;
    
    % 测量更新过程
    K = Pminus*H'*inv( H*Pminus*H'+R );
    xhat(:,k) = xhatminus(:,k)+K*(z(k)-H*xhatminus(:,k));
    P = (I-K*H)*Pminus;
end
 
figure
plot(t,z);
hold on
plot(t,xhat(1,:),'r-')
plot(t,x(1,:),'g-');
legend('含有噪声的测量', '后验估计', '真值');
xlabel('Iteration');

得到的仿真图像：

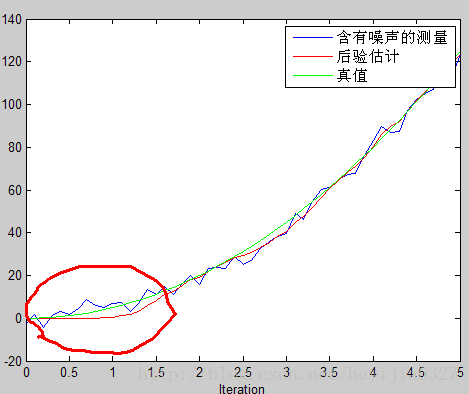
绿线为真实值，蓝色的为噪声很大的测量值，红线为估计值。由此可以看出卡尔曼滤波确实相当犀利，提供了一个顺滑的最优的估计。并请注意代码中，特地使得估计是从第9个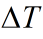才开始预测,就像雷达跟踪一样，假设一开始我们没有发现这个东西，它已经运行了一段时间，我们在雷达测量和自己预测后得到估计结果，从图中可看出效果确实很好。

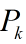
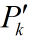
但这里请注意图像中画红圈部分，由于一开始你预测值为0，而实际上不是（它已经运动9个时间间隔了），所以估计出的效果不好。在这里回忆前面讨论过的K值大小和估计的关系，既然预测不准，那么一开始我就先相信测量呗。这就涉及估计值误差协方差初值的选取。在第一部分中我们知道卡尔曼增益K与预测误差协方差矩阵正相关，由第一部分推导知道预测误差协方差阵：

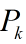
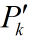
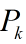
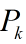
它又和估计误差协方差矩阵有关，在Q，A确定的情况下，和成正比。所以如果我们给的初值大的话，那么递推第一步中计算出的卡尔曼增益K就大。K大意味着更相信测量值。

修改初值P=[2 0;0 2],估计图像如下，可以看到初始估计明显改进了。（两幅图中，测量值相同，只改变了P）。这幅图中红色水平线那部分是前9个时间段，你还没开始雷达追踪，所以是水平的为0。

好了，到第二个问题，当状态方程建立不正确的又会怎样呢？实际应用中很多时候我们不能建立正确的状态方程。

我们假设建立的状态方程如下：

转换矩阵A,B,H都等于1.这个模型明显是不正确的。

注意这个时候的系统噪声，就不单单只是系统内部产生的，还包括你建立状态方程的不正确性。你建立的越不正确，根据你模型进行的预测就不正确，从这个角度来说，相当于你的噪声增大了。所以这个时候系统噪声W的方差应该增大。理解这一点，对改进实际估计效果有好处。接下来通过对比不同的W方差值设定给出对比，贴出这部分仿真如下。

clc
clear
close all

% 初始化参数
delta_t=0.1;
t=0:delta_t:5;
g=10;%加速度值
n_iter = length(t); % 序列的长度
sz = [n_iter, 1]; % 信号需开辟的内存空间大小
x=1/2*g*t.^2;
x=x';
z = x + sqrt(10).*randn(sz); % 测量时加入测量白噪声

Q = 0.9; % 过程激励噪声方差   
         %注意Q值得改变  待会增大到2，看看效果。对比看效果时，修改代码不要改变z的值
R = 10; % 测量方差估计，可以改变它来看不同效果
 
% 分配空间
xhat=zeros(sz);      % x的后验估计
P=zeros(sz);         % 后验方差估计
xhatminus=zeros(sz); % x的先验估计
Pminus=zeros(sz);    % 先验方差估计
K=zeros(sz);         % Kalman增益
 
% 估计的初始值
xhat(1) = 0.0;
P = 1.0;
for k = 2:n_iter   %
    % 时间更新过程
    xhatminus(k) = xhat(k-1);
    Pminus(k) = P(k-1)+Q;
    
    % 测量更新过程
    K(k) = Pminus(k)/( Pminus(k)+R );
    xhat(k) = xhatminus(k)+K(k)*(z(k)-xhatminus(k));
    P(k) = (1-K(k))*Pminus(k);
end
 
figure
plot(t,z);
hold on
plot(t,xhat,'r-')
plot(t,x,'g-');
legend('含有噪声的测量', '后验估计', '真值');
xlabel('Iteration');

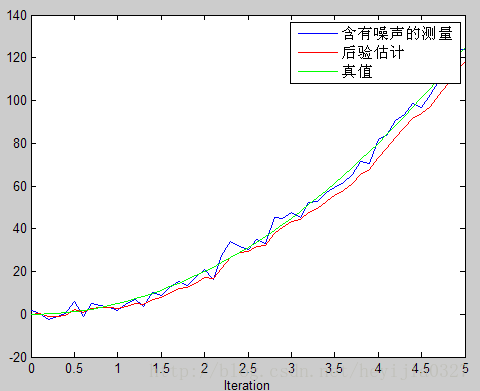
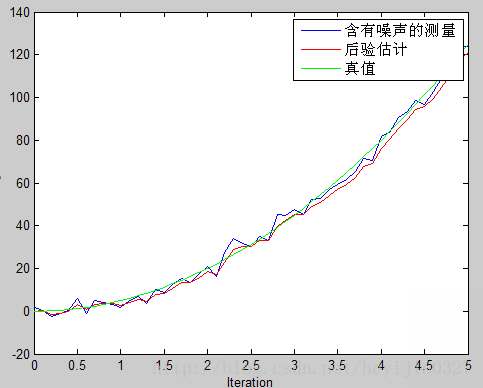
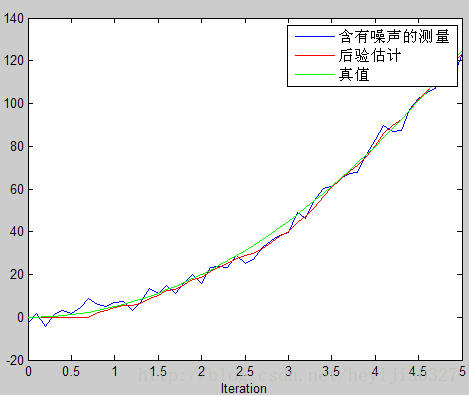
最开始假设系统噪声方差和前面状态建立正确的时候一样为0.9，估计图像如图(a)。效果不理想，我们知道状态方程建立错误了，系统噪声方差应该比之前大。于是增大系统噪声方差再预测，如图(b)

图(a)图(b)

两个图中测量值是一样的，只是第二图中将系统噪声方差Q增大到2。对比可以看出，特别是图像后半段，图(b)比图(a)效果更接近真实值。

至此，从推导到应用接近尾声了，但我在这里还有一个问题就是，你随便给的x的预测初值，模型建立也不正确，kalman filter 竟然依然这么犀利，那么他收敛性怎么证明呢？写这文章的时候，笔者没有看详细的数学证明，但是由前面说到的kalman filter和数值分析里递推求解方程组时用的Gauss-Seidel 迭代法，两者真的很相近，于是我直观的认为卡尔曼的收敛性和Gauss-Seidel 一样。Gauss-Seidel迭代法里权重的选取能使得递推收敛真实值，因此卡尔曼滤波里增益K的每次计算就是卡尔曼收敛的重要保证。

卡尔曼滤波算法实例剖析--机器人足球赛场中的定位算法

猜你喜欢