x = cos x 的解析形式
玩计算器的发现
大家都玩过计算器吧, 不知注意到没有.
输入任意数, 然后不断按最后总会输出
.
什么, 你说明明记得是:? 哦, 因为你用了角度制.
这一系列操作等价于求解方程, 角度制下就是
.
当然对于现在的你来说求数值解没啥意思了, 要求就求解析解是吧.
不过这两个方程其实是一样的, 我们先变个形:
也就是说:
于是我们现在只要解决这一个方程了.
最早研究这个问题的是天文学家, 毕竟那时候也没什么计算器给你玩, 一切要从实际出发...
开普勒方程
你可能听说过, 三体问题很困难, 直到一百多年前的庞加莱时代才被搞定.
而二体问题则简单的多, 400年前开普勒时代就研究的差不多了.
你至少知道这个成果, 两个天体以一个为交点, 另一个必定在圆锥曲线上运动.
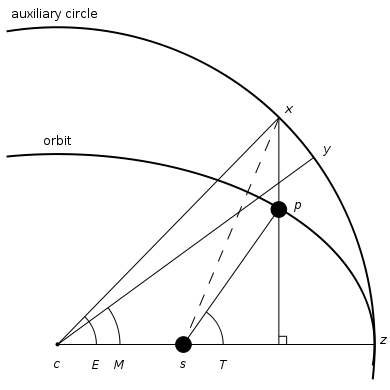
一般天体遵循椭圆轨道, 如图椭圆是实际运行的轨道, 与椭圆相切的是一个以半长轴为半径的辅助圆.
在一定的时间内, 椭圆轨道上的质点运行到了
点, 而辅助圆上的假想质点运行到了
点.
- 椭圆轨道上所转过的角度
被称为真近点角(True Anomaly)
- 辅助圆轨道上假想质点所转过的角度
被称为平近点角(Mean Anomaly)
- 将椭圆上的质点向上作延长线,交辅助圆于
点所形成的角
被称为偏近点角(Eccentric Anomaly)
天文学家发现, 它们满足如下关系式:
Kepler Equation:
抛物线就是的特殊情况, 双曲线有所不同.
Hyperbolic Kepler Equation:
但从数学上讲, 这个式子其实就是:
也就是说不考虑物理意义其实是一样的.
开普勒方程的解析解
有了方程当然接下来就是求解了咯, 古代计算力比较值钱, 毕竟没有计算机, 所以大家对解析解都有一种病态的追求.
怎么着推一天公式要比算一整天的牛顿迭代有趣吧?
作一下等价性检验:
In [] = FindRoot[x==Cos@x,{x,0}]
x-Pi/2/.FindRoot[Pi/2==x-Sin@x,{x,1}]
FindRoot[x==Cos[Pi x/180],{x,0}]
180x/Pi-90/.FindRoot[Pi/2==x-Pi Sin@x/180,{x,1}]
Out[] = 0.7390851332151605`
{x -> 0.7390851332151607`}
0.9998477415310987`
{x -> 0.9998477415310881`}
拉格朗日反演
不能分离但
, 展开
,然后直接用级数反演即可.
Mathematica 可以很方便的执行级数反演.
Series[M- Sin[M], {M, 0, 10}]//InverseSeries
Series[M-e Sin[M], {M, 0, 10}]//InverseSeries
早期解这个方程使用了关于离心率的麦克劳林展开.
这不是个整函数, 所以引入了所谓的拉普拉斯极限.
超出收敛域的部分级数失效, 级数反演则很好的解决了这个问题.
贝塞尔函数解
当然无穷级数不利于计算, 能否使用微积分表达是我们接下来的探索重点.
我们来考虑函数方程:
我们假设它可以展开为傅里叶级数, 分析原函数方程性态可以期望这是个正弦级数.
那么系数可以表达为:
我们来尝试计算, 嗯? 没思路怎么办...
无脑分部积分展开到能搞定为止呗.
而这正好是贝塞尔函数的定义式之一:
Bessel Function of the First Kind:%3D%5Cfrac%7B1%7D%7B%5Cpi%7D%5Cint_0%5E%5Cpi+%5Ccos(n+%CE%B8-z+%5Csin+%CE%B8)%5C%2C%5Cmathrm%7Bd%7D%CE%B8%5C+%3Bn%5Cin+%5Cmathbb%7BZ%7D)
于是原式可以写成
赫维茨-勒奇超越函数解
Stack Exchange上有个用反三角函数和三角函数表示的解析解, 这个解比较有难度.
特殊函数论中将以下级数称为赫维茨-勒奇超越函数(Lerch Transcendent Function)
我们从上面的贝塞尔函数解开始, 还原掉贝塞尔函数:
然后交换积分求和顺序.
里面的部分圈起来叫, 用欧拉公式展开.
其中:
可以发现其实都是的结构.
我们引入多对数函数:
也就是说:
用这个函数化简等式:
同样的整理一下:
可以合并成两组, 然后再次展开, 运算量有点大.
化简的时候注意恒等式:.
注意到第二部分:
最后代回去大功告成!
代入数据就得到了 Stack Exchange 一样的结果.
我对这种写法感到很不爽.
这个当然不能直接抵消, 由于, 我们作复展开.
严格来说这两者不是完全相等的, 因为这样一来消掉了奇点.
不过积分的时候完全可以划等号, 因为区间开闭完全不影响积分值.
综上所述, 最后代入值, 我们得到了:
(*真男人从不回头看数值验证*)
(2 + I Integrate[Log[-I/E^(I*(t - Sin[t]))], {t, 0, Pi}])/(2*Pi)//N
(Pi + 90I Integrate[Log[(-I)*E^((-I)*t + (1/180)*I*Pi*Sin[t])], {t, 0, Pi}])/Pi^2//N
> 0.7390851332151609`
> 0.9998477415310951`
只有娘们才喜欢用特殊函数
最后一个是百度贴吧上的, 这个答案就非常魔幻了,它和上面两个方法不是一个系列的, 和第一个方法有关.
暴力求解拉格朗日反演的解析形式, 场面非常的少儿不宜...
我一时半会儿也没看懂,详情看参考书目(3).
从这个结果上也能看出这个方法有多残暴...
(*怎么可以这么暴力的说*)
\[Pi]/2 Exp[NIntegrate[1/(\[Pi] x) ArcTan[((\[Pi] x+2)Log[(Sqrt[1-x^2]+1)/x]x)/(x^2Log[(Sqrt[1-x^2]+1)/x]^2-\[Pi] x-1)],{x,0,1},WorkingPrecision->50]]
ArcCot[1+1/(2\[Pi] ) NIntegrate[Log[((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]+x)^2)/((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]-x)^2)],{x,0,1},WorkingPrecision->50]]
> 0.73908513321516064165531208767387340401341175890075746496567242428255184768807`50.12267193056545
> 0.73908513321516064165531208767387340401341175890075746496567993239614795659229`51.22422170141253
参考书目
- On Taylor series and Kapteyn series of the first and second type
- Kepler's equation, radiation problems and Meissel's expansion
- An exact analytical solution of Kepler's Equation
玩计算器的发现
大家都玩过计算器吧, 不知注意到没有.
输入任意数, 然后不断按\mathtt{cos\ ANS}最后总会输出0.739085.
什么, 你说明明记得是:0.999847? 哦, 因为你用了角度制.
这一系列操作等价于求解方程x=\cos x, 角度制下就是x=\cos x°=\cos\dfrac{\pi x}{180}.
当然对于现在的你来说求数值解没啥意思了, 要求就求解析解是吧.
不过这两个方程其实是一样的, 我们先变个形:
\begin{aligned} x=\cos x\;\Longrightarrow& x-\frac{\pi}{2}=\cos \left(x-\frac{\pi}{2}\right)&=\sin x\\ x=\cos x°\Longrightarrow& \frac{180 x}{\pi }-90=\cos \left(\frac{ \pi}{180} \left(\frac{180 x}{\pi }-90\right)\right)&=\sin x \end{aligned}
也就是说:
于是我们现在只要解决Ax-B=\sin(x)这一个方程了.
最早研究这个问题的是天文学家, 毕竟那时候也没什么计算器给你玩, 一切要从实际出发...
开普勒方程
你可能听说过, 三体问题很困难, 直到一百多年前的庞加莱时代才被搞定.
而二体问题则简单的多, 400年前开普勒时代就研究的差不多了.
你至少知道这个成果, 两个天体以一个为交点, 另一个必定在圆锥曲线上运动.
一般天体遵循椭圆轨道, 如图椭圆是实际运行的轨道, 与椭圆相切的是一个以半长轴为半径的辅助圆.
在一定的时间t内, 椭圆轨道上的质点运行到了p点, 而辅助圆上的假想质点运行到了y点.
椭圆轨道上所转过的角度\angle T被称为真近点角(True Anomaly)
辅助圆轨道上假想质点所转过的角度\angle M被称为平近点角(Mean Anomaly)
将椭圆上的质点向上作延长线,交辅助圆于x点所形成的角\angle E被称为偏近点角(Eccentric Anomaly)
天文学家发现, 它们满足如下关系式:
Kepler Equation:M= E-\epsilon \sin(E)
抛物线就是\epsilon=1的特殊情况, 双曲线有所不同.
Hyperbolic Kepler Equation:M = \epsilon \sinh H - H \quad\mathrm{where}\quad H=iE
但从数学上讲, 这个式子其实就是:
M = i \left( E - \epsilon \sin E \right)
也就是说不考虑物理意义其实是一样的.
开普勒方程的解析解
有了方程当然接下来就是求解了咯, 古代计算力比较值钱, 毕竟没有计算机, 所以大家对解析解都有一种病态的追求.
怎么着推一天公式要比算一整天的牛顿迭代有趣吧?
\left\{\begin{aligned} \frac{\pi}{2}&=x-\sin x\\ \frac{\pi}{2}&=x-\frac{\pi}{180}\sin x \end{aligned}\right.
作一下等价性检验:
In [] = FindRoot[x==Cos@x,{x,0}]
x-Pi/2/.FindRoot[Pi/2==x-Sin@x,{x,1}]
FindRoot[x==Cos[Pi x/180],{x,0}]
180x/Pi-90/.FindRoot[Pi/2==x-Pi Sin@x/180,{x,1}]
Out[] = 0.7390851332151605`
{x -> 0.7390851332151607`}
0.9998477415310987`
{x -> 0.9998477415310881`}
拉格朗日反演
E不能分离但M, 展开M(E),然后直接用级数反演即可.
M(E) = (1-\epsilon)E+\epsilon\sum _{n=1}^{\infty } \frac{(-1)^n}{(2 n+1)!}E^{2 n+1}
\bigstar E(M)= \begin{cases} \displaystyle \sum _{n=1}^{\infty }\bigg(\lim_{\theta \to 0^{+}}\!{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}{\bigg (}{\frac {\theta }{\sqrt[{3}]{\theta -\sin(\theta )}}}{\bigg )}^{\!\!\!n}{\bigg )}{\frac {M^{\frac{n}{3}}}{n!}}&\epsilon=1\\ \displaystyle \sum_{n=1}^{\infty }\bigg(\lim_{\theta \to 0^{+}}{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}{\Big (}{\frac {\theta }{\theta -\epsilon\sin(\theta )}}{\Big )}^{\!n}{\bigg )}{\frac {M^{n}}{n!}}&\epsilon\neq 1 \end{cases}
Mathematica 可以很方便的执行级数反演.
Series[M- Sin[M], {M, 0, 10}]//InverseSeries
Series[M-e Sin[M], {M, 0, 10}]//InverseSeries
早期解这个方程使用了关于离心率\epsilon的麦克劳林展开.
E(M)=M+\sum_{n=1}^\infty a_n \epsilon^n;\ \epsilon\leq\mathrm{L}
这不是个整函数, 所以引入了所谓的拉普拉斯极限.
L=\max_{x\in\mathbb{R}}\frac{x}{\cosh (x)}\approx0.662743
超出收敛域的部分级数失效, 级数反演则很好的解决了这个问题.
贝塞尔函数解
当然无穷级数不利于计算, 能否使用微积分表达是我们接下来的探索重点.
我们来考虑函数方程:g (M) = E (M) - M
我们假设它可以展开为傅里叶级数, 分析原函数方程性态可以期望这是个正弦级数.
g (M) = \sum_{n = 1}^{\infty}a_n\sin (n M)
那么系数可以表达为:
a_n = \frac {2}{\pi}\int_0^\pi g(M) \sin(nM)\,\mathrm{d}M
我们来尝试计算, 嗯? 没思路怎么办...
无脑分部积分展开到能搞定为止呗.
\begin{aligned} a_n&=\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}g(M) -\frac{2}{\pi}\left[g(M)\frac{\cos(nM)}{n}\right]_0^\pi\\ &=\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}(E-M)\\ &=\frac{2}{\pi n}\int_0^\pi \cos[n(E-\epsilon\sin E)]\,\mathrm{d}E -\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}M\\ &=\frac{2}{\pi n}\int_0^\pi \cos(nE-n\epsilon\sin E)\,\mathrm{d}E \end{aligned}
而这正好是贝塞尔函数的定义式之一:
Bessel Function of the First Kind:J_n(z)=\frac{1}{\pi}\int_0^\pi \cos(n θ-z \sin θ)\,\mathrm{d}θ\ ;n\in \mathbb{Z}
于是原式可以写成
\bigstar E(M)=M+\sum _{n=1}^{\infty } \frac{2}{n}J_n(n \epsilon )\sin(nM)
赫维茨-勒奇超越函数解
Stack Exchange上有个用反三角函数和三角函数表示的解析解, 这个解比较有难度.
\mathcal{D}=\frac1\pi \int_0^{\pi } \arctan\left(\tan \left(\frac{t-\sin t+\frac{\pi }{2}}2\right)\right) \,\mathrm{d}t+\frac{1}{\pi }
特殊函数论中将以下级数称为赫维茨-勒奇超越函数(Lerch Transcendent Function)
\Phi (z,t,h):=\sum _{n=0}^{\infty } \frac{z^n}{(h+n)^t}
我们从上面的贝塞尔函数解开始, 还原掉贝塞尔函数:
E=M+\sum _{n=1}^{\infty } \frac{2}{n}\left[\frac{1}{\pi}\int_0^\pi \cos(n θ-n\epsilon \sin θ)\,\mathrm{d}θ\right]\sin(nM)
然后交换积分求和顺序.
E=M+\frac{2}{\pi}\int_0^\pi\left[\sum _{n=1}^{\infty } \frac{\sin(nM)}{n} \cos(n θ-n\epsilon \sin θ)\right]\,\mathrm{d}θ
里面的部分圈起来叫F(M), 用欧拉公式展开.\begin{aligned} F(M)=&\frac{\sin(nM)}{n} \cos(n θ-n\epsilon \sin θ)\\ =&\frac{i}{4 n}\left(e^{-i M n}-e^{i M n}\right) \left(e^{-i (\theta n-n \epsilon \sin (\theta ))}+e^{i (\theta n-n \epsilon \sin (\theta ))}\right)\\ =&\frac{i}{4 n}\left(e_1+e_2+e_3+e_4\right) \end{aligned}
其中:
\begin{cases} e_1=+\exp(-i M n+i \theta n-i n \epsilon \sin (\theta ))\\ e_2=-\exp(i M n+i \theta n-i n \epsilon \sin (\theta ))\\ e_3=+\exp(-i M n-i \theta n+i n \epsilon \sin (\theta ))\\ e_4=-\exp(i M n-i \theta n+i n \epsilon \sin (\theta ))\\ \end{cases}
可以发现其实都是e^{n\alpha}的结构.
我们引入多对数函数:
\mathrm{Li}_s(z) := z\Phi (z,s,1)=\sum _{n=1}^{\infty } \frac{z^n}{n^s}
也就是说:
\sum _{n=1}^{\infty } \frac{e^{a n}}{n}=\text{Li}_1\left(e^a\right)=i\arg (1-e^a)-\ln |1-e^a|
用这个函数化简等式:
\begin{aligned} E=&M+\frac{2}{\pi}\int_0^\pi\left[\sum _{n=1}^{\infty } \frac{i}{4 n}\left(e_1+e_2+e_3+e_4\right)\right]\,\mathrm{d}θ\\ =&M+\frac{i}{2\pi}\int_0^\pi\left[\text{Li}_1(e^{a_1})+\text{Li}_1(e^{a_2})+\text{Li}_1(e^{a_3})+\text{Li}_1(e^{a_4})\right]\,\mathrm{d}θ \end{aligned}
同样的整理一下:
\begin{cases} a_1=+i (\theta -M-\epsilon \sin (\theta ))\\ a_2=+i (\theta +M-\epsilon \sin (\theta ))\\ a_3=-i (\theta +M-\epsilon \sin (\theta ))\\ a_4=-i (\theta -M-\epsilon \sin (\theta ))\\ \end{cases}
可以合并成两组, 然后再次展开, 运算量有点大.
化简的时候注意恒等式:\arg(e^{ix})=\arctan(\tan (x)).
\begin{aligned} \sum \text{Li}_1(e^{a}) =&\frac{2}{i}\arctan\tan \left(\frac{\theta -M-\epsilon \sin (\theta )+\pi}{2} \right)\\ +&\frac{2}{i}\arctan\tan \left(\frac{-\theta -M+\epsilon \sin (\theta )+\pi}{2}\right) \end{aligned}
注意到第二部分:
\int_0^{\pi } \arctan\cot \left(\frac{1}{2} (\theta +M-\epsilon \sin (\theta ))\right) \, \mathrm{d}\theta =\epsilon+\frac{1}{4} \left( +\pi ^2-2 \pi M\right)
最后代回去大功告成!
\begin{aligned} \bigstar E=&M+\frac{i}{2\pi}\int_0^\pi\sum \text{Li}_1(e^{a})\,\mathrm{d}θ\\ =&\frac{1}{4} (2 M+\pi )+\frac{\epsilon }{\pi }+\frac{1}{\pi }\int_0^\pi\arctan\tan \left(\frac{\theta -M-\epsilon \sin (\theta )+\pi}{2} \right)\mathrm{d}\theta \end{aligned}
代入数据就得到了 Stack Exchange 一样的结果.
我对\arctan(\tan (x))这种写法感到很不爽.
这个当然不能直接抵消, 由于\arctan(\tan (x)) \neq x, 我们作复展开.
\begin{aligned} \arctan(\tan (x)) &=\frac{1}{2} i \log \left(1+\frac{e^{-i x}-e^{i x}}{e^{-i x}+e^{i x}}\right)-\frac{1}{2} i \log \left(1-\frac{e^{-i x}-e^{i x}}{e^{-i x}+e^{i x}}\right)\\ &=\frac{i}{2}\log \left(\frac{2}{1+e^{2 i x}}\biggl/\frac{2 e^{2 i x}}{1+e^{2 i x}}\right)\\ &=\frac{i}{2}\log (e^{-2 i x}) \end{aligned}
严格来说这两者不是完全相等的, 因为这样一来消掉了奇点.
不过积分的时候完全可以划等号, 因为区间开闭完全不影响积分值.
\bigstar E=\frac{1}{4} (2 M+\pi )+\frac{\epsilon }{\pi }+\frac{i}{2\pi }\int_0^\pi \log \left(-e^{i (M+\epsilon \sin\theta-\theta)}\right)\mathrm{d}\theta
综上所述, 最后代入值, 我们得到了:
\begin{aligned} \mathcal{D}_{\;}=&\frac{1}{\pi }\left[1+\frac{i}{2}\int_0^{\pi}\log \left(-i e^{i (\sin t-t)}\right)\;\mathrm{d}t\right]\\ \mathcal{D}_°=&\frac{1}{\pi }\left[1+\frac{90i}{\pi}\int_0^{\pi}\log \left(-i e^{i (\pi\sin t/180-t)}\right)\;\mathrm{d}t\right] \end{aligned}
(*真男人从不回头看数值验证*)
(2 + I Integrate[Log[-I/E^(I*(t - Sin[t]))], {t, 0, Pi}])/(2*Pi)//N
(Pi + 90I Integrate[Log[(-I)*E^((-I)*t + (1/180)*I*Pi*Sin[t])], {t, 0, Pi}])/Pi^2//N
> 0.7390851332151609`
> 0.9998477415310951`
只有娘们才喜欢用特殊函数
最后一个是百度贴吧上的, 这个答案就非常魔幻了,它和上面两个方法不是一个系列的, 和第一个方法有关.
暴力求解拉格朗日反演的解析形式, 场面非常的少儿不宜...
我一时半会儿也没看懂,详情看参考书目(3).
\begin{aligned} \mathcal{D}=&\frac{1}{2} \pi \exp \left(\int_0^1 {\frac{1}{\pi x}\arctan\left(\frac{x \log \left(\frac{\sqrt{1-x^2}+1}{x}\right)(\pi x+2) }{x^2 \log ^2\left(\frac{\sqrt{1-x^2}+1}{x}\right)-\pi x-1}\right) \, \mathrm{d}x}\right)\\ =&\mathrm{arccot}\left(1+\frac{1}{2 \pi }\int_0^1{ \log \left(\frac{\pi ^2 \left(1-x^2\right)+4 \left(\sqrt{1-x^2} \mathrm{arctanh}(x)+x\right)^2}{\pi ^2 \left(1-x^2\right)+4 \left(\sqrt{1-x^2} \mathrm{arctanh}(x)-x\right)^2}\right) \, \mathrm{d}x}\right) \end{aligned}
从这个结果上也能看出这个方法有多残暴...
(*怎么可以这么暴力的说*)
\[Pi]/2 Exp[NIntegrate[1/(\[Pi] x) ArcTan[((\[Pi] x+2)Log[(Sqrt[1-x^2]+1)/x]x)/(x^2Log[(Sqrt[1-x^2]+1)/x]^2-\[Pi] x-1)],{x,0,1},WorkingPrecision->50]]
ArcCot[1+1/(2\[Pi] ) NIntegrate[Log[((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]+x)^2)/((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]-x)^2)],{x,0,1},WorkingPrecision->50]]
> 0.73908513321516064165531208767387340401341175890075746496567242428255184768807`50.12267193056545
> 0.73908513321516064165531208767387340401341175890075746496567993239614795659229`51.22422170141253
参考书目
On Taylor series and Kapteyn series of the first and second type
Kepler's equation, radiation problems and Meissel's expansion
An exact analytical solution of Kepler's Equation
Zeta(2) 有图版
我很早就一直想写一篇文章,跟大家聊一聊:
本文假设读者热爱数学,并且曾经掌握过高中数学知识。
1. 首先我们要复习一下三角函数。
对于任意的角 x, 我们有 {\sin^2 x}+\cos^2x=1,这跟勾股定理是一回事。
接下来是一个重要的公式,建议读者通过画图理解

然后通过画出三角函数图像的方式,我们还可以轻易验证如下两条公式
2. 现在我们可以开始证明了。
(该证明取自美国数学月刊2002年2月第109期 pp. 196-200 作者系Josef Hofbauer。)
2.1
由于 \sin(2x) = 2 \sin x \cos x,所以
根据定义可知
现在,利用恒等式 \sin(π-x)=\sin x,可得
2.2
有读者可能要问,为什么要像刚才那样做,其实原因马上就很清楚了,目的只有一个:让所有 \sin()里的值都是锐角。
因为对于锐角x,我们有 \sin x < x < \tan x

取倒数,平方,得
(各位读者请注意,刚才这三个不等关系(3)(4)(5)可能需要花时间仔细读懂。尤其是(3),是全文中最难理解的一步,希望读者能耐心地读懂:如何可以从之前的公式(1)(2)推导出(3)?)
2.3
通过观察,我们可以发现,之前在(**)中,我们只用到
则有
2.4
现在我们离结论只有一步之遥,
令
证明完毕!
怎么样,好玩吧,数学永远是这样,用最巧妙的逻辑链条构造最美丽的证明。
只要有一点点好奇心,和足够的耐心,人人都可以享受数学的乐趣。
祝大家暑假愉快。
贾博名
2014年6月20日 于 美国俄亥俄州哥伦布市
(最新一次更新于2016年6月19日,再次感谢孙豪同学对本文初稿的认真阅读,并指出了多处笔误,现已更正。)
我很早就一直想写一篇文章,跟大家聊一聊:
本文假设读者热爱数学,并且曾经掌握过高中数学知识。
1. 首先我们要复习一下三角函数。
对于任意的角 x, 我们有 {\sin^2 x}+\cos^2x=1,这跟勾股定理是一回事。
接下来是一个重要的公式,建议读者通过画图理解

然后通过画出三角函数图像的方式,我们还可以轻易验证如下两条公式
2. 现在我们可以开始证明了。
(该证明取自美国数学月刊2002年2月第109期 pp. 196-200 作者系Josef Hofbauer。)
2.1
由于 \sin(2x) = 2 \sin x \cos x,所以
根据定义可知
现在,利用恒等式 \sin(π-x)=\sin x,可得
2.2
有读者可能要问,为什么要像刚才那样做,其实原因马上就很清楚了,目的只有一个:让所有 \sin()里的值都是锐角。
因为对于锐角x,我们有 \sin x < x < \tan x

取倒数,平方,得
(各位读者请注意,刚才这三个不等关系(3)(4)(5)可能需要花时间仔细读懂。尤其是(3),是全文中最难理解的一步,希望读者能耐心地读懂:如何可以从之前的公式(1)(2)推导出(3)?)
2.3
通过观察,我们可以发现,之前在(**)中,我们只用到
则有
2.4
现在我们离结论只有一步之遥,
令
证明完毕!
怎么样,好玩吧,数学永远是这样,用最巧妙的逻辑链条构造最美丽的证明。
只要有一点点好奇心,和足够的耐心,人人都可以享受数学的乐趣。
祝大家暑假愉快。
贾博名
2014年6月20日 于 美国俄亥俄州哥伦布市
(最新一次更新于2016年6月19日,再次感谢孙豪同学对本文初稿的认真阅读,并指出了多处笔误,现已更正。)