作者:沉默中的思索
链接:https://www.zhihu.com/question/22298352/answer/219141654
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
假设现在有一个序列:

现在要对这个序列进行变换,将这个序列的每个元素和它相邻的两个元素做平均得到新序列上对应的值,比如4对应到新序列上的值就是 ,2对应到新序列上的值就是
,依次类推就得到一个新序列,这个过程其实就是移动平均。
上面的变换也可以看成用一个长度为3,每个元素为1/3的小窗,在初始的序列上不断移动并对应相乘再相加的过程。

但是有的人可能觉得这个过程不太完美,认为转换的过程中使用移动平均不能完美的表达上述转换。因为转换的过程中中间的那个元素对新序列上的值权重比较大,他的两个邻居权重应该小点。这时候我们修改那个长度为3的小窗口,将其变成下面的样子:
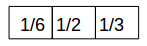
但是每个小框权重是多少我们不好确定,干脆不如直接将其表示成函数得了,也不纠结它是多少了,于是就有了下面的函数:
假设我们的序列也是一个函数: ,则上述变换过程就可以变成数学公式:
对于序列 上的任意元素
的变换过程都可以表示成:
其实这就是cross—correlation的定义式,跟卷积已经差不多了。如果我们每次在上述转换前先将小框倒置一下再去对应相乘再相加,也就是说将1/6,1/2,1/3的小框先变成1/3,1/2,1/6再去做变换我们就会得到卷积的公式 。
上面是离散的情况下卷积的公式,如果我们的小框长度不是3而是无限长,而且小框里的元素都是连续的,这时候我们就得到真正意义上的卷积公式:
对于二维情况下的卷积同理。
从信号的角度理解:也可以这么理解,对于一个信号,你要计算t=4时刻其影响,但是t=0,1,2,3时刻的影响也对t=4有影响,只是在t=4时,它们的影响已经比较小了,所以也要考虑它们的影响不过要把它们的影响赋予一个小的权重