推荐一篇很好的博客:http://www.cppblog.com/menjitianya/archive/2015/11/02/212171.html
一、树状数组的定义
基本定义:树状数组是利用二分的思想使得查询和修改的复杂度都为 log(n) 的数据结构,树状数组是通过前缀和思想,用来完成单点更新和区间查询的数据结构。
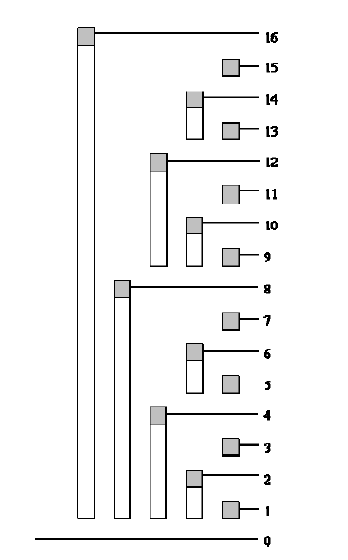
如上图,不难看出树状数组是一个不断地二分的过程。
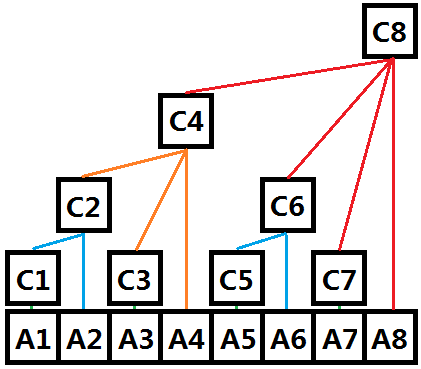
如上图,其中A为普通数组,C为树状数组(C在物理空间上和A一样都是连续存储的)。树状数组的第4个元素C4的父结点为C8 (4的二进制表示为"100",所以k=2,那么4 + 2^2 = 8,下面会具体讲解树状数组节点的含义),C6和C7同理。C2和C3的父结点为C4,同样也是可以用上面的关系得出的,那么从定义出发,奇数下标一定是叶子结点。
谈到树状数组就很有必要谈一下线段树,下图就是一个线段树:

于是删除了线段树的所有右儿子,发现就形成了树状数组。与线段树相比,所用空间更小,速度更快,而且编程的复杂难度也大大减小。但是这里有一个前提条件,也是树状数组的缺陷:节点的数据必须是可加减,而且要满足a + b = c,c - a = b,比如集合运算,是不能通过父节点和左子节点 来计算右子节点的。
和ST相比,树状数组可以动态更新数据。

二、结点的含义

这时就要说到树状数组的一个很重要操作:lowbit(x),返回参数转为二进制后,最后一个1的位置所代表的数值。计算方法:
int lowbit(int x) {
return x & (-x);
}现在来看树状数组上的结点Ci具体表示什么,我们定义Ci的值为它的所有子结点的值 和 Ai 的总和,之前提到当i为奇数时Ci一定为叶子结点,所以有Ci = Ai ( i为奇数 )。从图中可以得出:
C1 = A1
C2 = C1 + A2 = A1 + A2
C3 = A3
C4 = C2 + C3 + A4 = A1 + A2 + A3 + A4
C5 = A5
C6 = C5 + A6 = A5 + A6
C7 = A7
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
建议直接看C8,因为它最具代表性。
我们从中可以发现,其实Ci还有一种更加普适的定义,它表示的其实是一段原数组A的连续区间和。根据定义,右区间是很明显的,一定是i,即Ci表示的区间的最后一个元素一定是Ai,那么接下来就是要求Ci表示的第一个元素是什么。从图上可以很容易的清楚,其实就是顺着Ci的最左儿子一直找直到找到叶子结点,那个叶子结点就是Ci表示区间的第一个元素。
更加具体的,如果i的二进制表示为1000,那么它最左边的儿子就是 0100,这一步是通过结点父子关系的定义进行逆推得到,并且这条路径可以表示如下:
1000 => 0100 => 0010 => 0001
这时候,0001已经是叶子结点了,所以它就是 Ci 能够表示的第一个元素的下标,那么我们发现,如果用 k 来表示 i 的二进制末尾0的个数,Ci能够表示的A数组的区间的元素个数为 2^k,又因为区间和的最后一个数一定是Ai,所以有如下公式:
Ci = sum{ A[j] | i - 2^k + 1 <= j <= i } (帮助理解:将 j 的两个端点相减+1 等于2^k)
所以,树状数组中一定不能有0元,如果题目中有要注意处理。通常是整体数据加1,这样后同时也要注意变化后的数据上限
三、更新操作
更新操作就是之前提到的add(i, x) 和 add(i, -x),也就是单点的加减操作。
那么其实就是求在Ai改变的时候会影响哪些Ci,看上面树形结构Ai的改变只会影响Ci及其祖先结点,即A5的改变影响的是C5、C6、C8,而A1的改变影响的是C1、C2、C4、C8。也就是每次add(i, x),我们只需要更新Ci以及它的祖先结点。
int add(int p, int x) {
for(int i = p; i <= n; i += lowbit(i)) presum[i] += x;
}
四、求和操作
求区间 [l, r] 的和时,只需要利用树状数组求出 [1, r] 的前缀和再减去 [1, l] 的前缀和即可。
int sum(int x){
int ans =0;
for(int i = x; i > 0; i -= lowbit(i)) ans += presum[i];
return ans;
}五、小结
树状数组的本质上是单点修改,区间查询。树状数组的c[i]保存的是它所属的下属元素的累加和,每次查询区间的时候都是从1到x这个区间里面的所有元素的和,每次在更新的时候也是不断的将控制它的c[i]也更新。
六、树状数组的经典模型
1、点更新,段求和
【例题1】一个长度为n(n <= 500000)的元素序列,一开始都为0,现给出三种操作:
1. add x v : 给第x个元素的值加上v; ( a[x] += v )
2. sub x v : 给第x个元素的值减去v; ( a[x] -= v )
3. sum x y: 询问第x到第y个元素的和; ( print sum{ a[i] | x <= i <= y } )
这是树状数组最基础的模型,1和2的操作就是对应的单点更新,3的操作就对应了前缀求和。1和2只要分别调用 add(x, v) 和 add(x, -v),而3则是输出 sum(y) - sum(x-1) 的值。
2、段更新,点求值
【例题2】一个长度为n(n <= 500000)的元素序列,一开始都为0,现给出两种操作:
1. add l, r, x : 给第 l 个元素到第 r 个元素的值都加上 x( a[i] += x, 其中 l <= i <= r )
2. get x: 询问第x个元素的值(print a[x] )
这类问题对树状数组稍微进行了一个转化,对于操作1我们只需要执行两个操作,即 add(l, x) 和 add(y+1, -v),而操作2则是输出sum(x)的值。这样就把区间更新转化成了单点更新,单点求值转化成了区间求和。
3、逆序模型
【例题3】给定一个长度为n(n <= 500000)的排列a[i],求它的逆序对对数。1 5 2 4 3 的逆序对为(5,2)(5,3)(5,4)(4,3),所以答案为4。
朴素算法,枚举任意两个数,判断他们的大小关系进行统计,时间复杂度O(n^2)。
来看一个给定n个元素的排列 X0, X1, X2……Xn,其中第 i 个元素 Xi,如果想知道以他为首的逆序对的数目(形如(Xi, Xj)这样的数对),就是需要计算Xi+1, ……, Xn 这个序列中小于 Xi 的元素个数。那么我们只需要对这个排列从后往前枚举,每次枚举到 Xi 元素时,执行 ans += sum(Xi - 1),然后再执行add(Xi, 1),n个元素枚举完毕,得到的 ans 就是我们要求的逆序数了。总的时间复杂度O(nlogn)。
这个模型和之前的区别在于它不是将原数组的下标作为树状数组的下标,而是将元素本身作为树状数组的下标。
这里就需要引入另一道求逆序对的题了:
【例题4】POJ 2299 Ultra-QuickSort
与这道不同的是数组元素最大值可以达到 999,999,999,那么也就无法将元素本身作为树状数组的下标,这时就需要利用离散化思想,由于最多只有 500000 个数,可以把原始的数映射为1-n一共n个数,具体请看另一篇博客:https://blog.csdn.net/Jasmineaha/article/details/81449834。
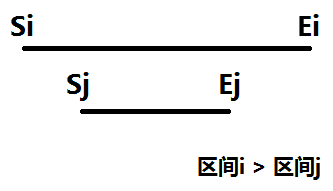
【例题5】给定N(N <= 100000)个区间,定义两个区间 (Si, Ei) 和 (Sj, Ej) 的 '>' 规定如下:
如果Si <= Sj 并且 Ej <= Ei 并且 Ei - Si > Ej - Sj,则 (Si, Ei) > (Sj, Ej),现在要求每个区间有多少区间 '>' 它
将上述三个关系式化简,可以得到 区间 i > 区间 j 的条件是:区间 i 完全覆盖 区间 j,并且两者不相等。
首先对区间进行排序,排序规则为:按区间的右端点从大到小排序,如果右端点相同,则左端点小的排在前面
那么当读取到第 i 个牛的 Si 和 Ei时,之前(假设任意两个区间不会完全相同)的牛的 Sj(j<=i-1) <= Si 的这些牛就都比 i 号牛强壮了。枚举区间,不断插入区间左端点,因为区间右端点是保持递减的,所以对于某个区间(Si, Ei),只需要查询树状数组中 [1, Si] 这一段有多少已经插入的数据,就能知道有多少个区间是比它大的,这里需要注意的是多个区间相等的情况,因为有排序,所以它们在排序后的数组中一定是相邻的,所以在遇到有相等区间的情况时,当前的区间的答案就等于上一个相等的区间的答案。
这里的插入即 add(Sj, 1),统计则是 sum(Si) (其中j < i)。
参考博客:https://blog.csdn.net/Jasmineaha/article/details/81474680
4、二分模型