恩,这是AC的第一道树状数组呢。
本蒟蒻以前遇到RMQ问题一般都用线段树或ST表,可惜ST表不支持在线修改,而线段树代码量又太大。
如今终于找到了折中方案:树状数组!!!!
代码量小,还支持修改!
树状数组也就是二叉索引树,又被称为Fenwick树,然而我个人认为它不能被严谨地成为树,因为充其量只是借用的树形结构的思想,于实现上有着较大的区别。
树状数组虽然运用范围没有线段树那么广,但是它的效率要高很多,比如线段树是nlogn,但树状数组是logn。
还有一点需要注意的是:树状数组可以区间查询,但不能运用于任意区间查询。这一点在后面会提到。
那么这个树状数组的基本思路就是
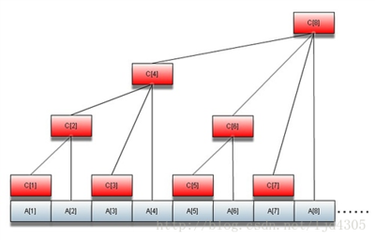
用节点ci储存和,比如:
- c1=a1
- c2=a1+a2
- c3=a3
- c4=a1+a2+a3+a4
- c5=a5
- c6=a5+a6
- c7=a7
- c8=a1+...+a8
当然这样子可能不是很容易看出内在的联系,因此不妨将其转化为二进制来观察:
- c0001=a0001
- c0010=a0001+a0010
- c0011=a0011
- c0100=a0001+a0010+a0011+a0100
- c0101=a0101
- c0110=a0101+a0110
- c0111=a0111
- c1000=a0001+...+a1000
是不是发现了什么?
没有吗?好吧。
事实上这里的规律就是cn=a(n–2^k+1)+...+an,这里的k指的是n二进制末尾0的数量。
获取2^k的操作我们称之为lowbit,其实现如下:
int lowbit(int k){ return k&(-k); }
有了lowbit操作之后,求和就很好写了:
1 int query(int x){ 2 int ans=0; 3 while(x!=0){ 4 ans+=tree[x]; 5 x-=lowbit(x); 6 } 7 return ans; 8 }
要注意一点,这里求的ans是区间[1,x]的和,想要[y,x]的和只能query(x)-query(y-1)。
因此我们回到了之前那个问题:树状数组不能解决所有区间查询,**它只能解决如上的有关联的区间查询。**
emmmm.....还有update操作:
1 void update(int x,int k){ 2 while(x<=n){ 3 tree[x]+=k; 4 x+=lowbit(x); 5 } 6 }
这个在明白了树状数组的本质之后也很好理解,就不多做叙述了。
总的来说,树状数组挺好用的,值得一学。但切记,无论如何都必须掌握线段树,因为能用树状数组解决的都能用线段树,而反之不一定如此。
另附AC代码见下:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 6 const int maxn=500500; 7 8 int n,m; 9 int tree[maxn<<2]; 10 11 int lowbit(int k){ 12 return k&(-k); 13 } 14 15 void update(int x,int k){ 16 while(x<=n){ 17 tree[x]+=k; 18 x+=lowbit(x); 19 } 20 } 21 22 int query(int x){ 23 int ans=0; 24 while(x!=0){ 25 ans+=tree[x]; 26 x-=lowbit(x); 27 } 28 return ans; 29 } 30 31 int main(){ 32 scanf("%d%d",&n,&m); 33 for(int i=1;i<=n;i++){ 34 int a; 35 scanf("%d",&a); 36 update(i,a); 37 } 38 for(int i=1;i<=m;i++){ 39 int a,b,c; 40 scanf("%d%d%d",&a,&b,&c); 41 if(a==1)update(b,c); 42 else printf("%d\n",query(c)-query(b-1)); 43 } 44 }
恩,这是AC的第一道树状数组呢。
本蒟蒻以前遇到RMQ问题一般都用线段树或ST表,可惜ST表不支持在线修改,而线段树代码量又太大。。
如今终于找到了折中方案:**树状数组!!!!**###### 代码量小,还支持修改!
------------
**树状数组**也就是**二叉索引树**,又被称为**Fenwick树**,然而我个人认为它不能被严谨地成为树,因为充其量只是借用的树形结构的思想,于实现上有着较大的区别。
树状数组虽然运用范围没有线段树那么广,但是它的效率要高很多,比如线段树是nlogn,但树状数组是logn。
还有一点需要注意的是:树状数组可以区间查询,但不能运用于任意区间查询。这一点在后面会提到。
------------
那么这个树状数组的基本思路就是

用节点ci储存和,比如:
- c1=a1- c2=a1+a2- c3=a3- c4=a1+a2+a3+a4- c5=a5- c6=a5+a6- c7=a7- c8=a1+...+a8
当然这样子可能不是很容易看出内在的联系,因此不妨将其转化为二进制来观察:
- c0001=a0001- c0010=a0001+a0010- c0011=a0011- c0100=a0001+a0010+a0011+a0100- c0101=a0101- c0110=a0101+a0110- c0111=a0111- c1000=a0001+...+a1000
是不是发现了什么?
没有吗?好吧。
事实上这里的规律就是**cn=a(n–2^k+1)+...+an**,这里的k指的是**n二进制末尾0的数量**。
获取2^k的操作我们称之为lowbit,其实现如下:
```cppint lowbit(int k){return k&(-k);}```
有了lowbit操作之后,求和就很好写了:
```cppint query(int x){int ans=0;while(x!=0){ans+=tree[x];x-=lowbit(x);}return ans;}```
要注意一点,这里求的ans是区间[1,x]的和,想要[y,x]的和只能query(x)-query(y-1)。
因此我们回到了之前那个问题:树状数组不能解决所有区间查询,**它只能解决如上的有关联的区间查询。**
emmmm.....还有update操作:
```cppvoid update(int x,int k){while(x<=n){tree[x]+=k;x+=lowbit(x);}}```
这个在明白了树状数组的本质之后也很好理解,就不多做叙述了。
------------
总的来说,树状数组挺好用的,值得一学。但切记,**无论如何都必须掌握线段树**,因为能用树状数组解决的都能用线段树,而反之不一定如此。
另附AC代码见下:
```cpp#include<iostream>#include<cstdio>#include<algorithm>using namespace std;
const int maxn=500500;
int n,m;int tree[maxn<<2];
int lowbit(int k){return k&(-k);}
void update(int x,int k){while(x<=n){tree[x]+=k;x+=lowbit(x);}}
int query(int x){int ans=0;while(x!=0){ans+=tree[x];x-=lowbit(x);}return ans;}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){int a;scanf("%d",&a);update(i,a);}for(int i=1;i<=m;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);if(a==1)update(b,c);else printf("%d\n",query(c)-query(b-1));}}```