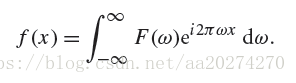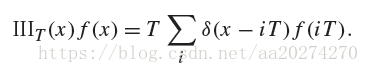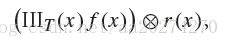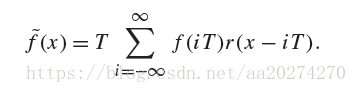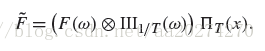概述
1. Although the final output of a renderer like pbrt is a two-dimensional grid of colored
pixels, incident radiance is actually a continuous function defined over the film plane.
The manner in which the discrete pixel values are computed from this continuous function
can noticeably affect the quality of the final image generated by the renderer; if this
process is not performed carefully, artifacts will be present. Fortunately, a relatively small
amount of additional computation to this end can substantially improve the quality of
the rendered images.
(整个 Film Plane 上的 incident radiance 实际上是一个连续函数 ,但是Pixel是离散的,这些离散的Pixel其实是从incident radiance 连续函数中计算出来, 其实个人理解,就是利用 离散的Pixel去重新构建一个新的函数,逼近 原来的连续函数)
2. sampling theory—the theory of taking discrete sample values
from functions defined over continuous domains and then using those samples to reconstruct
new functions that are similar to the original.Building on principles of sampling
theory, the Samplers in this chapter select sample points on the image plane at which incident
radiance will be computed
(采样的理论就是,从一个连续函数A中进行采样,得到一些采样点,利用这些采样点,重新构造出一个新的函数B,使得函数B 相似于 原来的函数A)
Sampling Theory
1. When thinking about digital images, it is important to differentiate between image pixels, which represent the value of a
function at a particular sample location, and display pixels, which are physical objects that emit light with some distribution.
(Pixel 表示的就是 采样一个函数的某一个位置得到的函数值)
2.
Displays use the image pixel values to construct a new image function over the display
surface.This function is defined at all points on the display, not just the infinitesimal
points of the digital image’s pixels. This process of taking a collection of sample values
and converting them back to a continuous function is called reconstruction.
(显示器 使用所有 Pixel 值来为整个屏幕构建一个新的图像函数,这个新的图像函数不只是和Pixel有关,还是和整个屏幕的所有的点都有关,这个收集采样值和把他们转成一个连续函数的过程叫做 reconstruction)
3.
In order to compute the discrete pixel values in the digital image, it is necessary to sample
the original continuously defined image function. In pbrt, like most other ray-tracing
renderers, the only way to get information about the image function is to sample it by
tracing rays.
(为了计算图片里面的离散像素值,需要去采样 原始的连续的图片函数,在pbrt中,或者其他的光线追踪渲染器,去获得图片函数信息的唯一方式就是 发射线去采样)
4.
While an image could be generated by just sampling the function precisely at the pixel positions, a
better result can be obtained by taking more samples at different positions and incorporating
this additional information about the image function into the final pixel values.
5.
Indeed, for the best-quality result, the pixel values should be computed such that the reconstructed
image on the display device is as close as possible to the original image of the
scene on the virtual camera’s film plane.
(最好的图片质量就是,用 Pixel 来 重构 的图片 尽可能地接近 真实相机拍出来的 相片)
6.
Because the sampling and reconstruction process involves approximation, it introduces
error known as aliasing, which can manifest itself in many ways, including jagged edges
or flickering in animations. These errors occur because the sampling process is not able
to capture all of the information from the continuously defined image function.
(走样主要是因为,采样的过程中没有 在连续的图片函数中 获得足够的信息)
7.
Because the only information available
about f comes from the sample values at the positions x‘, ˜ f is unlikely to match f
perfectly since there is no information about f ’s behavior between the samples.
(上面演示的就是,在 原函数 进行采样,利用采样点 重构 一个新的函数出来)
8.
Fourier analysis can be used to evaluate the quality of the match between the reconstructed
function and the original.
(简单理解:傅里叶分析 是用来评估 重构函数和原函数 的差别大不大)
The Frequency Domain And The Fourier Transform
1.
One of the foundations of Fourier analysis is the Fourier transform, which represents a
function in the frequency domain. (We will say that functions are normally expressed in
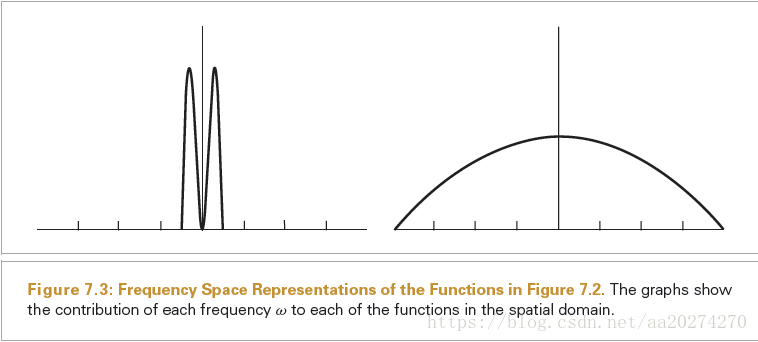
the spatial domain.) Consider the two functions graphed in Figure 7.2. The function in
Figure 7.2(a) varies relatively slowly as a function of x, while the function in Figure 7.2(b)
varies much more rapidly. The slower-varying function is said to have lower frequency
content. Figure 7.3 shows the frequency space representations of these two functions;
the lower-frequency function’s representation goes to zero more quickly than the higherfrequency
function.
(Fourier transform 可以用 把一个 函数从 spatial domain 变到 frequency domain)
Most functions can be decomposed into a weighted sum of shifted sinusoids. This remarkable
fact was first described by Joseph Fourier, and the Fourier transform converts a
function into this representation. This frequency space representation of a function gives
insight into some of its characteristics—the distribution of frequencies in the sine functions
corresponds to the distribution of frequencies in the original function. Using this
form, it is possible to use Fourier analysis to gain insight into the error that is introduced
by the sampling and reconstruction process, and how to reduce the perceptual impact of
this error.
(Fourier transform 可以用 把一个 函数从 spatial domain 变到 frequency domain,在 frequency domain 中表示一个函数的话,可以更方便地看清楚这个函数的 一些特征,方便查错和纠错)
2.
The Fourier transform of a one-dimensional function f (x) is
The new function F is a function of frequency, ω。
We will denote the Fourier transform operator by 







3.
The inverse Fourier transform
Ideal Sampling And Reconstruction
1. (数学来表示采样)
Recall that the sampling process requires us to choose a set of equally spaced
sample positions and compute the function’s value at those positions. Formally, this corresponds
to multiplying the function by a “shah,” or “impulse train,” function, an infinite
sum of equally spaced delta functions. The shah 
where T defines the period, or sampling rate. This formal definition of sampling is
illustrated in Figure 7.4. The multiplication yields an infinite sequence of values of the
function at equally spaced points:
2. Reconstructed function
These sample values can be used to define a reconstructed function 
reconstruction filter function r(x) and computing the convolution
where the convolution operation ⊗ is defined as
For reconstruction, convolution gives a weighted sum of scaled instances of the reconstruction
filter centered at the sample points:
For example, in Figure 7.1, the triangle reconstruction filter, f (x) = max(0, 1− |x|), was
used. Figure 7.5 shows the scaled triangle functions used for that example.
We have gone through a process that may seem gratuitiously complex in order to end up at an intuitive result: the reconstructed function ~f(x) can be obtained by interpolating
among the samples in some manner. By setting up this background carefully, however,
Fourier analysis can now be applied to the process more easily.
3. Reconstructed function in frequency domain
An important idea used in Fourier analysis is the fact that the Fourier transform of the
product of two functions 
individual Fourier transforms F(ω) and G(ω):
It is similarly the case that convolution in the spatial domain is equivalent to multiplication
in the frequency domain:
These properties are derived in the standard references on Fourier analysis. Using these
ideas, the original sampling step in the spatial domain, where the product of the shah
function and the original function f (x) is found, can be equivalently described by the
convolution of F(ω) with another shah function in frequency space.
(如果把上面的 Reconstructed function in spatial domain 的最后一个公式套上去,其实就是说明,在 spatial domain 中的乘法可以用 frequency domain 空间的 卷积 代替)
We also know the spectrum of the shah function 
transform of a shah function with period T is another shah function with period 1/T .
This reciprocal relationship between periods is important to keep in mind: it means that
if the samples are farther apart in the spatial domain, they are closer together in the
frequency domain.
(如果 采样点 在 spatial domain 中是距离较远的话,那么在 frequency domain.距离就会比较紧凑)
Thus, the frequency domain representation of the sampled signal is given by the convolution
of F(ω) and this new shah function. Convolving a function with a delta function
just yields a copy of the function, so convolving with a shah function yields an infinite
sequence of copies of the original function, with spacing equal to the period of the shah
(Figure 7.6). This is the frequency space representation of the series of samples.
(根据上面所说的,在 frequency domain 中,Reconstructed 公式带有 卷积,例如 一个function 和 delta function 的卷积,得到的结果就是直接克隆 这个function,如果是 一个function 与 shah function 进行卷积,就是 无限的克隆这个function,看以下的图片)
Now that we have this infinite set of copies of the function’s spectrum, how do we
reconstruct the original function? Looking at Figure 7.6, the answer is obvious: just
discard all of the spectrum copies except the one centered at the origin, giving the original
F(ω). In order to throw away all but the center copy of the spectrum, we multiply by a
box function of the appropriate width (Figure 7.7). The box function 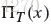
is defined as
(利用一个 Box Function 来 获得 reconstruct origin function)
This multiplication step corresponds to convolution with the reconstruction filter in the
spatial domain. This is the ideal sampling and reconstruction process. To summarize:
This is a remarkable result: we have been able to determine the exact frequency space
representation of f (x), purely by sampling it at a set of regularly spaced points. Other
than knowing that the function was band limited, no additional information about the
composition of the function was used.
4. Reconstructed function in spatial domain
Applying the equivalent process in the spatial domain will likewise recover f (x) exactly.
Because the inverse Fourier transform of the box function is the sinc function, ideal
reconstruction in the spatial domain is found by
or
Unfortunately, because the sinc function has infinite extent, it is necessary to use all of
the sample values f (i) to compute any particular value of ˜ f (x) in the spatial domain.
Filters with finite spatial extent are preferable for practical implementations even though
they don’t reconstruct the original function perfectly.
A commonly used alternative in graphics is to use the box function for reconstruction,
effectively averaging all of the sample values within some region around x. This is a very
poor choice, as can be seen by considering the box filter’s behavior in the frequency
domain: This technique attempts to isolate(隔绝) the central copy of the function’s spectrum
by multiplying by a sinc, which not only does a bad job of selecting the central copy of the
function’s spectrum but includes high-frequency contributions from the infinite series of
other copies of it as well.