概述
The idea here is to take a generally infinite-dimensional space of functions (pixel radiance
as a function of light-source position) and represent them with a specific set of basis
functions and corresponding basis function coefficients. Given a fixed preselected set
of basis functions, the coefficient values at each pixel define the approximation to the
general function in terms of the basis. The result will usually be an approximation, since
a finite set of coefficients can’t represent all possible functions. However, if the basis is
chosen well, or the functions being approximated have properties like smoothness that
can be taken advantage of, the results can be close enough for many applications.
(这里的思想是取一个无限大空间的函数,可以用一组特定的基来和相应的基函数系数 来表示它。)
A Piecewise-Constant Basis (Example)
A straightforward example of using basis functions to approximate an arbitrary function
is to use a set of piecewise-constant basis functions, where we might decide to use four
basis functions over the range [0, 1]. The first basis function, B1(x), has the value one
between zero and 1/4 and is zero elsewhere; the next one, B2(x), is one between 1/4 and
2/4; and so forth.
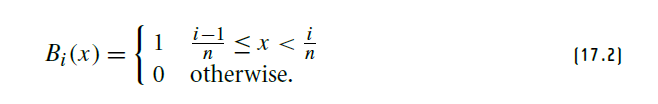
To represent an arbitrary function f (x) in this basis, we might evaluate it at a series
of positions at the midpoint of each basis function’s range, xi , x0 = 1/8, x1 = 3/8, and
so forth, giving a series of basis coefficient values ci = f (xi). The representation of
the original function in the basis, ˜ f (x), is then found by a weighted sum of the basis
functions (Figure 17.2):
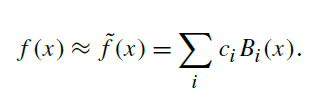

Figure 17.2: Representation of a Function in a Simple Piecewise-Constant Basis. A function
(dashed lines) represented in the basis function defined by Equation (17.2) (solid lines).
Projection Onto A Basis
In the general case, we are given some function f (x) and have selected a set of N basis
functions Bi(x) defined over a domain D. (Here we are using the notation f (x) to represent
more than just functions over the 1D reals, but instead functions over arbitrarydimensional
domains.) We then want to compute the coefficients ci that represent the
function in the basis. The approximated function is given by the weighted sum of basis
functions
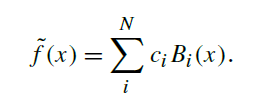
In particular, we would like a set of ci such that they minimize the difference between the
original function f (x) and the approximated function ˜ f (x).
It can be shown that the optimal coefficients in terms of minimizing the least-squares
error between f (x) and ˜ f (x) are given by integrating f (x) with the dual of the basis,
˜Bi(x):
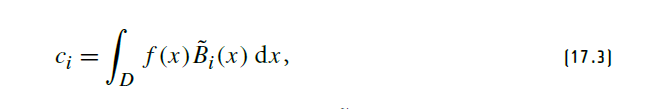
where the dual of a basis function is defined as the function ˜Bi(x) such that
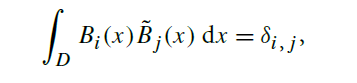
where δi , j is the Kronecker delta function,
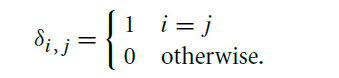
(上面的说明了,如果计算一个 ci, 这个ci 是 使原始函数f(x)和近似函数˜f(x)之间的差最小,其中,要用到
基函数的对偶函数:˜Bi (x))
Orthonormal Basis Functions
An important type of basis functions are orthonormal basis functions. An orthonormal
basis has two important properties. The first is orthogonality(正交): given any two distinct(不同) basis
functions Bi(x) and Bj (x) where i = j , the integral of the product of the two basis
functions is zero:
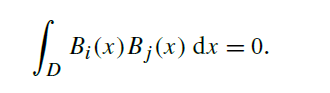
An important type of basis functions are orthonormal basis functions. An orthonormal
basis has two important properties. The first is orthogonality: given any two distinct basis
functions Bi(x) and Bj (x) where i = j , the integral of the product of the two basis
functions is zero:
The second property of an orthonormal basis is a normalization(标准化) property—the integral
of a particular basis function with itself over the domain is one:
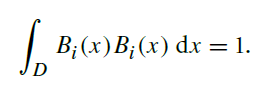
(orthonormal basis functions 有两个属性,一个是 orthogonality,一个是 normalization)
Using an orthonormal basis to represent a space of functions has two important advantages
compared to using a non-orthonormal basis: projecting a function into the basis is
easier, and integration of the product of functions in the basis can be computed extremely
efficiently.(使用标准正交基来表示函数空间有两个重要的优点)
The first advantage—easy projection of functions into the basis—comes from the useful
feature of orthonormal basis functions that each basis function is equal to its dual:
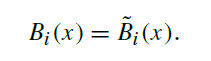
The effect of this property is that coefficients of an arbitrary function in the basis are
found by just integrating against the basis functions themselves:

There’s no need to find the dual basis functions for the chosen basis.
(第一个优点,每个基函数都等于它的对偶,所以,就可以直接利用基函数来求 ci)
The second advantage, efficient integration, is an extremely useful one in practice. We
will often want to compute the integral of the product of two functions represented in
the basis (for example, a BRDF function and an incident radiance function). If the two
functions f (x) and g(x) are represented by two sets of coefficients, ci and ci’ , in the basis,
the integral is
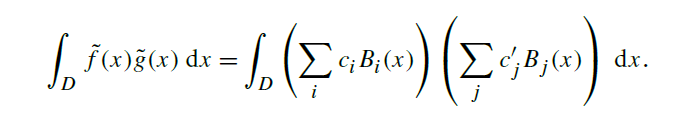
The sums and the coefficients can be pulled outside of the integral, giving a nested sum
of integrals of products of basis functions:
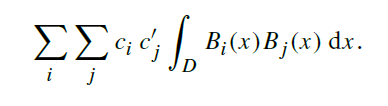
Recall that orthonormality means that for i != j ,

Therefore, many terms in the above sum are necessarily zero, and what remains is:

Finally, because the integral of the product of an orthonormal basis function with itself
is one, the integrals are all one, and we are left with:
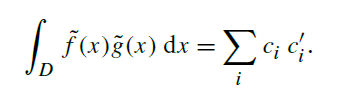
This is an incredibly useful result: the integral of the two functions in the basis can be
found as a simple inner product of their coefficients. Unfortunately, integrals of products
of three or more functions in orthonormal bases aren’t as efficient as products of just
two functions;
(第二个优点,两个函数 乘法的积分,就是等于 他们基函数的系数的简单内积,其实就是
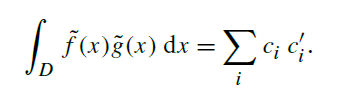 )
)