BP神经网络基础和数学原理

BP神经网络(Back Propagation, 反向传播), 是一种前馈型神经网络. 感知器, BP神经网络, 卷积神经网络和径向基网络都是常见的前馈型神经网络, BP神经网络也是一种多层感知器.

1. 基本概念

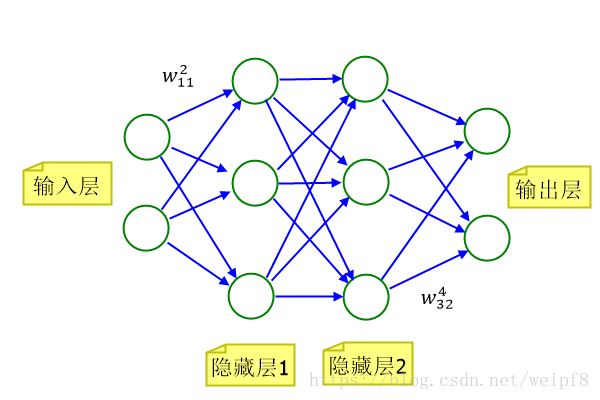
上图是一个简单的BP神经网络结构, 由输入层、隐藏层、输出层组成,其中每个绿色的圆圈是一个神经元, 蓝色的连接线表示数值的传递. 输入层有两个神经元, 表示可以传入一个二维向量, 最终输出一个二维向量. 这个神经网络可以应用于二维平面上样本点的分类, 输入的 2 维向量是点的坐标, 输出的 2 维向量表示分类信息, 例如第一维输出值为 1,第二维输出 0,表示这个点属于第一类, 第一维输出 0, 第二维输出 1, 表示这个点属于第二类. 以其中隐藏层1的第二个神经元为例, 其内部计算过程如下图:

从左向右看, $x_i$ 表示由上一个神经元传入的数值. 权重 $w$ 中, $i$ 表示前一层神经元的序号, $j$ 表示指向的神经元的序号, 上标 $l$ 为层次. 偏置 $b_j$ 是属于这个神经元的, $j$ 表示这个神经元的序号. 经加权求和后得到 $v_j$ , 其中的 $M$ 为前一层的神经元总数. 再将结果代入激活函数 $\varphi$ , 得到 $y_j$ 作为此神经元的输出. (关于激活函数的内容, 请看后文)

2. 公式:

为了公式清晰,省略掉权重 $w$ 的上标 $l$ , 相对于输出层的神经元, 有以下公式:

输入:

$\displaystyle{v}_{{j}}={\sum_{{{i}={1}}}^{{M}}}{w}_{{{i}{j}}}{x}_{{i}}+{b}_{{j}}$

输出:

$\displaystyle{y}_{{j}}=\varphi{\left({v}_{{j}}\right)}$

总误差(Total instantaneous error energy):

$\displaystyle{E}=\frac{1}{{2}}{\sum_{{{j}={1}}}^{{N}}}{\left({d}_{{j}}-{y}_{{j}}\right)}^{2}$

$N$ 表示输出层神经元总数.

其中,总误差函数 $E$ 是优化的目标函数, 通过迭代地改变权重 $w$ 和偏置 $b$ , 使得函数值最小化, 即使得输出结果与输出期望差距缩小.

3. 梯度下降与反向传播算法:

我们的目标是寻找合适的 $w$ 和 $b$ , 使得网络的输出与期望输出尽可能接近, 这样当我们输入一个未经过训练的样本点时, 便可以准确地做出分类. 为了求解, 在训练开始时随时生成 $w$ 和 $b$ , 随机生成的值可以满足均匀分布或者正态分布. 再应用反向传播和梯度下降算法, 不断修正 $w$ 和 $b$ , 使得总误差最小化. 现在, 我们设输出层神经元代号为 $k$ , 隐藏层2 代号为 $j$ , 隐藏层1 代号为 $i$ . 下面分两种情形推导梯度公式.

情形一: 对于输出层神经元

由梯度下降算法, 求得总误差关于权值 $\displaystyle{w}_{{{j}{k}}}$ 的梯度

$\displaystyle\frac{{\partial{E}}}{{\partial{w}_{{{j}{k}}}}}=\frac{{\partial{E}}}{{\partial{y}_{{k}}}}\frac{{\partial{y}_{{k}}}}{{\partial{v}_{{k}}}}\frac{{\partial{v}_{{k}}}}{{\partial{w}_{{{j}{k}}}}}=\frac{{\partial{E}}}{{\partial{v}_{{k}}}}{x}_{{j}}$

同理得到关于偏置 $b_k$ 的梯度

$\displaystyle\frac{{\partial{E}}}{{\partial{b}_{{k}}}}=\frac{{\partial{E}}}{{\partial{y}_{{k}}}}\frac{{\partial{y}_{{k}}}}{{\partial{v}_{{k}}}}\frac{{\partial{v}_{{k}}}}{{\partial{b}_{{k}}}}=\frac{{\partial{E}}}{{\partial{v}_{{k}}}}$

公式推导中我们保留了 $\displaystyle\frac{{\partial{E}}}{{\partial{v}_{{k}}}}$ , 是为了导出局部梯度

$\displaystyle\delta_{{k}}=\frac{{\partial{E}}}{{\partial{v}_{{k}}}}=\frac{{\partial{E}}}{{\partial{y}_{{k}}}}\frac{{\partial{y}_{{k}}}}{{\partial{v}_{{k}}}}=-{\left({d}_{{k}}-{y}_{{k}}\right)}\varphi^{'}{\left({v}_{{k}}\right)}$

关于局部梯度, 我的理解是将一个神经元所有输入的加权和看做一个整体, 权重 $w$ 和 $b$ 仅通过这个整体影响神经网络的其他部分.

则权值调整和偏置的调整分别为

$\displaystyle{\left.\begin{matrix}\Delta{w}_{{{j}{k}}}=-\eta\frac{{\partial{E}}}{{\partial{w}_{{{j}{k}}}}}=-\eta\delta_{{k}}{x}_{{j}}\\\Delta{b}_{{k}}=-\eta\frac{{\partial{E}}}{{\partial{b}_{{k}}}}=-\eta\delta_{{k}}\end{matrix}\right.}$

其中, $\displaystyle\eta$ 是学习率, 或者称为步长, 根据实际情况, 一般取一个较小的数, 如 0.1, 0.01. 前面加个负号意味着沿着负梯度方向(即函数值下降的方向)搜索.

情形二: 对于隐藏层要分一种情况讨论的原因在于无法直接得出隐藏层的误差, 因为只有输出层才有期望的输出, 而隐藏层没有定义. 所以, 对总误差求偏导, 需要穿过输出层, 到达隐藏层, 或者可以理解为原先的复合函数内部又复合了一个函数.

(1) 按照情形一的推导有

$\displaystyle\frac{{\partial{E}}}{{\partial{w}_{{{i}{j}}}}}=\frac{{\partial{E}}}{{\partial{v}_{{k}}}}\frac{{\partial{v}_{{j}}}}{{\partial{w}_{{{i}{j}}}}}=\frac{{\partial{E}}}{{\partial{v}_{{j}}}}{x}_{{i}}$

(2) 根据网络结构图, 可以看出, 隐藏层2 中一个神经元输出值的改变会影响每个输出层神经元的误差, 则对于隐藏层2 的 $\displaystyle\delta_{{j}}$ , 需要由每一个输出层神经元反向传播误差.

$\displaystyle{\left.\begin{matrix}\delta_{{j}}=\frac{{\partial{E}}}{{\partial{v}_{{j}}}}\\={\sum_{{{k}={1}}}^{{N}}}\frac{{\partial{E}}}{{\partial{v}_{{k}}}}\frac{{\partial{v}_{{k}}}}{{\partial{v}_{{j}}}}\\={\sum_{{{k}={1}}}^{{N}}}\delta_{{k}}\frac{{\partial{v}_{{k}}}}{{\partial{v}_{{j}}}}\\={\sum_{{{k}={1}}}^{{N}}}\delta_{{k}}\frac{{\partial{v}_{{k}}}}{{\partial{y}_{{j}}}}\frac{{\partial{y}_{{j}}}}{{\partial{v}_{{j}}}}\\={\sum_{{{k}={1}}}^{{N}}}\delta_{{k}}{w}_{{{k}{j}}}\varphi^{'}{\left({v}_{{j}}\right)}\end{matrix}\right.}$

(3) 得

$\displaystyle{\left.\begin{matrix}\Delta{w}_{{{i}{j}}}=-\eta\frac{{\partial{E}}}{{\partial{w}_{{{i}{j}}}}}=-\eta\delta_{{j}}{x}_{{i}}\\\Delta{b}_{{j}}=-\eta\frac{{\partial{E}}}{{\partial{b}_{{j}}}}=-\eta\delta_{{j}}\end{matrix}\right.}$

可以注意到, 对于不同层的神经元只要求出对应的 $\delta$ 即可, 在后面要讲的卷积神经网络同样沿用这种推到思路.

4. 激活函数

多层的网络结构, 是一种线性变换, 而使用非线性的激活函数, 可以加入非线性因素, 增强模型的表达能力.

Logistic函数:

$\displaystyle\varphi{\left({x}\right)}=\frac{1}{{{1}+{e}^{{-{x}}}}}$

对函数求导得:

$\displaystyle{\left.\begin{matrix}\varphi^{'}{\left({x}\right)}=-\frac{{-{e}^{{-{x}}}}}{{\left({1}+{e}^{{-{x}}}\right)}^{2}}\\=\frac{1}{{{1}+{e}^{ -{{x}}}}}\frac{{e}^{{-{x}}}}{{{1}+{e}^{{-{x}}}}}\\=\frac{1}{{{1}+{e}^{{-{x}}}}}\frac{{{1}+{e}^{{-{x}}}-{1}}}{{{1}+{e}^{{-{x}}}}}\\=\frac{1}{{{1}+{e}^{{-{x}}}}}{\left({1}-\frac{1}{{{1}+{e}^{{-{x}}}}}\right)}\\=\varphi{\left({x}\right)}{\left({1}-\varphi{\left({x}\right)}\right)}\end{matrix}\right.}$

Logistic函数可以将非常大的输入值域映射到 0 到 1 的小范围内. 另外, 可以看到 logistic函数的导数可以用它本身表示, 这便于计算导数. 函数中的 $\displaystyle{e}^{{-{x}}}$ 有时被写为 $\displaystyle{e}^{{-{k}{x}}}$ , 其中 $k$ 为正的常数, 可改变函数曲线的陡峭性.

双曲正切函数:

$\displaystyle \tanh{{\left({x}\right)}}=\frac{{{e}^{x}-{e}^{{-{x}}}}}{{{e}^{x}+{e}^{{-{x}}}}}$

求导得:

$\displaystyle{{\tanh}^{'}{\left({x}\right)}}={1}-{{\tanh}^{2}{\left({x}\right)}}$

Rectifier 函数:

$\displaystyle\varphi{\left({x}\right)}=\max{\left({0},{x}\right)}$

如果一个神经元部署了这个激活函数, 则这个神经元被称为 ReLU (rectified linear unit).

有时也使用一个平滑的 softplus 函数逼近 Rectifier 函数.

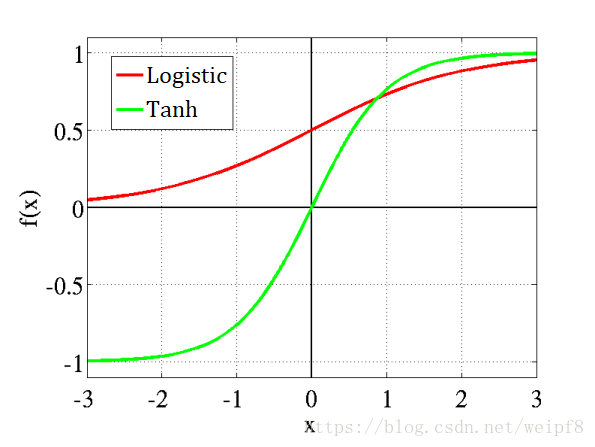
$\displaystyle\varphi{\left({x}\right)}= \ln{{\left({1}+{e}^{x}\right)}}$

这两个函数的图像:

5. 误差函数

从上图中可以发现, 当 $x$ 变大或变小时, 曲线趋于平缓, 即梯度变小, 由导出的公式可以看出, 即使有较大的误差, 也会使得 $\displaystyle\Delta{w}$ , $\displaystyle\Delta{b}$ 很小, 这会导致权重 $w$ 和偏置 $b$ 更新缓慢. 这个问题源于我们选择的误差函数是方差代价函数. 即

$\displaystyle{E}_{{j}}=\frac{1}{{2}}{\left({d}_{{j}}-{y}_{{j}}\right)}^{2}$

为了解决上面遇到的问题, 引入交叉熵代价函数(Cross-entropy cost function), 应用于输出层, 原有的激活函数可保留下来.

交叉熵代价函数:

$\displaystyle{C}=-{\sum_{{{j}={1}}}^{{N}}}{\left({d}_{{j}}{ \ln{{y}}_{{j}}+}{\left({1}-{d}_{{j}}\right)} \ln{{\left({1}-{y}_{{j}}\right)}}\right)}$

按照前面的推导过程, 以情形一为例, 推导出代价函数 $C$ 关于 $w_{ij}$ 的偏导数:

$\displaystyle{\left.\begin{matrix}\frac{{\partial{C}}}{{\partial{w}_{{{i}{j}}}}}=\frac{{\partial{C}}}{{\partial{y}_{{j}}}}\frac{{\partial{y}_{{j}}}}{{\partial{v}_{{j}}}}\frac{{\partial{v}_{{j}}}}{{\partial{w}_{{{i}{j}}}}}\\=-{\sum_{{{j}={1}}}^{{N}}}{\left(\frac{{d}_{{j}}}{{y}_{{j}}}-\frac{{{1}-{d}_{{j}}}}{{{1}-{y}_{{j}}}}\right)}{{y}_{{j}}^{'}}{y}_{{i}}\\=-{\sum_{{{j}={1}}}^{{N}}}\frac{{{d}_{{j}}{\left({1}-{y}_{{j}}\right)}-{\left({1}-{d}_{{j}}\right)}{y}_{{j}}}}{{{y}_{{j}}{\left({1}-{y}_{{j}}\right)}}}{y}_{{j}}{\left({1}-{y}_{{j}}\right)}{y}_{{i}}\\=-{\sum_{{{j}={1}}}^{{N}}}{\left({d}_{{j}}-{y}_{{j}}\right)}{y}_{{i}}\end{matrix}\right.}$

结果中不包含激活函数 $y_j$ 的导数, 而是期望值与激活函数值的差, 则当误差大时, 权重更新快, 误差小时, 权重更新慢, 这是我们期望达到的效果.

另外, 对于一个多分类的问题, 我们希望输出的结果可以被视为属于某一类的概率, 即将输出向量转换后, 使得各维度和为 1. 这里引入 Softmax函数, 或者叫归一化指数函数(Normalized exponential function):

$\displaystyle\sigma{\left({z}\right)}_{{i}}=\frac{{e}^{{{z}_{{i}}}}}{{{\sum_{{{j}={1}}}^{{N}}}{e}^{{{z}_{{j}}}}}},{i}={1},\ldots,{N}$

其中, $z$ 是一个 $N$ 维的向量. 函数值是向量中每一维归一化后的值.

6. 反向传播和梯度下降算法进一步讨论

(1) 反向传播算法实现了一种对可能的权重空间的梯度下降搜索, 它迭代地减小网络输出值和期望值的差距. 对于多层的网络, 误差函数可能有多个局部极小值, 梯度下降算法可能会陷入某个局部极小值, 而不能保证达到全局最小. 但是在实际应用中, 人们发现这些局部极小值仍然可以较好地符合期望. 可以这样直观的理解这个问题: 由于多层的网络含有很多的权重, 即函数的维度很高, 当陷入一个局部极小值时, 对于其它的权重, 这未必是局部极小值(因为关于某个权重的偏导数与其他权重无关), 而有可能离开这个局部极小值.

(2) 在实际应用中, 训练一个 BP 神经网络有两种方式: 一是在线学习, 即随机梯度下降算法(SGD), 方法是一次输入一个样本点, 计算出总误差, 运用反向传播算法, 调整权重和偏置. 二是批量学习, 即批梯度下降算法, 方法是先后输入多个样本点, 累计输出的总误差, 最后求出每个数据的总误差平均值, 以这个平均值, 运用反向传播算法, 调整权重和偏置. 每次输入的多个数据叫做 batch(一批), 数据的数目叫做 batch的大小, 每进行一次这样的过程叫做一个epoch. 下面对比来看这两种方法:

a. 随机梯度下降: 对每个样本点做一次反向传播, 由于对单个样本点来说, 它在空间中的分布具有不确定性, 所以梯度的搜索方向具有一定的随机性, 从而不容易陷入局部极小值. 其次, 它能够追踪到训练数据很小的改变, 尤其是数据产生于不稳定的环境下.

b. 批梯度下降: 由于一次对一批样本点的学习, 在简单的情况下, 能够相对较快地到达局部极小值. 从统计的角度来看, 批梯度下降可以看成某种形式的统计推断(个人理解为中心极限定理), 适合于解非线性回归问题.

(3) 避免局部最小值的启发式方法:

a. 对权重的更新增加一个冲量项. 即分别在 $\displaystyle\Delta{w}$ $\displaystyle\Delta{b}$ 两式后面加一项 $\displaystyle\alpha\Delta{w}_{{{i}{j}}}{\left({n}-{1}\right)}$ , $n-1$ 表示上一次迭代时的调整量, $\alpha$ 称为冲量常数, 加上这一项后, 相当于增加下一次权重调整的步长, 从而可能一次越过某一局部极小值, 到达下一个更小的极小值.

b. 使用同样的数据训练多个网络, 但用不同的初始化方法初始化权重. 选出最优的训练结果. 或者保留训练出来的多个网络模型, 在进行预测时, 计算多个网络的加权平均值做为最终的结果.

7. 应用举例:

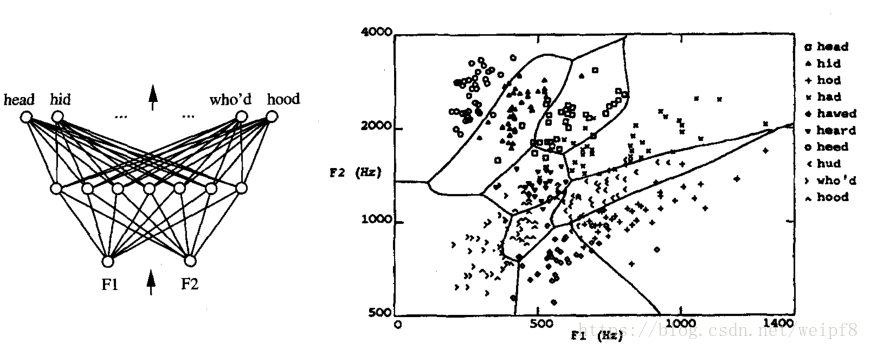
首先, 由左边的神经网络结构图可以看出, 输入一个 2 维的向量, 经过一个隐藏层, 输出 10 维的向量. 这个网络学习一个语音识别的模型. 首先根据单词发音的声波, 进行频谱分析(快速傅里叶变换), 选出两个振幅最大的频率, 作为输入向量, 右图是将输入向量映射到二维平面的结果, 经过学习, 可以得到一个复杂的非线性分类平面.

建议查看原文获得更好的阅读体验！

[阅读原文]