基础的BP神经网络

基础的BP神经网络 ——— **算法简介** 神经网络中最基本的单元就是神经元模型。神经元模型有多个输入，只有一个输出，神经元接受这多个输入，并对其做出响应。如图所示：

$\ x_1,x_2,x_3$ 都是这个神经元的输入，假设输出表示为y，那么 $\ y=f(x_1,x_2,x_3)$ ，这里f表示一个激活函数，最常见的激活函数就是之前学习的 $\ Sigmoid$ 函数: $\ Sigmoid(x)= \frac{1}{1+e^{-x} }$ 。把很多个这样的神经元按照一个组织结构排列起来互相连接就构成了神经网络的模型。
最简单的神经网络就是单层感知机，只有输入层和输出层两个层面。更复杂、有效的模型是多层网络—包含一个或者多个隐藏层。对应的学习算法就是误差逆向传播算法（BP算法）。
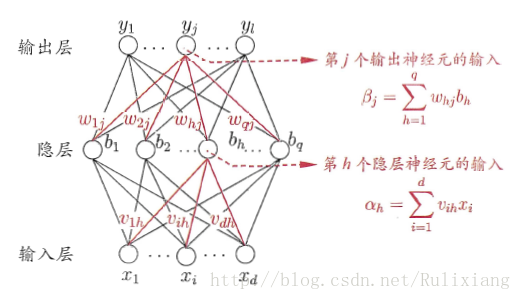
给定训练集 $\ D={(x_1,y_1 ),(x_2,y_2 ),…,(x_m,y_m )},x_i∈R^d,y_i∈R^l，$ 假设有一个三层（仅包含一个隐含层）的神经网络模型：

隐含层和输出层都是用sigmoid函数。输入神经元共d个，另外有l个输出神经元和q个隐含层神经元。其中输出层第j个神经元的阈值用 $\ θ_j$ 表示，隐含层第h个神经元的权值为 $\ γ_h$ 。输入层第i个神经元和隐含层第h个神经元之间的连接权值为 $\ v_{ih}$ ，隐含层第h个神经元与输出层第j个神经元之间的连接权值 $\ w_{hj}$ ；记隐含层第h个神经元接收到的输入为 $\ α_h=\sum\limits_{i=1} ^{d}(v_{ih}x_i)$ ，输出层第j个神经元接收到的输入为 $\ β_h=\sum\limits_{h=1} ^{q}(w_{hj}b_h)$ , 其中 $\ b_h$ 是隐含层第h个神经元的输出。对于训练例 $\ (x_k,y_k)$ ，假设神经网络的输出为: $\ Y_k=(Y_1^k,Y_2^k,……Y_l^k)，$ 即：

Y k j = f (β j - θ j)

$\ Y_j^k=f(β_j-θ_j)$
神经网络在训练样本

(xk,yk) $\ (x_k,y_k)$ 上的均方误差为

Ek=12∑j=1l(Ykj−ykj)2 $\ E_k=\frac{1}{2} \sum\limits _{j=1}^{l}(Y_j^k-y_j^k )^2$ .BP算法基于梯度下降的策略，以目标的负梯度方向对参数进行调整，对于误差

Ek $\ E_k$ ，给定学习速率η, 对于权重值w，有：

∆ w h j = - ( η \cdot \partial E k ) ( \partial w h j )

$\ ∆w_{hj}=\frac{-(η·∂E_k)}{(∂w_{hj} )}$
根据网络结构：

( \partial E k ) ( \partial w h j ) = ( \partial E k ) ( \partial Y k j ) ( \partial Y k j ) ( \partial β j ) ( \partial β j ) ( \partial w h j )

$\ \frac{(∂E_k)}{(∂w_{hj} )}=\frac{(∂E_k)}{(∂Y_j^k )}\frac { (∂Y_j^k)}{(∂β_j ) }\frac{(∂β_j)}{(∂w_{hj} )}$
根据

βj $\ β_j$ 的定义，显然有：

(∂βj)(∂whj)=bh $\ \frac{(∂β_j)}{(∂w_{hj} )}=b_h$ 。根据

Sigmoid $\ Sigmoid$ 函数的性质

f′(x)=f(x)(1−f(x)) $\ f'{ (x)}=f(x)(1-f(x))$ ，有：

g j = - ( \partial E k ) ( \partial Y k j ) ( \partial Y k j ) ( \partial β j ) = - (Y k j - y k j) f' (β j - θ j) = Y k j (1 - Y k j) (Y k j - y k j)

$\ g_j=-\frac{(∂E_k)}{(∂Y_j^k )} \frac{(∂Y_j^k)}{(∂β_j )}=-(Y_j^k-y_j^k ) f' (β_j-θ_j )=Y_j^k (1-Y_j^k )(Y_j^k-y_j^k)$
和上面的式子结合，得到BP算法中关于

wij $\ w_ij$ 的更新公式

∆whj=ηgjbh. $\ ∆w_{hj}=ηg_j b_h.$ 类似的方法可以得到:

∆ θ j = - η g j,

$\ ∆θ_j=-ηg_j,$

∆ v i h = η e h x i,

$\ ∆v_ih=ηe_h x_i,$

∆ γ h = - η e h

$\ ∆γ_h=-ηe_h$ 。其中的

eh $\ e_h$ 的具体值为：

e h = ( \partial E k ) ( \partial b h ) ( \partial b h ) ( \partial α h )

$\ e_h=\frac {(∂E_k)}{(∂b_h ) } \frac{(∂b_h)}{(∂α_h )}$

= - \sum j = 1 l ( \partial E k ) ( \partial β j ) ( \partial β j ) ( \partial b h ) f' (α h - γ h)

$\ =-\sum\limits_{j=1}^{l}\frac{(∂E_k)}{(∂β_j ) }\frac{ (∂β_j)}{(∂b_h ) }f'(α_h-γ_h)$

= \sum j = 1 l w h j g j f' (α h - γ h) = b h (1 - b h) \sum j = 1 l w h j g j

$\ = \sum\limits_{j=1}^{l}{w_{hj} g_j }f' (α_h-γ_h )=b_h (1-b_h)\sum\limits_{j=1}^l{w_{hj} g_j}$
BP算法的具体执行步骤：先将输入实例提供给输入层神经元，然后将信号前传，知道产生输出层的结果，然后计算输出层的误差；再将误差逆向传播到隐含层神经元，最后根据隐含层神经元的误差和连接权的阈值进行调整。这个过程循环进行，直到达到停止条件为止。

实验：

在MATLAB下完成了这次相关的试验，用了MATLAB下神经网络的相关函数和使用了UCI的IRIS数据集，随机选择其中的20%作为测试集，其余的作为训练集。得到训练结果表示如图：

神经网络迭代过程中的均方误差变化，可以看到200个epoch之后MSE基本保持不变了，在748个epoch时均方误差达到最小，迭代停止。
实验的数据量较小，所以重复进行了20次，每次分类的准确率：

平均准确率为0.9933，是非常不错的结果。

结论：
基本的BP神经网络的过程还是比较简明的，更复杂的网络结构也基本上是同理。这里实现的也是最基础的网络结构，得到的分类结果也是比较优秀的，当然这里的数据集也是比较简单的。

基础的BP神经网络

猜你喜欢